さてさて、以前OpenAIの『DALL-E』のブログをもとに、モデルを想像しながら解説しましたが、もう既に論文が出ていますので、今回はきちんと論文に沿って解説をしていきたいと思います。
『DALL-E』は文章を与えると、それに沿った様々な画像が生成される非常に面白いモデルです。
例えば、こちらは“森に住むカピバラのX線写真”を与えたときに生成された画像です。

ブログの解説の方にはDALL-Eという名前の由来の説明や色々な画像を生成した例を載せていますので、そちらもご参考にしていただければと思います。
また、VQ-VAEを理解しておくと、こちらも理解しやすくなると思いますので、VQ-VAEの記事も参考にしていただければと思います。
「DALL-E」からさらに進化した「DALL-E2」のベータ版が公開されており、そちらを使った画像生成結果を以下の記事で紹介しています。
ご興味のある方は、どんなことができるかやそのクオリティを確認していただければと思います。
では、早速以下の論文をもとに見ていきましょう。
論文はこちらです。
『Zero-Shot Text-to-Image Generation』
目次
DALL-Eとは
『DALL-E』はテキスト情報を画像を生成する“text-to-image generation”のモデルです。
以下が実際にテキストから画像を生成した例です。

例えば、(a)だと、
アコーディオンから作られたバク。アコーディオンの模様をしたバク。
というテキスト情報から生成された例です。
恐らく学習データに“アコーディオンから作られたバク”というキャプションや画像はないと思いますが、うまくできていますね。
(b)は、
犬を散歩するクリスマスセーターを着た赤ちゃんハリネズミのイラスト。
です。
(c)は、
「backprop」と書かれたネオンサイン。「backprop」と読むネオンサイン。バックプロップ・ネオンサイン。
です。
さすがにこんな画像は実在しないでしょうね。
しかし、うまくできています。
(d)は2つの画像を生成していて、
上とまったく同じ猫のスケッチが下にある。
というテキスト情報を与えています。
面白いですね。
当初の発想は、GPTのように、“より大きなモデルで大量のデータを学習”させれば、従来のモデルよりももっと良いモデルが作れるだろうということでしたが、想定していた以上に様々な画像を生成できたとのことです。
では、どうやってこの画像を生成しているかについて、次から解説していきたいと思います。
DALL-Eの仕組み
全体的な仕組みはVQ-VAE、もしくはその後続のVQ-VAE2で行われていたこととあまり変わりません。
VQ-VAEは、画像をインプットして、離散的な潜在変数に圧縮し、それを復元するオート・エンコーダです。
DALL-Eでは、同様にVQ-VAEを使って256x256xRGBの画像を32x32の潜在変数に圧縮します。
そして、キャプションであるテキスト情報とその32x32の画像の潜在変数をTransformerに学習させます。
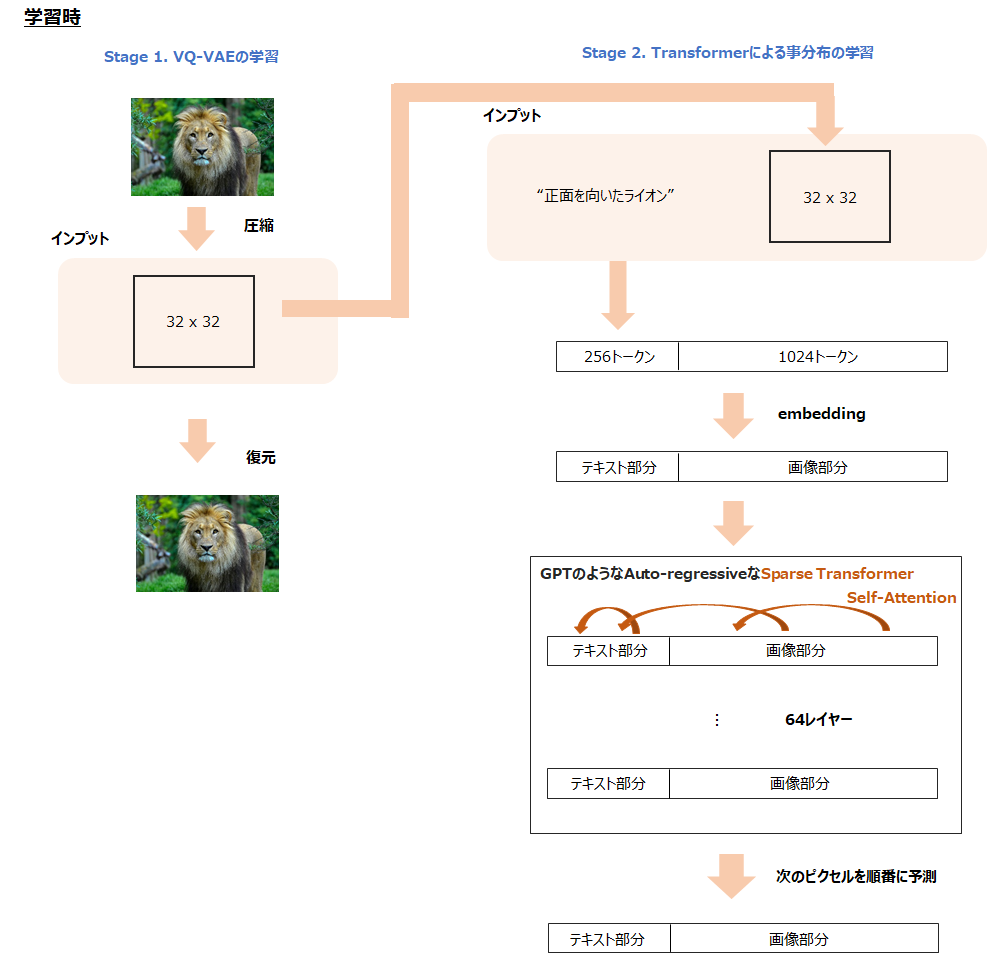
DALL-EではTransformerの優位性を全面的に利用します。
Transformerは自然言語処理ではBERTやGPT-3に使われ、最近では画像分野でもVision Transformer(ViT)、DETR(Detection with Transformers)といったモデルで使われており、CNNに取って代わりそうな勢いのある仕組みです。
Transformerの重要な特徴として、Inductive Bias(モデルの仮定)が少ないことから、特に大量のデータが利用できる場合に他のモデルよりも力を発揮することが可能です。
そこで、学習データ量を増やして巨大なモデルを学習します。
GPT-3やCLIPでも見られましたが、学習データを増やして巨大なモデルを学習させることで、特定のデータセットに偏るのではなく、汎化されることがわかっています。
その考え方を踏襲して、DALL-Eでは2億5000万の画像-テキストのペアのサンプルを使って、120億のパラメータを持つTransformerモデルを学習させます。
画像の生成時には、キャプションであるテキスト情報を学習済みのTransformerに与え、32x32の潜在変数\(z\)を生成し、その潜在変数からVQ-VAEを使って画像を生成する(復元する)といった手順です。
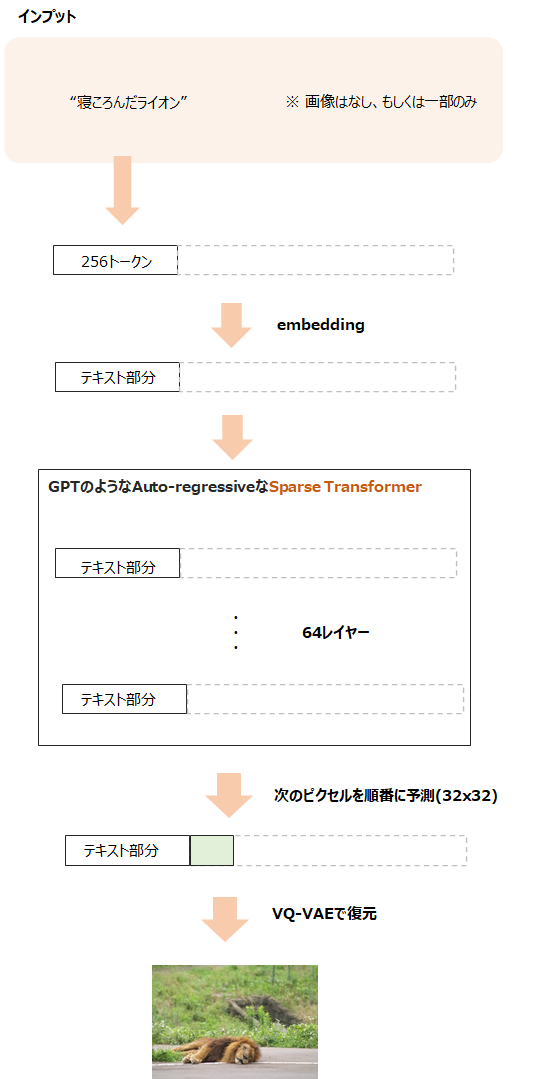
では、モデルの詳細を見ていきましょう。
モデルの詳細
全体的な仕組みはTransformerというよりも、VQ-VAEと言えるのではないかと思います。
論文では、VQ-VAEと言わず“dVAE”と呼んでいます。
DALL-Eの仕組みを理解するにはVQ-VAEを理解するのが早いですので、簡単にVQ-VAEをおさらいしたいと思います。
ご存じの方は飛ばしていただいて大丈夫です。
VQ-VAEの概要
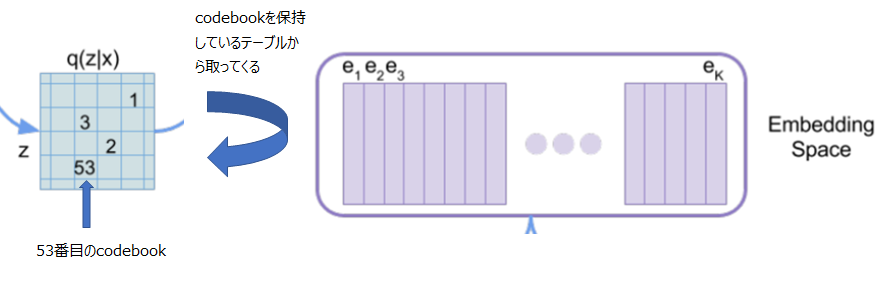
VQ-VAEは潜在変数を使ったオート・エンコーダですが、潜在変数\(z\)を離散的なベクトルで表現します。
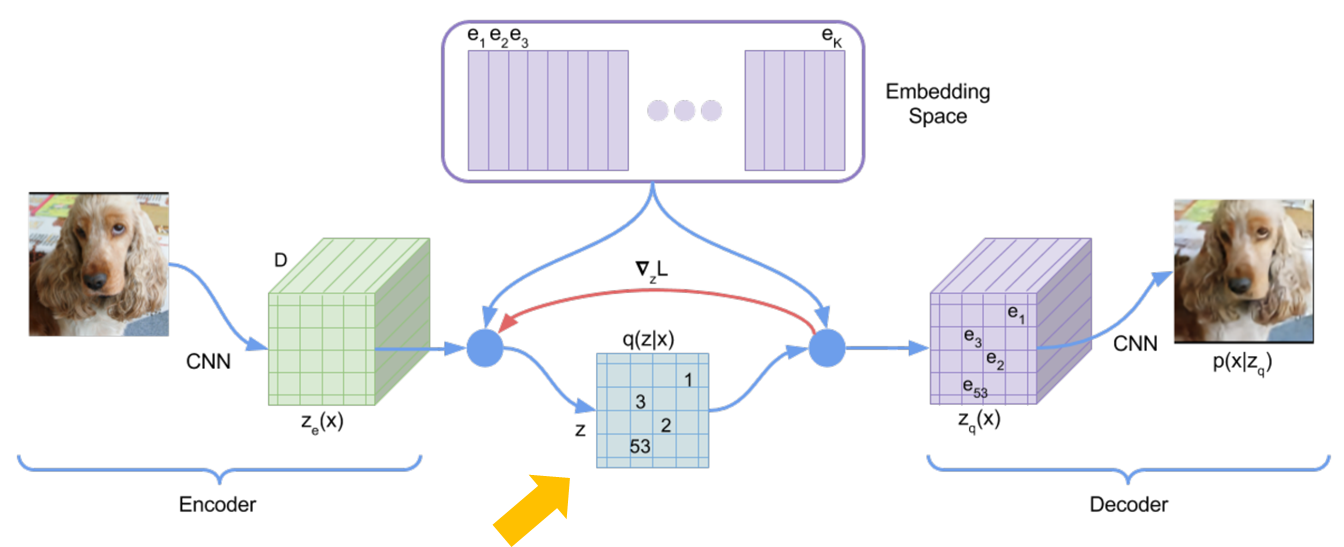
上の図のオレンジの矢印で指した部分が潜在変数になります。
この潜在変数は、1や53といった数値が記載されていますが、これはEmbedding Spaceにある離散的な埋め込み表現(Code book)のうちの1番目や53番目のベクトルを使うということです。

このような仕組みでオート・エンコーダを学習させるというものです。
そして、VQ-VAEの学習時には潜在変数の事前分布\(p(z)\)を一様分布としているのですが、実際に画像を生成するときには一様分布ではなく、PixelCNNというモデルにVQ-VAEのエンコーダが出力する\(z\)の分布を学習させ、PixelCNNを使って\(z\)を生成し、デコーダが新しい画像を生成させるという仕組みです。
DALL-Eでは、PixelCNNの代わりにTransformerを使います。
PixelCNNについてはこちらをご参照ください。
DALL-Eの全体像
では、DALL-Eに戻りましょう。
DALL-Eの学習も同じ方法で、2つのステージから構成されます。
- Stage 1
もとの256x256x3(RGB)の画像に対して、32x32に圧縮するためにVQ-VAEを学習させます(論文ではdVAE(discrete VAE)と呼んでいます)。
codebookの種類は8192とします。 - Stage 2
\(z\)の事前分布をPixelCNNではなく、より汎用性の高いTransformerを使って学習させます。
DALL-Eでは、潜在変数は圧縮した画像\(z\)(ここではimage tokenと呼んでいます)と文字情報になりますので、この同時分布をTransformerで学習します。
数式で確認
では、数式でモデルを確認しましょう。
まず、インプットとなる画像を\(x\)、キャプションを\(y\)、画像の潜在変数を\(z\)とします。
そして、潜在変数を含めたこの3つの同時分布\(p_{\theta, \psi} (x,y,z)\)を考えます。
この同時分布は、以下のように潜在変数から画像が生成される部分\(p_\theta\)と潜在変数の分布\(p_\psi(y, z)\)に分解することができます。
$$p_{\theta, \psi} (x,y,z)=p_\theta(x|y, z)p_\psi(y,z)$$
そして、変分推論の考え方により、
$$\begin{align}
p_{\theta, \psi}(x,y)\ge \mathbb{E}_{z\sim q_\phi(z|x)}&(\ln p_\theta(x|y,z)- \\
&\beta D_\text{KL}\left(q_\phi(y,z|x),p_\psi(y,z)\right)
\end{align}$$
と表されます(VAEのELBを求めているだけなので雰囲気はわかるのですが、\(q_\phi(z|x)\)と\(q_\phi(y, z|x)\)が混在していたりして、きちんと導出しようとするとよくわかりませんでした、お分かりの方は教えていただければ嬉しいです。)。
つまり、左辺の対数尤度は右辺よりも必ず等しいか大きくなり、右辺は変分下界(Evidence Lower Bound; ELB)と呼ばれます。
尤度ではなく、このELBを最大化しようというのが変分推論です。
詳細はVAEの記事で解説しているので、こちらもご参照ください。
この\(\beta\)はもともとの変分推論にはないパラメータですが、β-VAEというVAEの亜種で提案されたものです。
\(\beta=1\)のときが厳密な下界ですが、\(\beta\)をある程度大きくした方がうまくいくようです。
式・パラメータの解釈
さて、\(\phi\)、\(\psi\)、\(\theta\)というパラメータが出てきました。
\(q_\phi(y,z|x)\)というのは、\(y, z\)の同時分布の事後分布になります。
つまり、データ\(x\)を観測した場合の、\(y,z\)の分布です。
ですので、\(\phi\)は\(x\)を与えたときの事後分布のパラメータですので、オート・エンコーダの枠組みではエンコーダのパラメータということになります。
\(p_\theta(x|y,z)\)は、画像の潜在変数\(z\)が与えられたときの画像\(x\)の分布です。
ですので、\(\theta\)は潜在変数から画像を復元する際に使用するパラメータ、つまりデコーダのパラメータになります。
最後に\(p_\psi\)ですが、こちらは潜在変数の事前分布になります。
これはTransformerによりモデル化されます。
DALL-Eの詳細
では、Stage 1とStage 2を細かく見ていきます。
Stage 1:画像の潜在変数の学習
まずは、画像の潜在変数に学習するオート・エンコーダの部分です。
繰り返しになりますが、以下の式で表されるELBを最大化するように学習します。
$$\begin{align}
p_{\theta, \psi}(x,y)\ge \mathbb{E}_{z\sim q_\phi(z|x)}&(\ln p_\theta(x|y,z)- \\
&\beta D_\text{KL}\left(q_\phi(y,z|x),p_\psi(y,z)\right)
\end{align}$$
ここで学習するパラメータはデコーダのパラメータ\(\theta\)とエンコーダのパラメータ\(\phi\)です。
事前分布のパラメータ\(\psi\)は学習せず、これはStage 2で学習します。
事前分布が決まらないと下界の最大化はできないじゃないか!となりますが、事前分布はここではいったん一様分布とします。
離散的な値を取るので、すべての確率が同じであるカテゴリ分布となります。
離散的なベクトルをcodebookと呼びますが、このcodebookの種類は\(K=8192\)とします。
まず、256x256x3の画像をいくつかの畳み込み層で32x32x\(d\)次元に落とします(詳細は論文、もしくはこちらのコードをご参照ください)。
これを\(z_e\in \mathbb{R}^{32\times 32\times d}\)としましょう。
この\(d\)はcodebookの次元に合わせます。
そして、各ピクセル\(z_{i,j}\in \mathbb{R}^{d}\)と埋め込み空間にあるcodebookと最も距離が近いcodebookを選びます。
$$k=\arg \min_{k}\| e_k - z_{i, j}\|_2$$
そして、デコーダへのインプットは
$$z_q=e_k$$
とします。
さて、ここで学習時の問題が出てきます。
上のようにargminを取ってしまうと、微分ができないため勾配が計算できず、学習することができません。
VQ-VAEではこの問題をstraight estimatorと呼ばれる方法で回避しています。
straight estimatorは単純に損失関数\(L\)の\(z_e\)による微分を\(L\)の\(z_q\)による微分で置き換えるものです。
ようは、本来は\(\partial L/ \partial z_e\)を計算しないといけないのですが、\(\partial L/ \partial z_q\)をそのまま流してしまおうというものです。
一方で、DALL-Eではstraight estimatorは使わず、Gumbel-softmax relaxation(もしくはConcrete distribution)という手法を使います。
Gumbel-softmax relaxationを簡単に言うと、1点のみを取るargmaxを少し緩めてsoftmaxの形にしてやるというものです。
これにより、微分をすることが可能になります。
以下のようなイメージです。
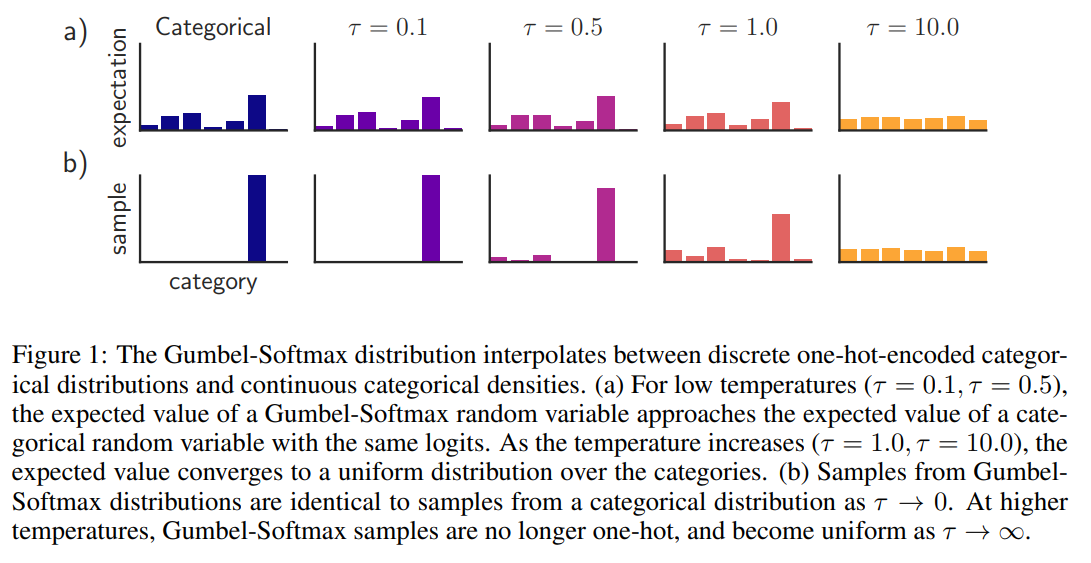
WITH GUMBEL-SOFTMAX」(https://arxiv.org/abs/1611.01144)
一番左がargmaxを取る場合の実際のカテゴリカル分布の期待値とサンプルになります。
b)のサンプルの例ではカテゴリの中から一つ選ぶので一つだけ棒が立っています。
Gumbel-softmax relaxationでは、\(\tau\)というパラメータを使ってこれがゼロに近いとargmaxになり、大きくすると緩まっていきます。
例えば、本来のカテゴリ分布からのサンプリングを\(\tau=0.5\)の場合のようなsoftmaxで近似しようというものです。
詳細は割愛しますが、\(\tau\)は学習当初は大きめの値に設定し、徐々に小さくして1/16にするなどの工夫を行っています。
ようは、初めはargmaxをざっくり近似して、学習が進んでいくとより実際のargmaxに近づけていくというものです。
他にも、\(\beta\)は段々大きくしていき、最終的には6.6になるように設定しています。
少しずつKLダイバージェンス項のペナルティを大きくしていくイメージですね。
他にも論文には細かい工夫が記載されていますので、気になる方は論文をご参照ください。
Stage 2:事前分布の学習
このStage 2では、テキスト\(y\)と圧縮した画像\(z\)の事前分布\(q_\psi(y, z)\)を学習します。
Stage 1でオート・エンコーダはもう学習済みですので、\(\theta\)、\(\phi\)は固定します。
\(p_\psi\)はパラメータが120億個のTransformerを使います。
特に、“Attention is All You Need”で提案されたTransformerに対して、より長い文章でも対応できるようにしたSparse Transformerを使用します。
Sparse Transfomerの詳細はこちらをご参照ください。
DALL-Eでは、以下のような(a)の行に対するattentionマスク、(b)のような列に対するattentionマスク(と計算効率を良くするために変形した(c))、(d)の畳み込みattentionマスクの3種類を使います。

そして、Sparse Transformerへのインプットはテキストの文字列256語と圧縮した画像の32x32の1024個を連結したものです。

テキストのボキャブラリ数は16,384語で、画像の方のボキャブラリ数は8192語になります。
画像については、ボキャブラリ?と思うかもしれませんが、ようは離散的に表現された画像をテキストのように扱っていて、1024語がそれぞれ単語列で、それらの単語の埋め込み表現が対応するcodebookになるイメージです。
これで、画像情報についても自然言語のように扱うことが可能になりました。
インプットの長さが256+1024の1280個になり、TransformerではAttentionの計算部分で結構処理が重くなるレベルです。
ですので、Sparse Transformerを使っています。
また、attentionの仕方も工夫がされており、以下の3パターンのattentionを使っていまうす。
- テキストからテキストへのattention
- 画像から画像へのattention
- 画像からテキストへのattention
最終的には、テキストから圧縮した画像をTransformerで生成するので、テキストから画像へのattentionはありあません。
なお、レイヤ数は64です。
損失関数はクロス・エントロピー誤差を使いますが、テキストと画像部分に分けて、テキストの方は1/8し、画像の方は7/8とします。
これは、最終的には画像を生成するので、テキストよりも画像の方の損失を重視するためです。
データの収集
では、巨大なデータセットの作成方法について簡単に説明します。
インターネットから収集した2億5千万のテキスト-画像ペアを使います。
ただし、インターネットから画像を収集することはできますが、キャプションがありません。
そこで、GoogleのConceptual Captionsを参考にキャプションを作成します。
まずConceptual Captionsの前処理は以下のようなものです。
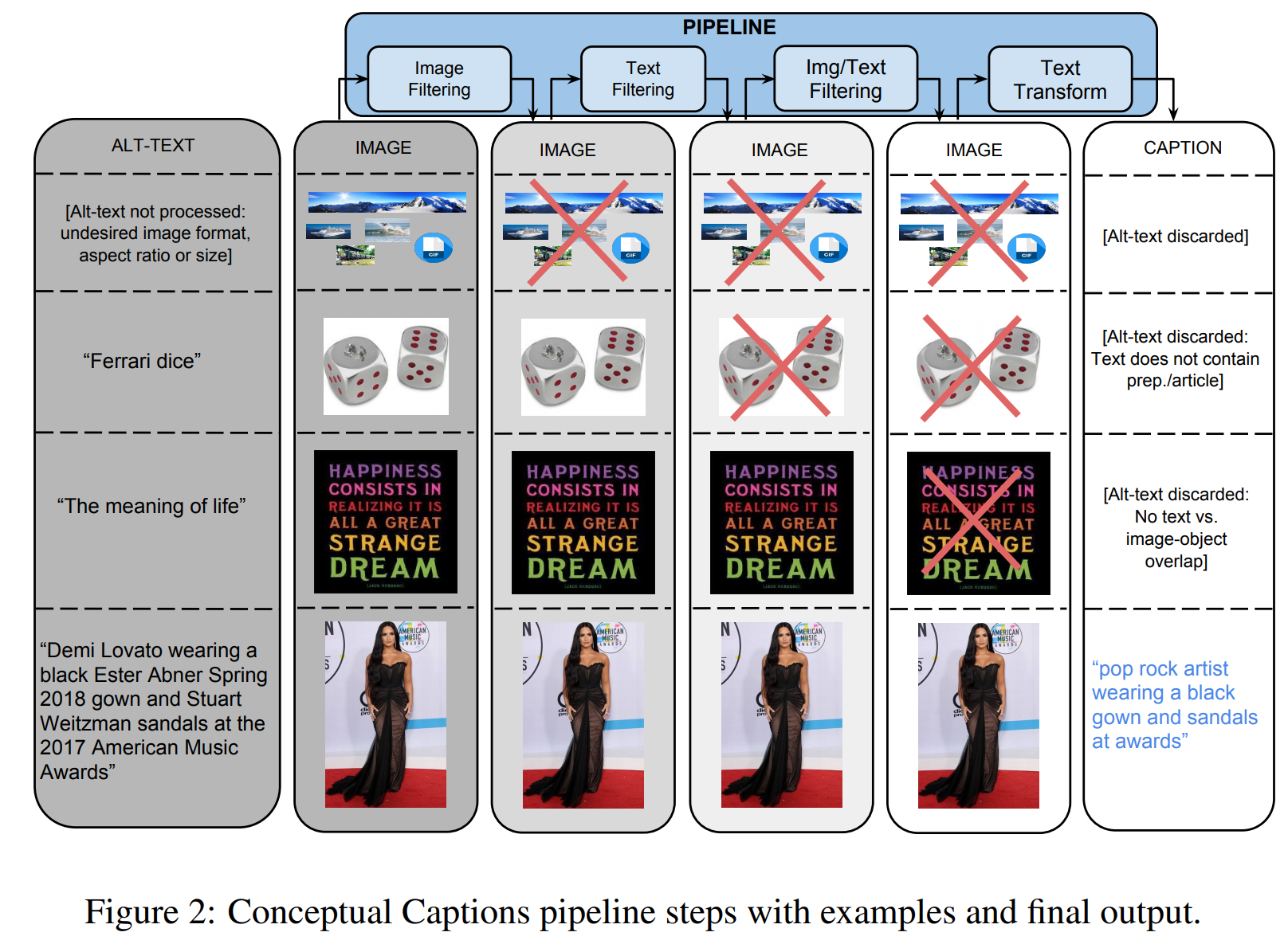
画像とHTMLのAlt-Textを使って判定します。
1段目は、画像の判定で、サイズやファイルフォーマット(JPEGのみを使う)によってフィルタリングされています。
DALL-Eのデータセットにおいても、アスペクト比が\([1/2, 2]\)に入っていないものは除いています。
2段目は、テキストの判定で、Alt-Textが短いため除かれています。
DALL-Eでも英語でないものは除いています。
3段目は、テキストと画像の判定で、画像とテキストの意味が重なっていないので除かれています。
これらのフィルタリングを経て、最終的に残ったのが4段目の画像になります。
DALL-Eにおいてもこのようなフィルタリングを行い、最終的に2億5000万個のサンプルが出来ています。
このデータセットはConceptual Captionsのデータを含んでおり、YFCC100Mというデータセットの一部を含んでいます。
サンプル画像の生成
サンプル画像の生成自体は、テキストをインプットとして、Transformerで32x32の画像の潜在変数を生成し、dVAEで最終的な画像を生成することが可能です。
DALL-Eではさらに、そこから画像とテキストのモデルである「CLIP」を使って、1つのテキストについて生成された複数の画像を、ランキングし、上位の画像を出力するという方法を使います。
CLIPについては、こちらをご参照ください。
ここでは、候補となる画像の数を\(N=512\)とし、そのうちから上位\(k\)個の画像を選びます。
実験
では、構築したモデルで実験した結果を見ていきましょう。
MS-COCOデータセットを使ってDF-GAN、DM-GAN、AttnGANと比較していきます。
まずは、生成例を比較しましょう。

例えば、右から3番目の“面白い顔をしている可愛いキリン”の生成画像を見ると、DALL-Eの方がうまく生成できていますね。
他を見ても、DALL-Eの方が良さそうです。
続いて、人の目によりDALL-EとDF-GANを比較します。
以下のような感じで、どっちがより現実の画像に近いか?、どっちがキャプションと合っているか?を答えてもらいます。

各画像について、5人に回答してもらいます。
それを集計した結果が以下のようになっています。
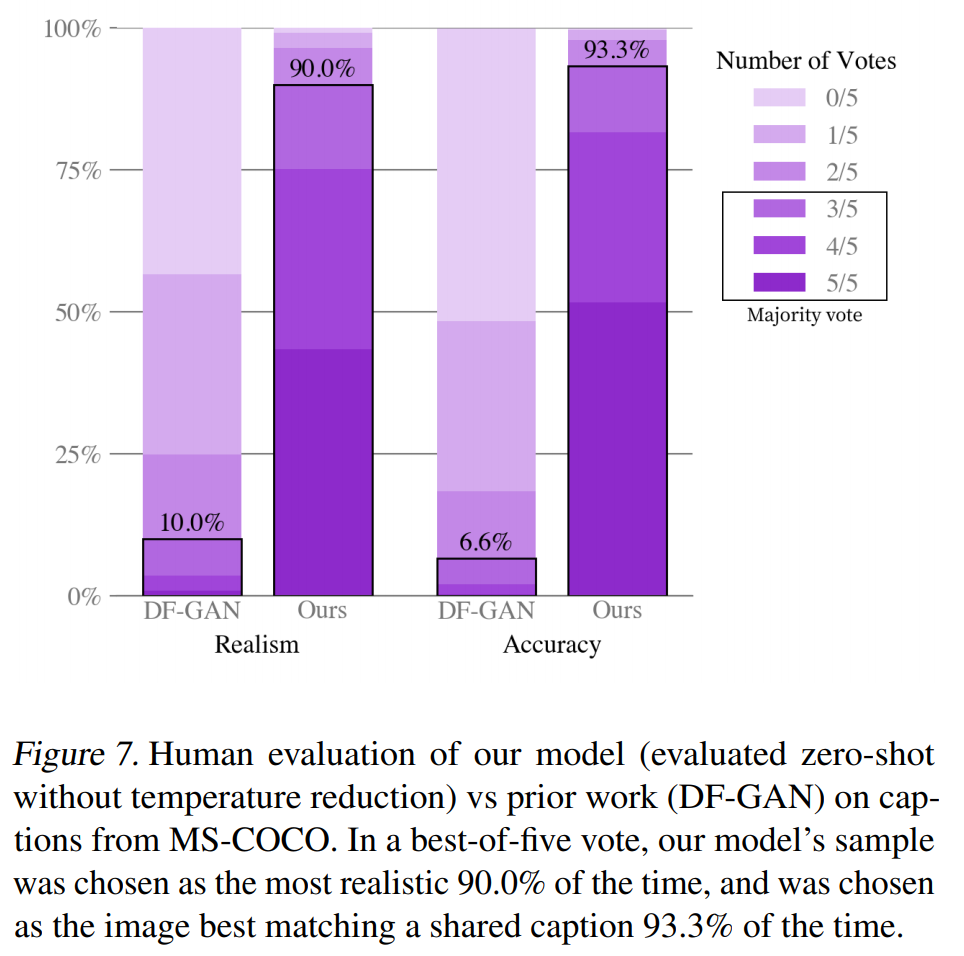
左側のRealismを見ると、半分(3人)以上の人がDALL-Eの方が本物に近いと答えた画像の割合は90%にも上ります。
また、右側のAccuracyを見ると、半分以上の人がDALL-Eの方がキャプションと合っていると答えた画像の割合は93.3%になっています。
人の目で見た評価でもDALL-Eの方が良いようです。
続いて、上記のモデルとFID(Frechet Inception Distance)、IS(Inception Score)を比較します。
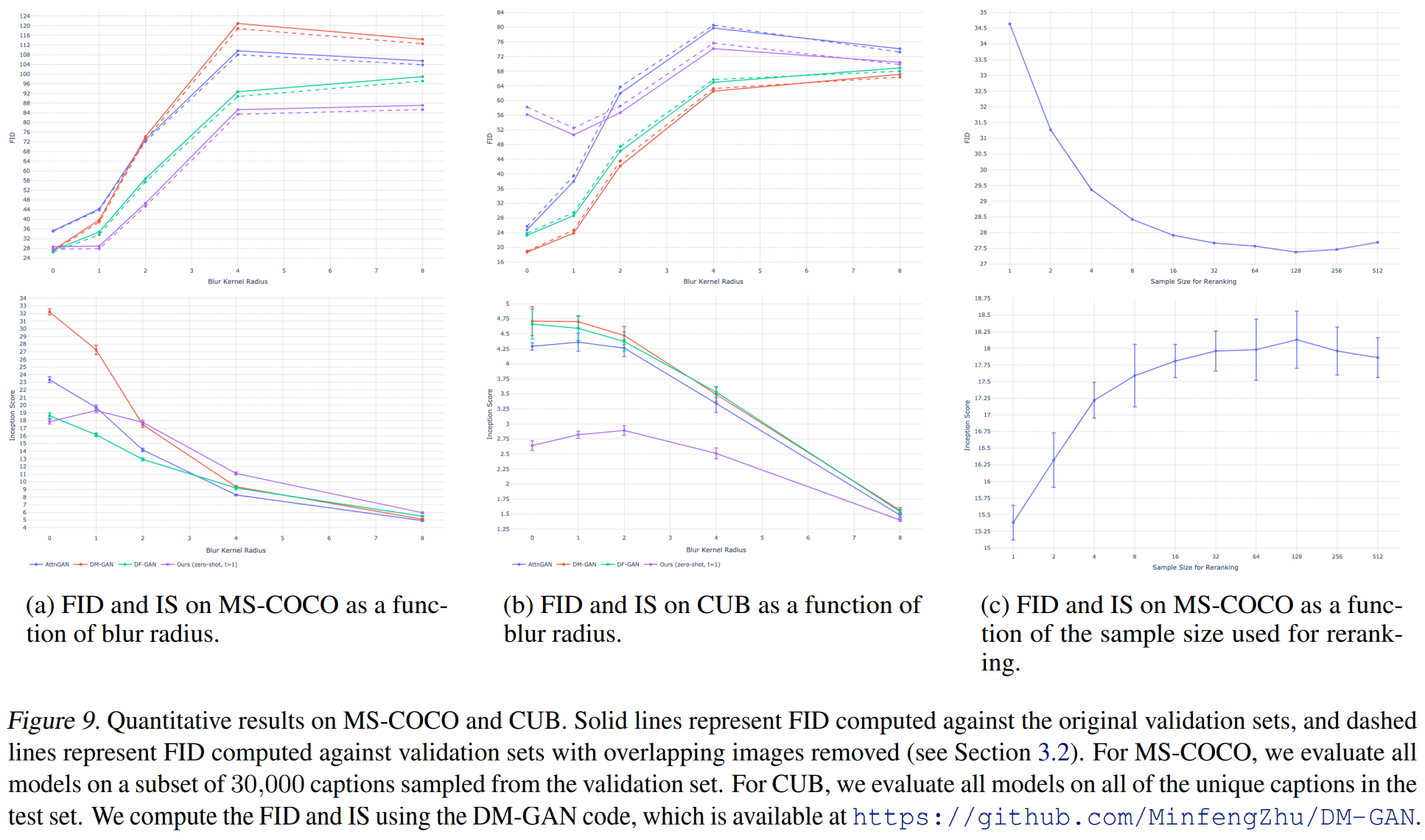
FIDについてはこちら、ISについてはこちらなどをご参照いただければと思いますが、とりあえずFIDは低いほど良い、ISは高いほど良いと思ってください。
(a)はMS-COCOデータセットで比較した場合ですが、DALL-Eは他のモデルと比べてFID(上段)は低くなっており、精度が高いことがわかります。
横軸はblur radiusとありますが、これについて説明をしておきます。
一旦VQ-VAEにより画質を落としてから、Transformerを学習し、それを復元しているというDALL-Eの仕組み上、DALL-Eの特徴として、詳細よりも全体感を捉えることができる、という特徴があります。
これにより、細かい部分を正確に生成するよりも、何の画像か?がすぐわかるようになっています。
一方で、それにより細かい部分が正確ではありません。
ということで、その効果を見ているものです。
画像をblur radiusの範囲でぼかすことによって比較しています。
blur radiusが大きくなるほど、FID、ISともに差が大きくなっていますので、DALL-Eがより全体感を捉えているということが言えるかと思います。
では、CUB(Caltech-UCSD Birds 200)データセットという200種類の鳥のみのデータセットの結果ですが、こちらについてはGANに及びません。
要因は明確ではありませんが、鳥の画像のみのデータセットということが影響しているのかもしれません。
特定のドメインで測っているので、ゼロショットのDALL-Eでは及ばないのかもしれません。
ファインチューニングをすれば良くなる可能性は十分にあります。
最後に一番右の(c)は、CLIPでランキングする数と精度を比較したものです。
ランキング数を増やすほど精度は改善しますが、32ぐらいからあまり変化しなくなっています。
Qualitative Findings
DALL-Eは、著者らがもともと想定していた以上に汎化されていたとのことです。
例えば、以下のように“アコーディオンから作られたバク。アコーディオンの模様をしたバク。”という文章を与えることで、アコーディオンとバクの概念を混ぜることができます。

他の例もありますが、ここでは画像から画像への翻訳の例を見てみましょう。
”上とまったく同じ猫のスケッチが下にある。”という文章を与えた場合です。
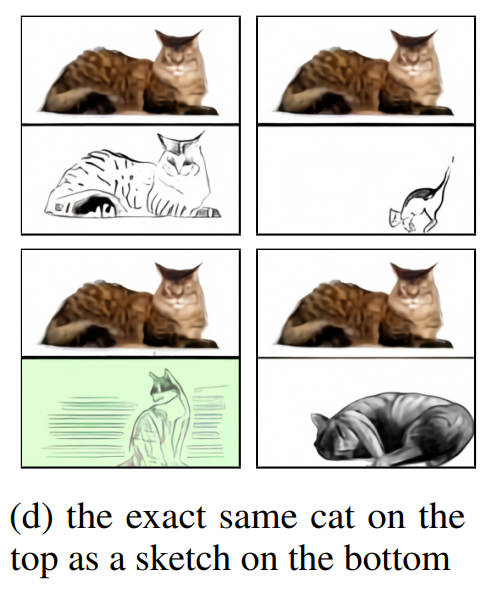
これは、猫の画像も与えていると思いますが、そのスケッチ画像を生成しています。
何かに使えそうですね。
他の例も載せておきます。
スケッチだけでなく、(b)反転させたり、(c)クローズアップしたり、(d)赤くしたり、(e)サングラスを掛けたり、(f)切手にしたり、と色んなことが可能になっています。

まとめ
以上が、DALL-Eの説明になります。
この記事では、GPUの具体的な実装方法の部分については省略しています(私があまり詳しくないので…)。
興味がある方は論文を参考にしていただければと思います。
また、DALL-Eを超えたと話題のGLIDEについても以下の記事で解説していますので、興味のある方は見てみてください。
では!







