【Python (Tensorflow) による実装付き】Variational Auto-Encoder (VAE) を理解する

今回は、2014年に提案された画像生成モデル “Variational Auto-Encoder (VAE) ” について解説していきたいと思います。

仕組みの詳細まで踏み込んでいるため、計算などが複雑にはなっていますが、極力わかりやすく説明したいと思います

VAE は日本語では"変分オート・エンコーダ"と呼ばれ、主に画像生成に用いられる技術です。

現在、VAE をそのまま利用することは少ないかもしれませんが、この技術が応用された VQ-VAE といった手法で OpenAI の『DALL-E』などが作られており、画像生成で多く利用されています。

通常のオート・エンコーダと言えば、画像などの観測値を低次元の特徴量ベクトルに圧縮することを目的としたモデルです。

例えば、顔の画像であれば、顔の向きや目の位置など、画像を決める重要な情報 (特徴量) に圧縮し、元に復元できるように圧縮方法を学習します。

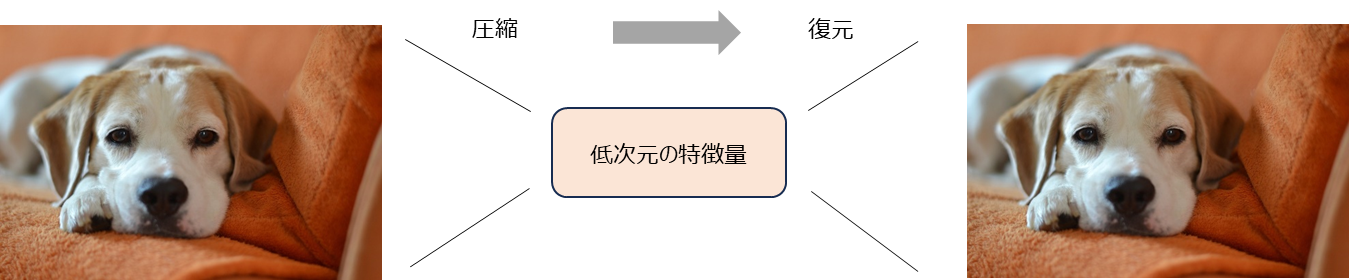
そして、画像の分類作業などを行う際に、エンコーダ部分を分類層に置き換えて、学習することにより収束しやすく精度の改善が見込まれます。

つまり分類器のための “良い初期値” として使われます。

一方で、VAE は前述の通り "画像を生成する生成モデル" です。

VAE 自体は変分推論を使った生成モデルなのですが、その結果オート・エンコーダと同じ形になっているので Variational Auto-Encoder という名前がついています。

具体的には、変分推論の考え方により以下の式を最大化しますが、2項目がデータ ${\bf{x}}$ から潜在変数 ${\bf{z}}$ に変換し(エンコーダに対応)、1項目が潜在変数 ${\bf{z}}$ からデータ ${\bf{x}}$ を復元する形(デコーダに対応)になっているので、オート・エンコーダという名前がついています。

$$\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] -D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)$$

そして、通常のオート・エンコーダでは画像を生成することはできませんが、VAE では潜在変数を事前分布からサンプリングすることにより画像の生成が可能になります。

今回は、最後に実装もつけています。

変分推論の説明も詳しくしているのでかなり長くなっていますが、最終的な仕組みは非常にシンプルなので、本記事の後半のプログラムを見ていただくと仕組みの理解は十分にできると思います。

では、とりあえず順を追って見ていきましょう。

論文はこちらです。

『Auto-Encoding Variational Bayes』

1 オート・エンコーダ(Auto-Encoder)とは
2 Variational Auto-Encoder(VAE)の概要
3 変分推論とは
4 変分推論をオート・エンコーダに適用する
5 VAEの実装
6 参考文献
7 まとめ

オート・エンコーダ(Auto-Encoder)とは

まず、オート・エンコーダについてはご存じの方も多いと思いますが、簡単に説明しておきます。

オート・エンコーダはラベルを使わない教師なし学習です。

観測データを低次元の特徴量に圧縮し、またそれを観測データに戻すという学習をします。

具体的にはエンコーダで画像などのデータ ${\bf{x}}$ を ${\bf{z}}$ に圧縮し、そこから $\hat{{\bf{x}}}$ を計算します。

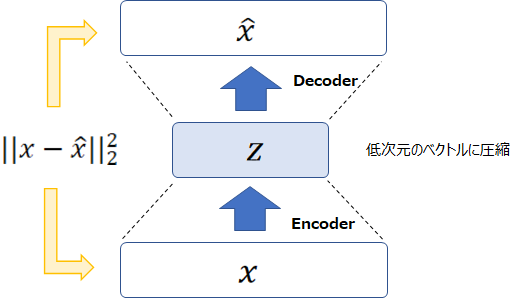
そして、二乗誤差 $\|{\bf{x}}-\hat{{\bf{x}}}\|_2^2$ を最小化するようにパラメータを学習します。

これの何が嬉しいかというと、${\bf{x}}$ の持っている重要な特徴が ${\bf{z}}$ に圧縮されることです。

それにより、個別のタスクの教師あり学習におけるパラメータの“良い初期値”として使うことができます。

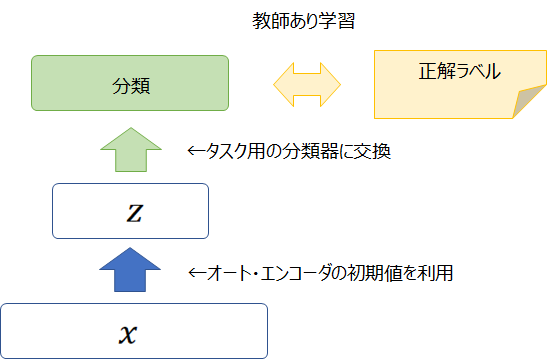
ですので、オート・エンコーダの目的は、教師あり学習の特徴量を抽出したり、良い初期値を見つけることであり、データ ${\bf{X}}$ を生成することはできません。

一方で、VAE はデータを生成することが目的です。

では、本題の VAE について見ていきます。

Variational Auto-Encoder(VAE)の概要

まず、結論を言ってしまうと VAE は以下の図のような形になります。

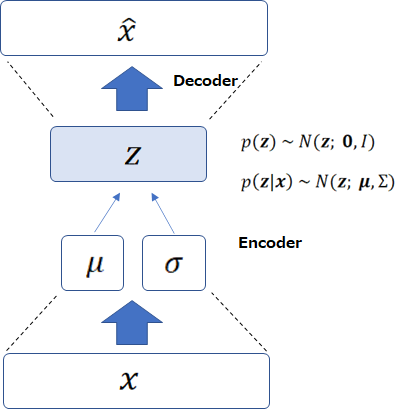
インプットを ${\bf{x}}$ として、事後分布として仮定した正規分布の平均 ${\bf{\mu}}$、分散 $\Sigma$ をニューラル・ネットワークで計算します。

次に、$N({\bf{z}}; {\bf{\mu}}, \Sigma)$ に従って潜在変数 ${\bf{z}}$ をサンプリングします。

そして ${\bf{z}}$ からニューラル・ネットワークで ${\bf{x}}$ を復号化することで学習します。

学習時の目的関数については後で説明します。

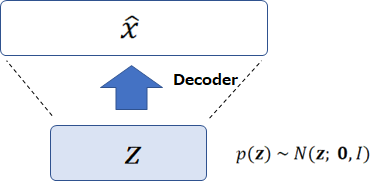
そして、VAE は上記の学習済みパラメータを使って、データ ${\bf{x}}$ を生成することが可能になります。

潜在変数 ${\bf{z}}$ の事前分布が $N({\bf{z}}; {\bf{0}}, I)$ であるという仮定をしており、その事前分布から ${\bf{z}}$ をサンプリングすることで、${\bf{x}}$ を生成することができます。

では、また学習の話に戻りましょう。

考えられる方法は、周辺対数尤度 $\log p_\theta(X)$ を最大化するという方法です ($\theta$ はニューラル・ネットワークのパラメータを表します)。

どのようにしてパラメータを学習すればよいのでしょうか？

しかしながら、対数周辺尤度は

$$\log p_\theta(X)=\sum_{n=1}^{N}\log \int_{ {\bf{z}}_n} p_\theta({\bf{x}}_n | {\bf{z}}_n) p_\theta({\bf{z}}_n)d{\bf{z}}_n$$

となりますが、この積分がやっかいです。

ニューラルネットワークを使っているので解析的には解けないのに加えて、${\bf{z}}$ の次元が高いと数値計算による積分も簡単に実行できません。

同様に事後分布

$$p_\theta({\bf{z}}_n|{\bf{x}}_n)=\frac{p_\theta({\bf{x}}_n|{\bf{z}}_n) p_\theta({\bf{z}}_n)}{p_\theta({\bf{x}}_n)}$$

についても、$p_\theta({\bf{x}}_n|{\bf{z}}_n)$ と $p_\theta({\bf{z}}_n)$ は、それぞれニューラル・ネットワークと正規分布なので問題ありませんが、分母にまた $p_\theta({\bf{x}}_n)$ が出てきており、これが計算できません。

そこで出てくるのが変分推論 (Variational Inference) です。

結論を言うと、以下を最大化します。

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta)&=\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] -D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

ここから詳細に入っていきますので、詳細よりも仕組みを理解したい方は実装まで飛んでいただければと思います。

変分推論とは

上で事後分布 $p_{\theta}({\bf{z}}|{\bf{x}})$ は計算することができないと言いましたが、変分推論はその解析的には解けない事後分布 $p_{\theta}({\bf{z}}|{\bf{x}})$ を近似的に求める手法です。

変分推論では、事後分布 $p_{\theta}({\bf{z}}|{\bf{x}})$ の近似分布として $q_\phi({\bf{z}}|{\bf{x}})$ を導入します。

$\phi$ は変分パラメータ (variational parameter) と呼ばれます。

この $q_\phi({\bf{z}}|{\bf{x}})$ を使って周辺対数尤度 $\log p_\theta({\bf{x}})$ を少し変形していきます。

そして、周辺対数尤度 $\log p_\theta(X)$ の最大化ではなく、周辺対数尤度の下界の最大化という問題に置き換えます。

では、詳細を見ていきましょう。

下界の導出

わかりやすくするため1つのサンプルで計算していきます。

まず、周辺対数尤度を

$$\begin{align}
\log p_\theta({\bf{x}})&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log p_\theta({\bf{x}}) d{\bf{z}}
\end{align}$$

と書きます。( $p_\theta({\bf{x}})$は${\bf{z}}$ に依存しないから)

そして、

$$\begin{align}
\log p_\theta({\bf{x}})&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log \frac{p_\theta({\bf{x}}, {\bf{z}})}{p_\theta({\bf{z}}|{\bf{x}})} d{\bf{z}}\\
&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log \frac{p_\theta({\bf{x}}, {\bf{z}})}{p_\theta({\bf{z}}|{\bf{x}})}\frac{q_\phi({\bf{z}}|{\bf{x}})}{q_\phi({\bf{z}}|{\bf{x}})} d{\bf{z}}\\
&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log \frac{p_\theta({\bf{x}}, {\bf{z}})}{q_\phi({\bf{z}}|{\bf{x}})} d{\bf{z}} - \int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log \frac{p_\theta({\bf{z}}|{\bf{x}})}{q_\phi({\bf{z}}|{\bf{x}})} d{\bf{z}}\\
\end{align}$$

と変形することができます。

1行目はベイズの定理を使っています。

2行目は分母分子に $q_\phi({\bf{z}}|{\bf{x}})$ を掛けただけです。

この1項目は${\bf{x}}$、$\phi$、$\theta$ の関数になっているので $\mathcal{L}({\bf{x}}, \phi, \theta)$ として定義します。

$$\mathcal{L}({\bf{x}}, \phi, \theta)=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log \frac{p_\theta({\bf{x}}, {\bf{z}})}{q_\phi({\bf{z}}|{\bf{x}})} d{\bf{z}}$$

そして、2項目は分布 $q_\phi({\bf{z}}|{\bf{x}})$ と $p_\theta({\bf{z}}|{\bf{x}})$ の KL ダイバージェンス(分布間の距離のようなもの)の形になっていますので、

$$D_{KL}\left(q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}|{\bf{x}})\right)=- \int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}}) \log \frac{p_\theta({\bf{z}}|{\bf{x}})}{q_\phi({\bf{z}}|{\bf{x}})} d{\bf{z}}$$

とします。

すると、周辺対数尤度は、

$$\begin{align}
\log p_\theta({\bf{x}})&=\mathcal{L}({\bf{x}}, \phi, \theta)+D_{KL}(q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}|{\bf{x}}))
\end{align}$$

と書くことができます。

さて、こう書き換えたところで、周辺対数尤度が計算できるようになったわけではありません。

なぜなら、KL ダイバージェンスの項に計算できない $p_\theta({\bf{z}}|{\bf{x}})$ があるからです。

しかしながら、よく考えると KL ダイバージェンスは0以上の値しか取らず、左辺は $q_\phi({\bf{z}}|{\bf{x}})$ の影響を受けません。

したがって、近似分布のパラメータ $\phi$ を動かすことを考えた場合、

$$\log p_\theta({\bf{x}})\ge\mathcal{L}({\bf{x}}, \phi, \theta)$$

となることがわかります。

つまり、$\mathcal{L}({\bf{x}}, \phi, \theta)$ は周辺対数尤度の下界となっているということです(平たく言うと下限になっているということですね)。

この下界は ELBO(Evidence Lower Bound) や VLB(Variational Lower Bound) と呼ばれます。

そして、この下界 $\mathcal{L}({\bf{x}}, \phi, \theta)$ を最大化することで、周辺対数尤度を最大化しよう、というものです。

下界が最大になるのは、$D_{KL}(q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}|{\bf{x}}))$ がゼロになるときですので、分布 $q_\phi({\bf{z}}|{\bf{x}})$ を $p_\theta({\bf{z}}|{\bf{x}})$ に限りなく近づけることで下界が最大になります。

下界の計算

では、下界を実際に計算するため、もう少し変形すると、

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta)&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log \frac{p_\theta({\bf{x}}, {\bf{z}})}{q_\phi({\bf{z}}|{\bf{x}})}d{\bf{z}}\\
&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log \frac{p_\theta({\bf{x}}|{\bf{z}})p_\theta({\bf{z}})}{q_\phi({\bf{z}}|{\bf{x}})}d{\bf{z}}\\
&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log p_\theta({\bf{x}}|{\bf{z}})d{\bf{z}} + \int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log \frac{p_\theta({\bf{z}})}{q_\phi({\bf{z}}|{\bf{x}})}d{\bf{z}}\\
&= \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] -D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

となります。

ここで、1項目の期待値計算が問題になってきます。

期待値自体は、モンテカルロ法を使って、$q_\phi({\bf{z}}|{\bf{x}})$ に従う乱数${\bf{z}}$を振ることによって、

$$\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right]\simeq \frac{1}{L}\sum_{l=1}^L \log p_\theta({\bf{x}}|{\bf{z}}^{(l)}), \hspace{10pt}{\bf{z}}^{(l)}～q_\phi({\bf{z}}|{\bf{x}})$$

として計算することが可能です。

ですので、下界 $\mathcal{L}({\bf{x}}, \phi, \theta)$ を求めることは可能です。

しかしながら、パラメータ $\phi$ の推定のために勾配を計算しようとすると、$q_\phi({\bf{z}}|{\bf{x}})$ に従う乱数 ${\bf{z}}^{(l)}$ を振ってしまったあとでは、$\phi$ について微分が計算できません。

一つのやり方としては、スコア関数推定 (Score Function Estimator) という手法がありますが、こちらは分散が高く勾配の推定値としてはあまり良くありません。

制御変量法などを使うことによりより良い勾配を得ることが可能ですが、ここでは reparameterization trick(再パラメータ化) という非常にシンプルで効率的な手法を使って勾配を推定できるようにします。

論文では一般論についても解説されていますが、VAEの例を挙げた方がわかりやすいと思いますので、次の節で具体例とともに見ていきたいと思います。

変分推論をオート・エンコーダに適用する

では、変分推論の説明が終わったところで、VAEに入りたいと思います。

VAE では、事後分布 $p_\theta({\bf{z}}|{\bf{x}})$ は正規分布に従うとします。

そして、潜在変数 ${\bf{z}}$ を直接ニューラル・ネットワークで求めるのではなく、$p_\theta({\bf{z}}|{\bf{x}})$ の平均と分散をニューラル・ネットワークにより求めます。

つまり、

$$q_\phi({\bf{z}}|{\bf{x}})=N\left({\bf{z}}; \mu(\phi), \Sigma(\phi)\right)$$

という形です。

ただし、$\Sigma$ は対角行列とし、共分散項はゼロで ${\bf{z}}$ の要素は互いに独立になります。

図で描くとこのようになります。

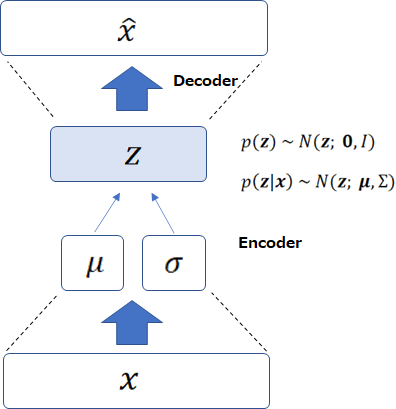
そして、パラメータ $\theta$ と $\phi$ を同時に求めます。

ところで、上の図を見るとエンコーダ・デコーダの形になっています。

$q_\phi({\bf{z}}|{\bf{x}})$ が ${\bf{x}}$ から潜在変数${\bf{z}}$を求めるエンコーダで、$p_\theta({\bf{x}}|{\bf{z}})$ が潜在変数 ${\bf{z}}$ から ${\bf{x}}$ を求めるデコーダです。

これが、Variational Auto-Encoder と呼ばれる所以です。

ちなみに、エンコーダは認識ネットワーク (recognition network) または推論ネットワーク(inference network) と呼ばれます。

デコーダは生成ネットワーク (generative network) と呼ばれます。

そして、データを生成する際は、事前分布 $p_\theta({\bf{z}})～N({\bf{z}}; {\bf{0}}, I)$ から ${\bf{z}}$ をサンプリングすることにより生成します。

これは ${\bf{z}}$ の事前分布を仮定していることから、サンプリングが可能になっています。

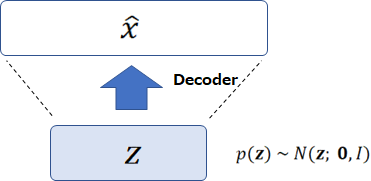
では、また学習の話に戻って、下界 $\mathcal{L}({\bf{x}}, \phi, \theta)$ を最大化しましょう。

下界 $\mathcal{L}({\bf{x}}, \phi, \theta)$ は次のように表されました。

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta)&= \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] - D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

そして、$\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right]$ の勾配 $\nabla \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right]$ を計算する必要があります。

ここで、Reparameterization Trick (再パラメータ化) という手法を導入します。

Reparameterization Trick(再パラメータ化)

モンテカルロ法によって $\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right]$ の勾配を計算する場合、$q_\phi({\bf{z}}|{\bf{x}})～N({\bf{z}}; \mu(\phi), \Sigma(\phi))$ に従う乱数を振ってしまうと、あとからパラメータ $\phi$ によって微分しようとしても微分できないという問題がありました。

そこで Reparameterization Trick の出番なのですが、${\bf{z}}^{(l)}$ は平均 $\mu$、共分散行列 $\Sigma$ (対角行列)の正規分布に従うと仮定しているので、

$${\bf{z}}^{(l)} = \mu(\phi) + \sigma(\phi) \odot {\bf{\epsilon}}^{(l)}, \hspace{10pt} {\bf{\epsilon}}^{(l)}～N({\bf{\epsilon}}^{(l)}; {\bf{0}}, I)$$

と書くことができます。

$\sigma(\phi)$ は $\Sigma$ の対角成分の平方根を表します(ようは各成分の標準偏差)。

これにより、変分パラメータ $\phi$ で微分することが可能になります。

したがって、

$$\begin{align}
\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right]&\simeq \frac{1}{L} \sum_{l=1}^L \log p_\theta({\bf{x}}|{\bf{z}}^{(l)}), \\
{\bf{z}}^{(l)}&=\mu(\phi) + \sigma(\phi) \odot {\bf{\epsilon^{(l)}}}, \hspace{10pt} \epsilon^{(l)}～N(\epsilon; 0, I)
\end{align}$$

となります。

例えば、$\phi$ で微分すると、

$$\frac{\partial z^{(l)}}{\partial \phi} = \frac{\partial \mu(\phi)}{\partial \phi} + \frac{\partial \sigma(\phi)}{\partial \phi} \epsilon^{(l)}$$

という形で勾配を計算することが可能です。

一般的に $L=1$ として計算されることが多いようです。

この項を再構築誤差 (reconstruction error) 項と呼びます。

KLダイバージェンス項

あとは、KL ダイバージェンスの項

$$\begin{align}
-D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log \frac{p_\theta({\bf{z}})}{q_\phi({\bf{z}}|{\bf{x}})}d{\bf{z}}\\
&=\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log p_\theta({\bf{z}})d{\bf{z}} - \int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log q_\phi({\bf{z}}|{\bf{x}})d{\bf{z}}
\end{align}$$

です。

$q_\phi({\bf{z}}|{\bf{x}})$は$N({\bf{z}}; \mu, \Sigma)$ に従い ($\Sigma$は対角行列)、$p_\theta({\bf{z}})$は$N(z; {\bf{0}}, I)$ に従うと仮定しているので、解析的に計算することが可能です。

それではまず1項目を計算していきましょう。

ちなみに、ただひたすら計算するだけなので飛ばしていただいても大丈夫です(他にもっと簡単に計算する方法がありそうですし)。

ただ、一度自分で解いておくと、よりしっくりくるのかなと思います。

$D$ は ${\bf{z}}$ の次元、$\sigma_j$ は $\Sigma$ の $j$ 番目の対角成分を表します。

$$\begin{align}
\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log p_\theta({\bf{z}})d{\bf{z}}&=\int_{\bf{z}} N({\bf{z}}; \mu, \Sigma) \log N({\bf{z}}; {\bf{0}}, I)d{\bf{z}} \\
&=\int_{\bf{z}} N({\bf{z}}; \mu, \Sigma)
\left( \log \frac{1}{\sqrt{(2\pi)^D }} -\frac{{\bf{z}}^T{\bf{z}}}{2}\right) d{\bf{z}} \\
&=\log \frac{1}{\sqrt{(2\pi)^D }} -\int_{\bf{z}} N({\bf{z}}; \mu, \Sigma)\frac{{\bf{z}}^T{\bf{z}}}{2}d{\bf{z}}\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\mathbb{E}_{N({\bf{z}}; \mu, \Sigma)}\left[{\bf{z}}^T{\bf{z}}\right]\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\mathbb{E}_{N(z_j; \mu_j, \sigma_j^2)}\left[\sum^D_{j=1}z_j^2\right]\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\sum^D_{j=1}\left(\mu_j^2+\sigma_j^2\right)
\end{align}$$

4行目から5行目は、${\bf{z}}$ の共分散がゼロであることを利用しています。

次に2項目です。

$\Sigma$ は対角行列なので、行列式は $|\Sigma|=\prod_{j=1}^{D}\sigma_j$ となります。

$$\begin{align}
\int_{\bf{z}} q_\phi({\bf{z}}|{\bf{x}})\log q_\phi({\bf{z}})d{\bf{z}}&=\int_{\bf{z}} N({\bf{z}}; \mu, \Sigma) \log N({\bf{z}}; \mu, \Sigma)d{\bf{z}} \\
&=\int_{\bf{z}} N({\bf{z}}; \mu, \Sigma)
\left( \log \frac{1}{\sqrt{(2\pi)^D |\Sigma|}} -\frac{1}{2}({\bf{z}}-\mu)^T\Sigma^{-1}({\bf{z}}-\mu)\right)d{\bf{z}} \\
&=\log \frac{1}{\sqrt{(2\pi)^D |\Sigma|}} - \frac{1}{2}\int_{\bf{z}} N({\bf{z}}; \mu, \Sigma)({\bf{z}}-\mu)^T \Sigma^{-1} ({\bf{z}}-\mu)d{\bf{z}}\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\log |\Sigma| -\frac{1}{2}\mathbb{E}_{N({\bf{z}}; \mu, \Sigma)}\left[({\bf{z}}-\mu)^T\Sigma^{-1} ({\bf{z}}-\mu)\right]\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\log\prod_{j=1}^D \sigma_j^2-\frac{1}{2}\mathbb{E}_{N(z_j; \mu_j, \sigma_j^2)}\left[\sum^D_{j=1}\left(\frac{z_j-\mu}{\sigma_j}\right)^2\right]\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\sum_{j=1}^D\log \sigma_j^2-\frac{1}{2}\sum_{j=1}^D1\\
&=-\frac{D}{2}\log(2\pi)-\frac{1}{2}\sum^D_{j=1}\left(1+\log \sigma_j^2\right)
\end{align}$$

ですので、最終的に

$$D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)=-\frac{1}{2}\sum_{j=1}^{D}\left(1+\log \sigma^2_j - \mu_j^2 -\sigma^2\right)$$

と解析的に計算できるようになります。

下界計算式のまとめ

では、最終的な下界の計算式は以下のようになります。

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta) &= \frac{1}{L} \sum_{l=1}^L \log p_\theta({\bf{x}}|{\bf{z}}^{(l)}) + \frac{1}{2}\sum_{j=1}^{D}\left(1+\log \sigma^2_j - \mu_j^2 -\sigma_j^2\right)\\
{\bf{z}}^{(l)}&=\mu(\phi) + \sigma(\phi) \odot \epsilon^{(l)}, \hspace{10pt} \epsilon^{(l)}～N(\epsilon; {\bf{0}}, I)
\end{align}$$

1項目が再構築項で、2項目が KL ダイバージェンス項です。

KL ダイバージェンス項は正則化項としてみなせます。

VAEの実装

ここでは、Tensorflow を使って VAE を実装したいと思います。

PyTorch を使った実装はこちらをご参照ください。

: 【PyTorch】VAE(Variational Auto-Encoder)を実装する
さて、以前こちらの記事ではVAE(Variational Auto-Encoder)の解説およびTensorflowを使った実装をしました。 https://data-analytics.fun/20 ...

まず、必要なライブラリをインポートします。

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow import keras
from keras.datasets import mnist
from keras import backend as K
from tensorflow.keras.layers import Input, Dense, Lambda
%matplotlib inline

MNIST データセットをロードして整形します。

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

エンコーダの実装です。

class Encoder(tf.keras.Model):
  def __init__(self, input_dim, hidden_dim, latent_dim):
    super(Encoder, self).__init__()
    self.input_dim = input_dim
    self.hidden_dim = hidden_dim
    self.latent_dim = latent_dim
    self.dense_1 = Dense(self.hidden_dim, activation='relu')
    self.dense_mu = Dense(self.latent_dim, activation='linear')
    self.dense_sigma = Dense(self.latent_dim, activation='linear')

  def call(self, x_input):
      hidden = self.dense_1(x_input)
      mu = self.dense_mu(hidden)
      log_sigma = self.dense_sigma(hidden)
      eps = K.random_normal(shape=(self.latent_dim,), mean=0., stddev=0.1)
      z = mu + K.exp(log_sigma) * eps
      
      return mu, log_sigma, z

インプット ${\bf{x}}$ から、最初の層で隠れ層のベクトルを計算し、そこからニューラル・ネットワークを使って潜在変数を ${\bf{z}}$ の平均 $\mu$、標準偏差 $\sigma$ の対数をそれぞれ計算します。

$\sigma$ の対数を取っているのは、単純に負の値を許容するためです。

そして、15行目で、正規乱数 $\epsilon$ をサンプリングし、reparameterization trick を使って潜在変数 ${\bf{z}}$ をサンプリングします。

続いて、デコーダです。

デコーダは潜在変数 ${\bf{z}}$ から ${\bf{x}}$ を再構築します。

class Decoder(tf.keras.Model):
  def __init__(self, input_dim, hidden_dim, latent_dim):
    super(Decoder, self).__init__()
    self.input_dim = input_dim
    self.hidden_dim = hidden_dim
    self.latent_dim = latent_dim
    self.dense_1 = Dense(self.hidden_dim, activation='relu')
    self.dense_output = Dense(self.input_dim, activation='sigmoid')

  def call(self, z):
      hidden = self.dense_1(z)
      output = self.dense_output(hidden)
      return output

そして、エンコーダとデコーダを合わせたものが、VAEの全体になります。

class VAE(tf.keras.Model):
  def __init__(self, input_dim, hidden_dim, latent_dim):
    super(VAE, self).__init__()
    self.encoder = Encoder(input_dim, hidden_dim, latent_dim)
    self.decoder = Decoder(input_dim, hidden_dim, latent_dim)
  
  def call(self, x):
    mu, log_sigma, z = self.encode(x)
    x_decoded = self.decoder(z)
    return mu, log_sigma, x_decoded, z

  def encode(self, x):
    mu, log_sigma, z = self.encoder(x)
    return mu, log_sigma, z

  def decode(self, z):
    x_decoded = self.decoder(z)
    return x_decoded

続いて、損失関数です。

目的関数は下界の最大化なので、損失関数としては負の下界になり、以下で表されます。

$$\begin{align}
\text{Loss Function} &= -\frac{1}{L} \sum_{l=1}^L \log p_\theta({\bf{x}}|{\bf{z}}^{(l)}) + \frac{1}{2}\sum_{j=1}^{D}\left(1+\log \sigma^2_j - \mu_j^2 -\sigma_j^2\right)\\
{\bf{z}}^{(l)}&=\mu(\phi) + \sigma(\phi) \odot \epsilon^{(l)}, \hspace{10pt} \epsilon^{(l)}～N(\epsilon; {\bf{0}}, I)
\end{align}$$

1項目は負の対数尤度なのでクロス・エントロピー誤差として計算できます。

そして、KL ダイバージェンス項については、前節で導出した

$$D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)=-\frac{1}{2}\sum_{j=1}^{D}\left(1+\log \sigma^2_j - \mu_j^2 -\sigma_j^2\right)$$

を使います。

この2つの合計が損失関数の値になります。

def loss_function(label, predict, mu, log_sigma):
  reconstruction_loss = tf.keras.losses.binary_crossentropy(label, predict)
  reconstruction_loss *= 768
  kl_loss = 1 + log_sigma - K.square(mu) - K.exp(log_sigma)
  kl_loss = K.sum(kl_loss, axis=-1)
  kl_loss *= -0.5
  vae_loss = K.mean(reconstruction_loss + kl_loss)
  return vae_loss

学習用の関数を用意します。

@tf.function
def train_step(x):
    loss = 0
    with tf.GradientTape() as tape:
        mu, log_sigma, x_reconstructed, z = vae(x, training=True)
        loss += loss_function(x, x_reconstructed, mu, log_sigma)
    batch_loss = (loss / len(x))
    variables = vae.trainable_variables
    gradients = tape.gradient(loss, variables)
    optimizer.apply_gradients(zip(gradients, variables))
    
    # accuracyの計算用
    return batch_loss

オプティマイザはAdamを使いましょう (必ずというわけではありません)。

optimizer = tf.keras.optimizers.Adam(beta_1=0.9, beta_2=0.98, 
                                     epsilon=1e-9)

学習用のデータセットを作成します。

BUFFER_SIZE = 256
BATCH_SIZE = 256
dataset = tf.data.Dataset.from_tensor_slices((x_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
steps_per_epoch = len(x_train) // BATCH_SIZE # 何個に分けるか

これで準備ができたので、学習してみましょう。

EPOCHS = 300
vae = VAE(input_dim=x_train.shape[-1], hidden_dim=64, latent_dim=2)
for epoch in range(EPOCHS):
  for batch, x in enumerate(dataset):
    batch_loss = train_step(x)
    #if batch % 100 == 0:
  print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
                                                     batch,
                                                     batch_loss.numpy()))

では、結果を見ていきます。

上の学習用コードの3行目に以下のようなコードを入れれば、適宜 ${\bf{z}}$ の分布を出力してくれます。

if epoch % 20 == 0:
　mu, sigma, z = vae.encode(x_test) # 0番目：平均, 1番目: log標準偏差, 2番目: 潜在変数
  z = z.numpy()
  plt.figure(figsize=(6, 6))
  for i in range(10):
    index = y_test == i
    plt.scatter(z[index, 0], z[index, 1], label=str(i), alpha=0.4)
    z1_mean = z[index, 0].mean()
    z2_mean = z[index, 1].mean()
    plt.annotate(str(i), (z1_mean, z2_mean))

  plt.legend()
  plt.show()

以下は初期値による潜在変数の分布ですが、まったくランダムな状態です。

つまり、潜在変数 $z$ は何の特徴もとらえていません。

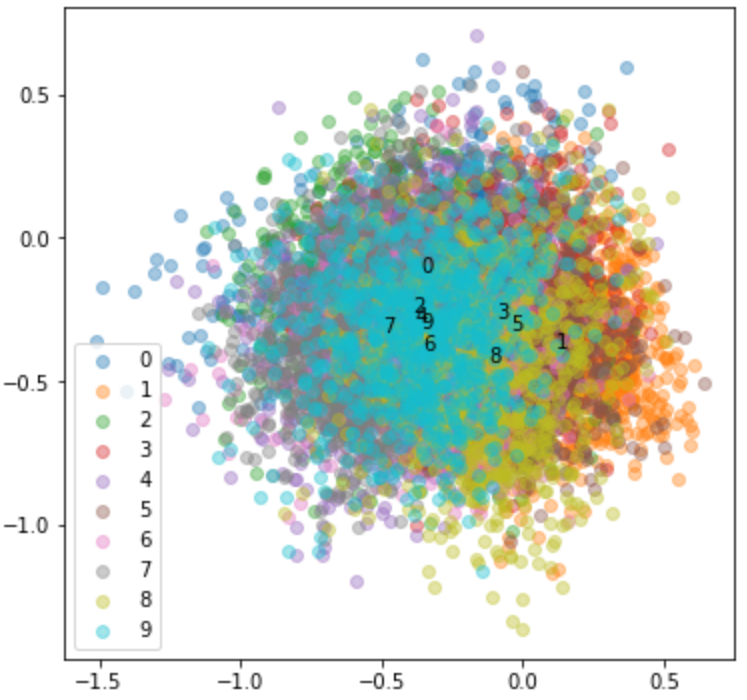
続いて20エポック学習後です。

特徴を捉えて分離されてきましたね。

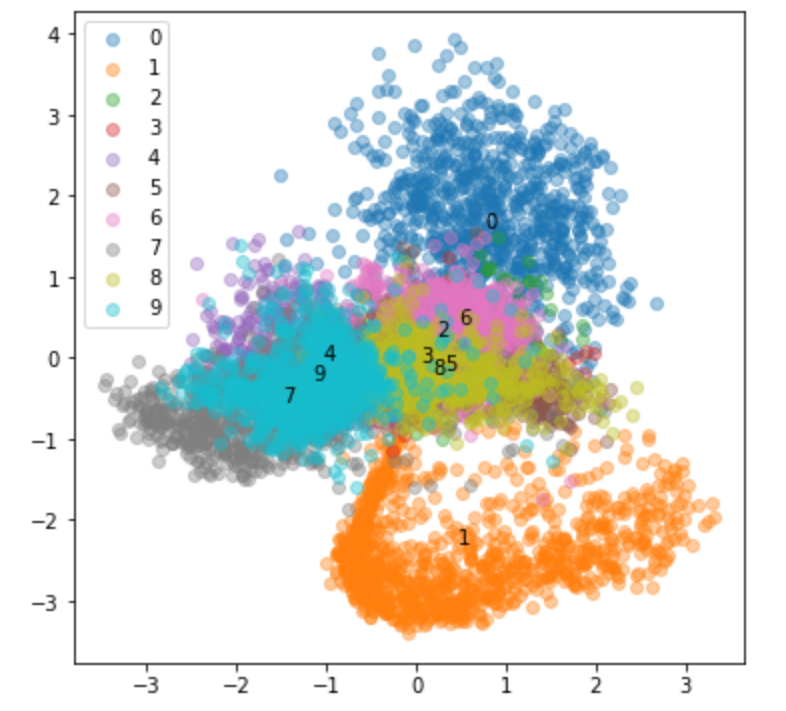
続いて、300エポック学習後です。

かなり分離されており、4と9、3と8が近く、0と6などが近くなっています。

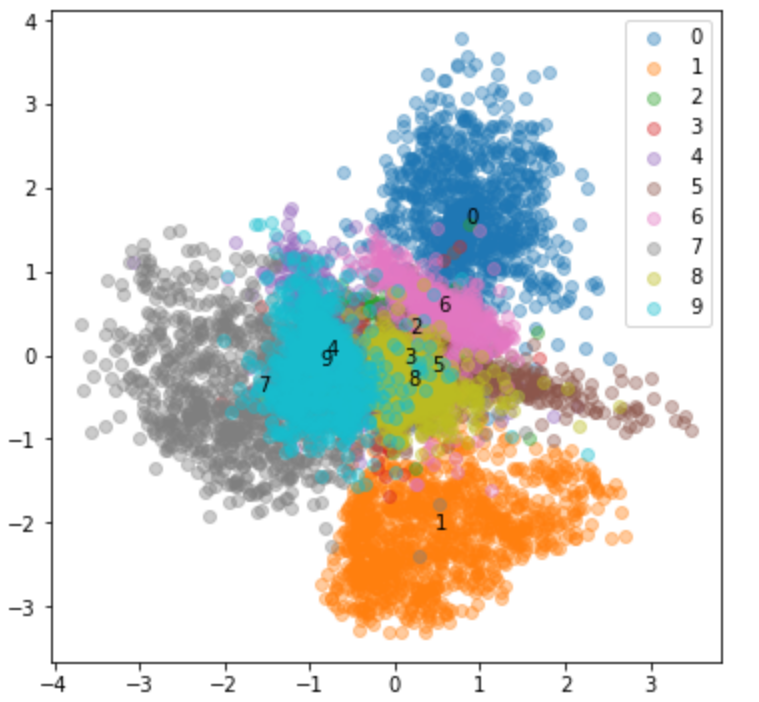
では、インプットの画像とVAEにより再構築した画像を確認してみましょう。

i = 5
mu, log_sigma, reconstructed, z = vae(x_train[i].reshape(1, -1))# * 255
print('ラベル: ', y_train[i])
fig, ax = plt.subplots(nrows=1, ncols=2)
ax[0].imshow(x_train[i].reshape(28, 28) * 255, cmap='Greys');
ax[0].set_title('original')
ax[1].imshow(reconstructed.numpy().reshape(28, 28) * 255, cmap='Greys');
ax[1].set_title('reconstructed')
plt.show()

潜在変数 $z$ を2次元にしているので、かなり粗くなっています。

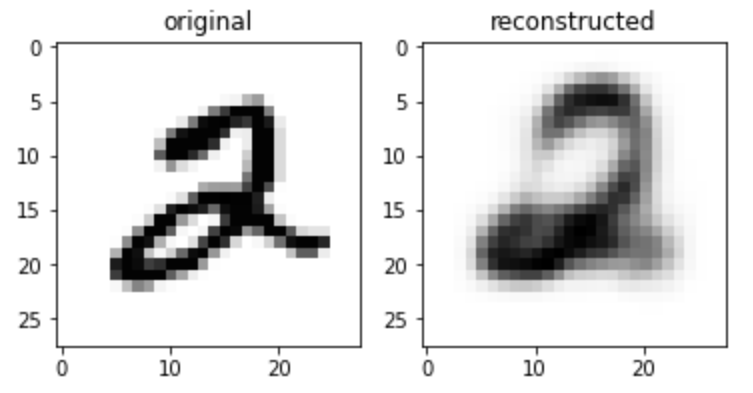
潜在変数の次元を64次元にした場合、少しクリアになっています。

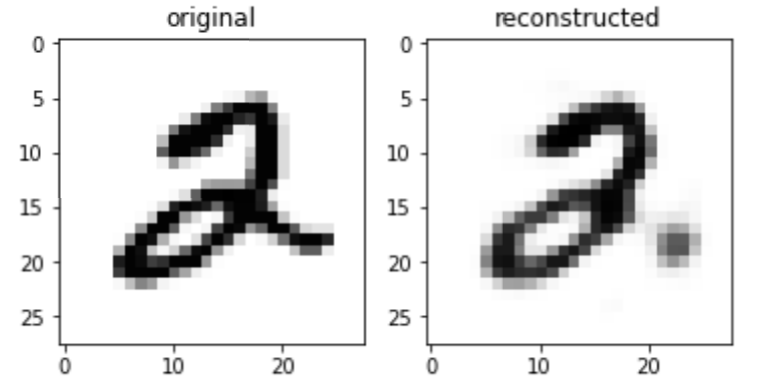
では、$z$ を矢印のように(2, 1)から(-2, 1)に動かすとどうなるでしょうか？

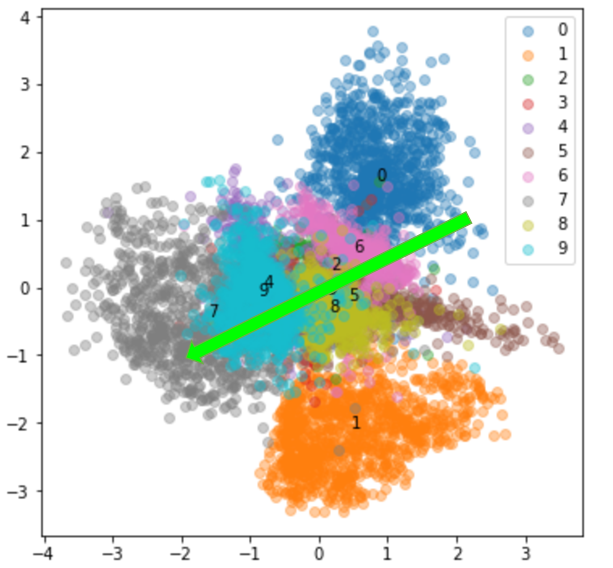
こちらを実行してみましょう。

z1 = np.linspace(-2, 2, 100)
z2 = np.linspace(-1, 1, 100)

num_of_rows = 10
fig, ax = plt.subplots(nrows=num_of_rows, ncols=num_of_rows, figsize=(10, 10))
for i, (z1_, z2_) in enumerate(zip(z1, z2)):
  sampled = vae.decode(np.array([z1_, z2_]).reshape(1, 2))
  ax[divmod(i, num_of_rows)].imshow(sampled.numpy().reshape(28, 28) * 255, cmap='Greys');
  ax[divmod(i, num_of_rows)].set_axis_off()
plt.show()

すると、このようになります。

0から6、2、3、8、9、7と連続的に変わっていくのがわかりますね(左上からスタートして、右に進み、一番右まできたら一つ下の段の一番左に続きます)。

最後に、目的である画像の生成をしてみましょう。

事前分布 $p({\bf{z}})～N({\bf{z}}: {\bf{0}}, I)$ からサンプリングして数字を生成します。

num_of_rows = 10
fig, ax = plt.subplots(nrows=num_of_rows, ncols=num_of_rows, figsize=(10, 10))
for i in range(100):
  sampled = vae.decode(np.random.normal(0, 1, size=2).reshape(1, 2))
  ax[divmod(i, num_of_rows)].imshow(sampled.numpy().reshape(28, 28) * 255, cmap='Greys');
  ax[divmod(i, num_of_rows)].set_axis_off()
plt.show()