以前、以下の記事ではVQ-VAE(Vector-Quantized Variational Auto-Encoder)をTensorflowで実装しました。
今回は、TensorflowではなくPyTorchを使っている人も多いと思いますので、PyTorchでVQ-VAEを実装したいと思います。
細かいモデルの説明は省略しますので、必要に応じて上記の記事をご参照ください。
なお、VQ-VAEで画像を生成するは、インプット画像を潜在変数に符号化して元の画像を復元するオートエンコーダ部分と、潜在変数の分布を学習して潜在変数を生成する部分にわかれますが、今回はオートエンコーダ部分だけを実装していきます。
潜在変数を生成する部分はまた何かのモデル(論文ではPixelCNN)で実装したいと思います。
VQ-VAEの概要
まず、VQ-VAEについてざっくり解説します。
VQ-VAEは潜在変数を使った画像の生成モデルで、VAE(Variational Auto-Encoder)と似たような考え方です。
以下の図だと、犬の画像をエンコーダで潜在変数にマッピングし、デコーダで犬の画像を復元するように学習します。
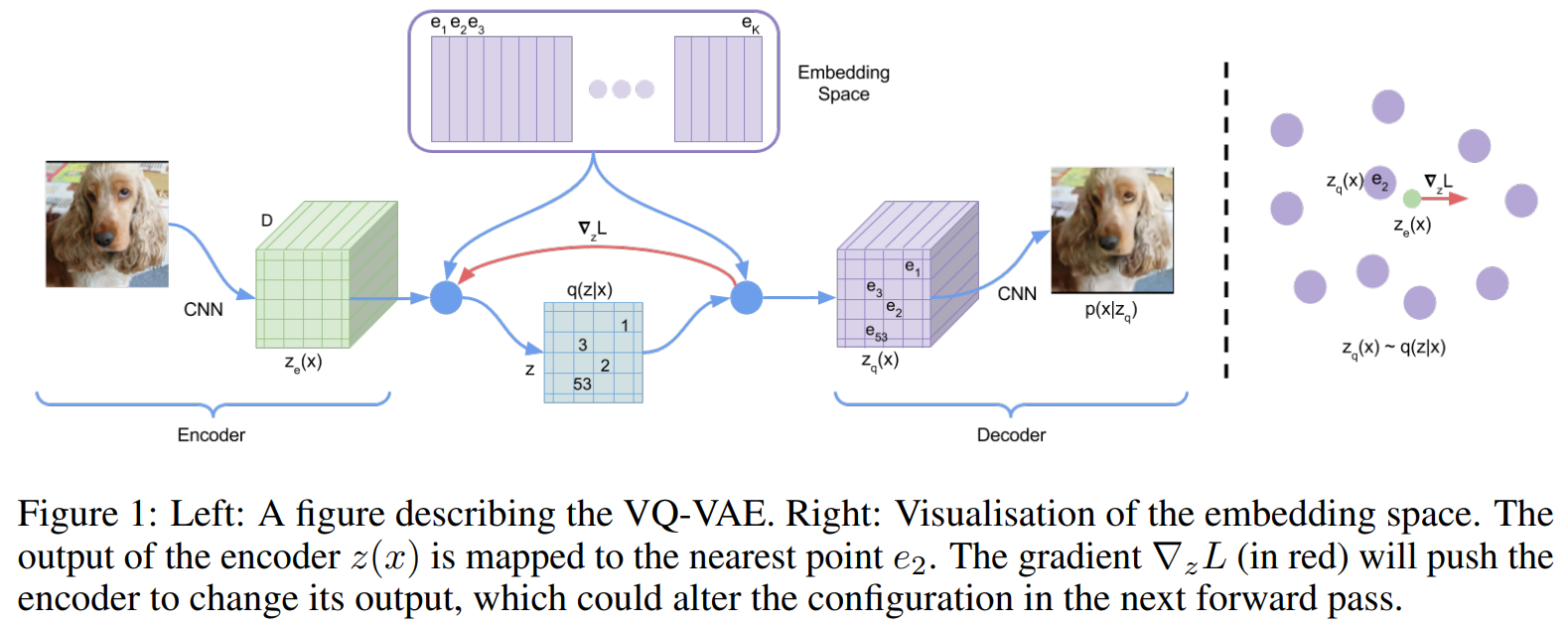
ではVQ-VAEの特徴はというと、潜在変数が離散的なベクトルで表されるという点です。
先に実装イメージを記載しておくと、以下のような処理になります(詳細は少しずつ説明します)。
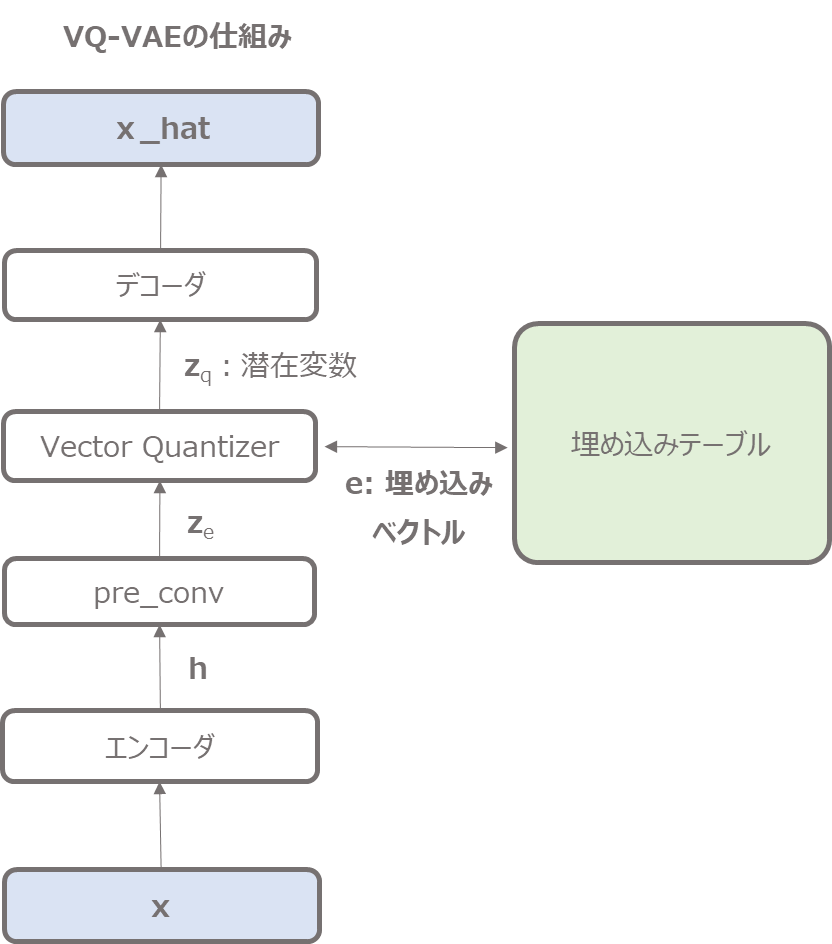
離散的なベクトルで表現とは
具体的には、エンコーダで\(z_e\)という潜在変数の一歩手前みたいなものを求めますが、そこから離散的なK種類の埋め込み表現(Embeddings)にマッピングします。
以下がマッピングされた潜在変数ですが、各セルが\({\bf{e}}_1, {\bf{e}}_2, ...\)となっています。
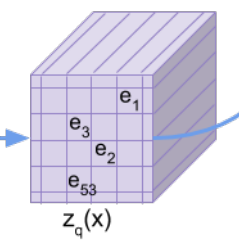
この\({\bf{e}}_1, {\bf{e}}_2, ...\)は、こちらのEmbedding Spaceと呼ばれる埋め込み表現の空間から一つ選んだものになっています。
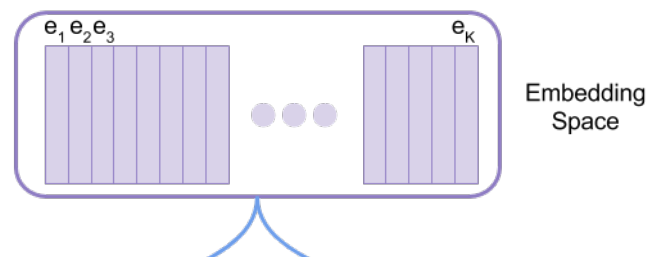
つまり、自由に値を取れるベクトルを埋め込み表現とするのではなく、各セルの値を\(K\)種類のベクトル(辞書みたいなもの)から一つ選んで設定する、というのがVQ-VAEの特徴です。
埋め込みベクトルの選び方
エンコーダで計算した\(z_e\)ともっとも距離が近い埋め込み表現\(e_j\)を選びます。
数式で書くと以下のようになります。
$$z_q(x)=e_k, \hspace{10pt}\text{where } k=\arg\min_j\|z_e(x)-e_j\|_2$$
ここで、argminを取ると、その勾配が計算できないという問題が発生しますが、ここでは勾配を計算せず、その前のレイヤーから流れてきた勾配をそのまま流すというstraight estimatorという手法を使っています。
損失関数
損失関数は以下になります。
$$L=\log p\left(x|z_q(x)\right) + \left\|\text{sg}[z_e(x)]-e \right \|^2_2 + \beta \left\|z_e(x)-\text{sg}[e]\right\|^2_2$$
1項目は再構築誤差項になります(実装では二乗誤差を使っています)。
2項目は埋め込み表現を更新するための誤差項になります。
sgというのはStop Gradientの略で、勾配を計算しないということです。
3項目は、エンコーダーのアウトプット\(z_e\)が埋め込み表現\(e\)に対して、先にどんどん更新されないようにする項になります。
各項のより詳しい説明は『【論文解説+Tensorflowで実装】VQ-VAEを理解する』をご参照いただければと思います。
画像の生成について
以上はオートエンコーダ部分の仕組みでした。
これにより、画像が与えられたら、低次元の潜在変数にマッピングして、再度もとの画像を復元することができます。
しかし、実際に新しい画像を生成するには、潜在変数を何等かのやり方で生成しなければなりません。
VAEでは潜在変数に標準正規分布を仮定しているので、標準正規分布からランダムに潜在変数をサンプリングし、学習済みVAEのデコーダで、画像を生成することができました。
VQ-VAEでは潜在変数の分布がわからないので、それを知る必要があります。
そこで、論文ではPixelCNNという画像の生成モデルで潜在変数の分布を学習します。
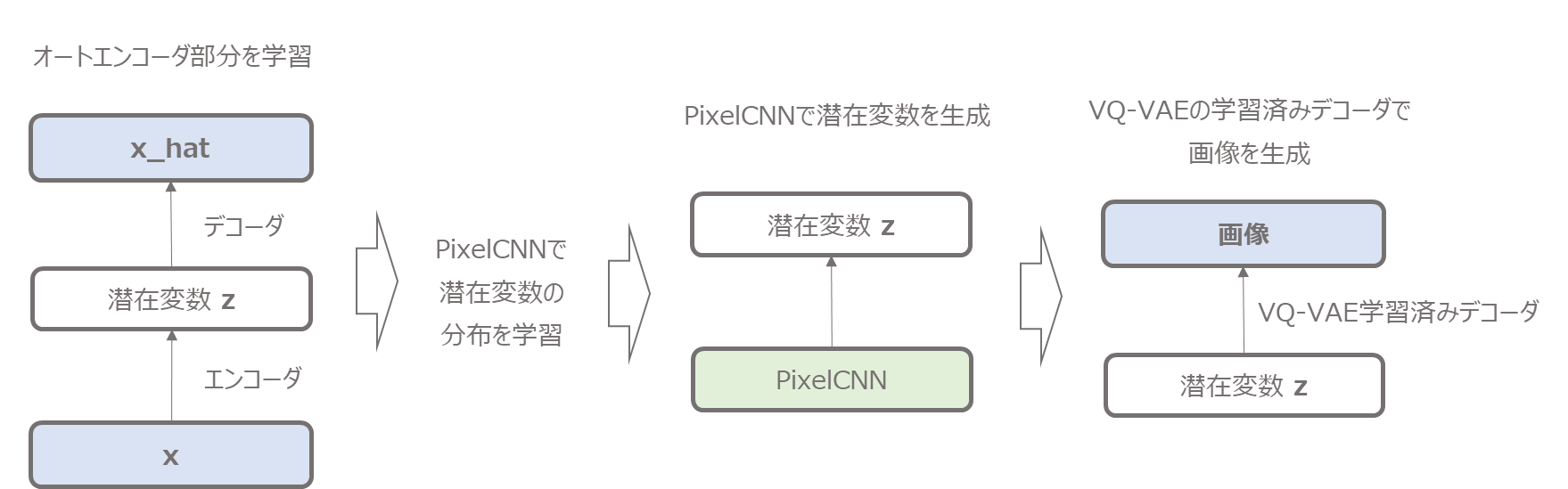
潜在変数の空間なので、もとの画像よりも低次元であり学習が簡単です。
そしてその学習したPixelCNNでランダムに潜在変数を生成し、学習済みのVQ-VAEのデコーダで画像を生成します。
今回の記事では、オートエンコーダ部分の実装のみですので、PixelCNNを含めた画像生成はまたの機会にしたいと思います。
PixelCNN自体の解説実装はこちらでしています。
データについて
データは以下のようなスクレイピングしてきたドラクエ画像を使用します。

ただ、ちゃんとした画像だけだとサンプル数が少なかったため、Google検索でもう少し幅広に集めました。
以下のような画像です。
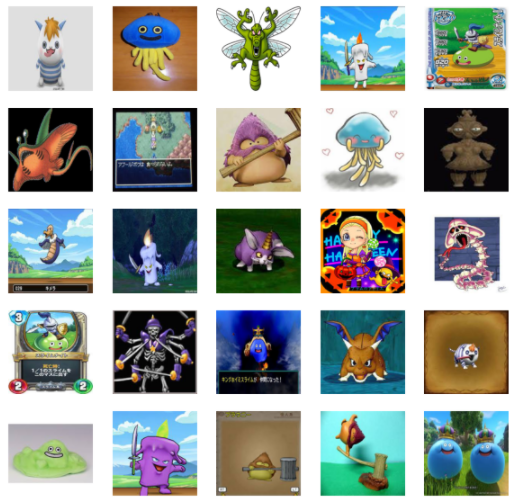
結構関係のない画像や学習にはいまいちな画像も含まれていたため、そこは目で見て落としていきました(除き切れていない、あまり良くない画像もありますね…)。
現状は学習データとして5000枚弱ぐらいあります。
もう少しスクレイピングしているので、将来的は1~2万枚ぐらいまでは増やしたいと思っています。
VQ-VAEの実装
では、まず必要なライブラリをインストールしていきましょう。
# PyTorch関連 import torch import torch.nn as nn import torch.nn.functional as F # 描画など import matplotlib.pyplot as plt import numpy as np
モデル
次のような形で実装していきます。
インプット
↓
デコーダ
↓
pre_conv(潜在変数の一歩手前を計算する畳み込み層)
↓
Vector Quantizer(埋め込みベクトルへのマッピング)
↓
デコーダ
↓
アウトプット
という順です。

では、順に作成していきましょう。
残差結合
まず、エンコーダ、デコーダでは残差結合を使いますので、先に残差結合層を作成しておきます。
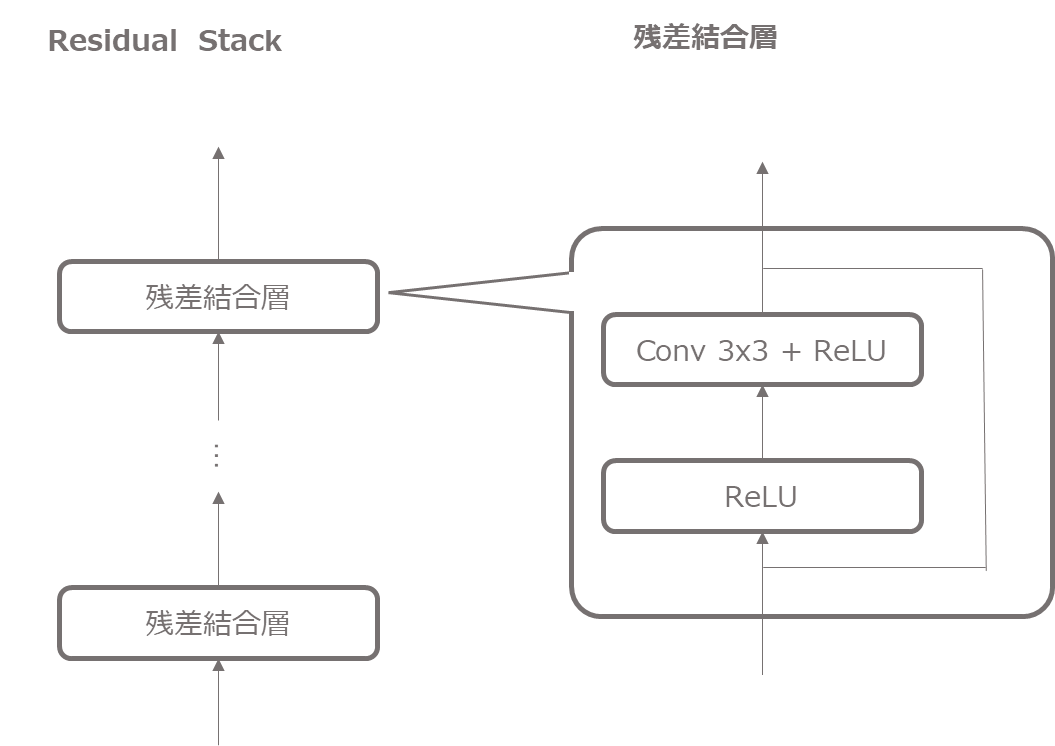
class Residual(nn.Module):
def __init__(self, in_channels, hidden_dim, num_residual_hiddens):
super(Residual, self).__init__()
self.conv_1 = nn.Conv2d(in_channels=in_channels,
out_channels=num_residual_hiddens,
kernel_size=3,
stride=1,
padding=1)
self.conv_2 = nn.Conv2d(in_channels=num_residual_hiddens,
out_channels=hidden_dim,
kernel_size=1,
stride=1)
def forward(self, x):
h = torch.relu(x)
h = torch.relu(self.conv_1(h))
h = self.conv_2(h)
return x + h # 残差結合
そして、この残差結合を複数積み重ねますので、ResidualStackというクラスを作成します。
ここでは、nn.ModuleListを使って、num_residual_layers分だけ残差結合層をスタックします。
class ResidualStack(nn.Module):
def __init__(self, in_channels, hidden_dim, num_residual_layers, num_residual_hiddens):
super(ResidualStack, self).__init__()
self._num_residual_layers = num_residual_layers
# 複数の残差結合をスタックする
self._layers = nn.ModuleList(
[Residual(in_channels, hidden_dim, num_residual_hiddens)
for _ in range(self._num_residual_layers)]
)
def forward(self, x):
for i in range(self._num_residual_layers):
x = self._layers[i](x)
return F.relu(x)
エンコーダ
続いてエンコーダです。
エンコーダは以下のような仕組みになります。
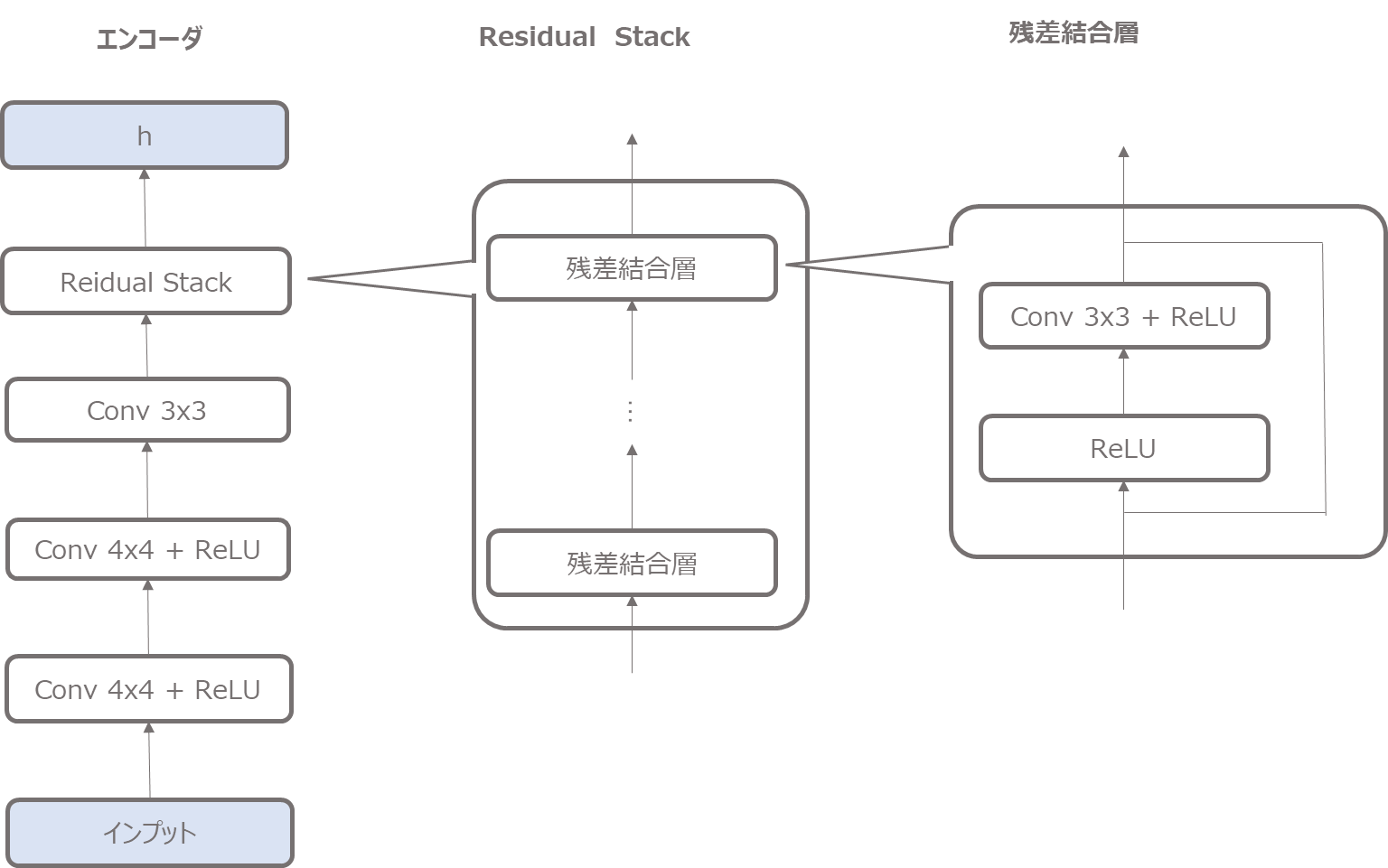
複数の畳み込み層と先ほど作成した残差結合のresidual stack層で構成されています。
上図のような順で計算し、最終的に潜在変数にマッピングするための\({\bf{z}}_e\)を計算します。
実装では以下のようになります。
class Encoder(nn.Module):
def __init__(self, in_channels, hidden_dim, num_residual_layers, residual_hidden_dim, name=None):
super(Encoder, self).__init__()
self._in_channels = in_channels
self._hidden_dim = hidden_dim
self._num_residual_layers = num_residual_layers
self._residual_hidden_dim = residual_hidden_dim
self._enc_1 = nn.Conv2d(in_channels, hidden_dim // 2,
kernel_size=4,
stride=2,
padding=1
)
self._enc_2 = nn.Conv2d(hidden_dim //2, hidden_dim,
kernel_size=4,
stride=2,
padding=1
)
self._enc_3 = nn.Conv2d(hidden_dim, hidden_dim,
kernel_size=3,
stride=1,
padding=1
)
self._residual_stack = ResidualStack(
hidden_dim,
hidden_dim,
num_residual_layers,
residual_hidden_dim,
)
def forward(self, inputs):
h = torch.relu(self._enc_1(inputs))
h = torch.relu(self._enc_2(h))
h = self._enc_3(h) # ResidualStackの中にReLUが入っている
return self._residual_stack(h)
デコーダ
次にデコーダです。
デコーダは潜在変数\({\bf{z}}_q\)をインプットとして、residual stack、畳み込み層と処理し、最終的に画像\({\bf{x}}\)を復元しようとします。
最後にシグモイド関数で0-1にしています(他のやり方の方が良いかもしれませんが手っ取り早いので…)。
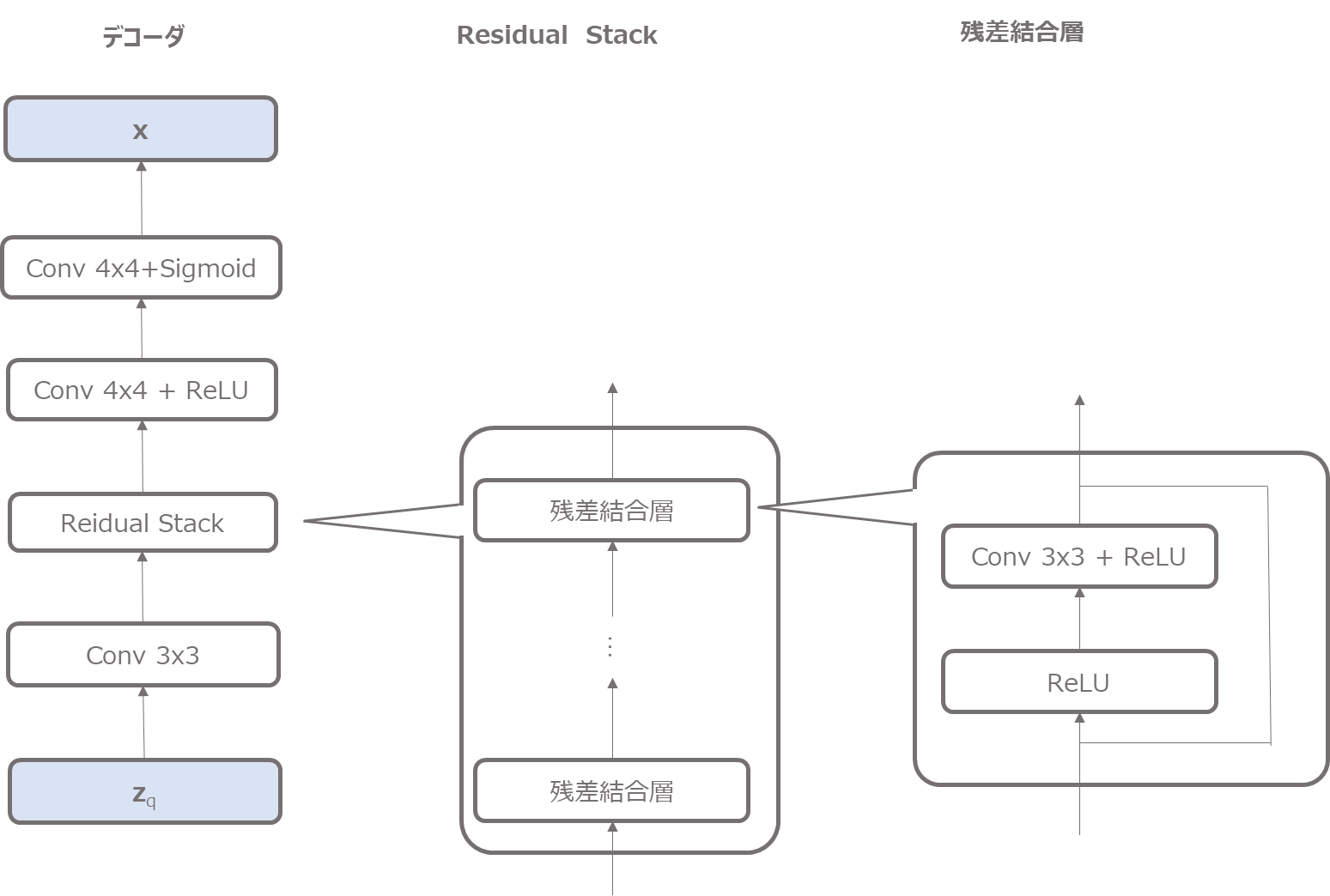
実装はこちらです。
class Decoder(nn.Module):
def __init__(self, in_channels, hidden_dim, num_residual_layers, residual_hidden_dim,
name=None):
super(Decoder, self).__init__()
self._in_channels = in_channels
self._hidden_dim = hidden_dim
self.num_residual_layers = num_residual_layers
self.residual_hidden_dim = residual_hidden_dim
self._dec1 = nn.Conv2d(in_channels, hidden_dim,
kernel_size=3,
stride=1,
padding=1)
self._residual_stack = ResidualStack(hidden_dim,
hidden_dim,
num_residual_layers,
residual_hidden_dim
)
self._dec2 = nn.ConvTranspose2d(hidden_dim, hidden_dim // 2,
kernel_size=4,
stride=2,
padding=1
)
self._dec3 = nn.ConvTranspose2d(hidden_dim // 2, 3,
kernel_size=4,
stride=2,
padding=1
)
def forward(self, encoder_outputs):
h = self._dec1(encoder_outputs)
h = self._residual_stack(h)
h = torch.relu(self._dec2(h))
x_reconstructed = self._dec3(h)
x_reconstructed = torch.sigmoid(x_reconstructed)
return x_reconstructed
離散化
続いて、エンコーダで計算した\({\bf{z}}_e\)から離散化した潜在変数\({\bf{z}}_q\)をマッピングする部分です。
やっていることは以下の図のようにシンプルですが、埋め込みベクトルを選ぶ際には2乗距離が一番近いベクトルを選んでいます。
$$z_q(x)=e_k, \hspace{10pt}\text{where } k=\arg\min_j\|z_e(x)-e_j\|_2$$
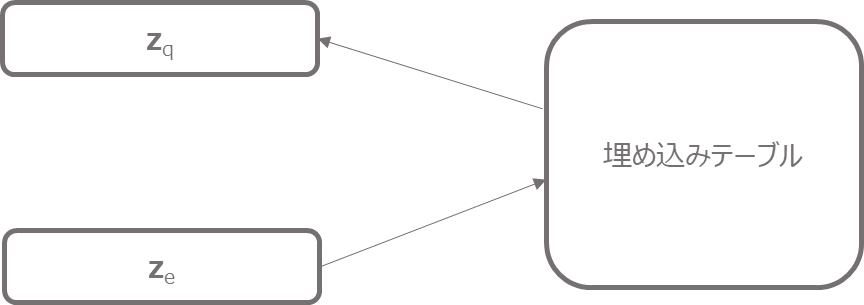
コードは以下です。
class VectorQuantizer(nn.Module):
def __init__(self, embedding_dim, num_embeddings, commitment_cost,
):
super(VectorQuantizer, self).__init__()
self._embedding_dim = embedding_dim
self._num_embeddings = num_embeddings
self._commitment_cost = commitment_cost
# コードブック(ボトルネック)
self._w = nn.Embedding(self._num_embeddings, self._embedding_dim)
self._w.weight.data.uniform_(-1/self._num_embeddings, 1/self._num_embeddings)
def forward(self, inputs):
'''
inputs: N×C×H×W
'''
# N×C×H×WをN×H×W×Cに変換する. (Cは埋め込みベクトルの次元)
inputs = inputs.permute(0, 2, 3, 1).contiguous()
input_shape = inputs.size()
input_flattened = inputs.view(-1, self._embedding_dim) # すべて縦に並べる
distances = (torch.sum(input_flattened ** 2, dim=1, keepdim=True)
- 2 * torch.matmul(input_flattened, self._w.weight.t())
+ torch.sum(self._w.weight ** 2, dim=1))
encoding_indices = torch.argmax(-distances, 1).unsqueeze(1)
# one-hotベクトルに変換
encodings = torch.zeros(encoding_indices.shape[0], self._num_embeddings, device=inputs.device)
encodings.scatter_(1, encoding_indices, 1) # one-hot
# 埋め込み表現を取得し、元のインプットの形に戻す。
quantized = torch.matmul(encodings, self._w.weight) # one-hot ⇒ ベクトル
quantized = quantized.view(input_shape)
# 損失の計算
# 二乗誤差で計算. sgの部分はdetach()で勾配を計算しないようにする
e_latent_loss = F.mse_loss(quantized.detach(), inputs)
q_latent_loss = F.mse_loss(quantized, inputs.detach())
loss = q_latent_loss + self._commitment_cost * e_latent_loss
# sgの部分はdetach()で勾配を計算しない
quantized = inputs + (quantized - inputs).detach()
quantized = quantized.permute(0, 3, 1, 2).contiguous()
# perplexityを計算
avg_probs = torch.mean(encodings, dim=0)
perplexity = torch.exp(-torch.sum(avg_probs * torch.log(avg_probs + 1e-10)))
return {'distances': distances,
'quantize': quantized,
'loss': loss,
'encodings': encodings,
'encoding_indices': encoding_indices,
'perplexity': perplexity}
slef._wが埋め込みベクトルになります。
input_flattenedとしているところは、\(N\times H\times W\)のすべてのセルを縦に並べて、すべての\({\bf{e}}_j\)との距離を一気に計算しています(賢い計算方法ですね)。
そして、距離が最も近い埋め込みベクトルを選び、潜在変数\({\bf{z}}_q\)を計算しています。
最後に以下の式で損失関数の値を計算しています。
$$L=\log p\left(x|z_q(x)\right) + \left\|\text{sg}[z_e(x)]-e \right \|^2_2 + \beta \left\|z_e(x)-\text{sg}[e]\right\|^2_2$$
VQ-VAE全体
以下でエンコーダ、デコーダ、pre_vq_conv(エンコーダのアウトプットを処理する畳み込み層)、Vector Quantizerを合わせたVQ-VAE全体を作成します。
class VQVAE(nn.Module):
def __init__(self, encoder, decoder, vqvae, pre_vq_conv1,
data_variance, name=None):
super(VQVAE, self).__init__()
self._encoder = encoder
self._decoder = decoder
self._vqvae = vqvae
self._pre_vq_conv1 = pre_vq_conv1
self._data_variance = data_variance
def forward(self, inputs):
z = self._pre_vq_conv1(self._encoder(inputs)) # zの事前分布
vq_output = self._vqvae(z)
x_reconstructed = self._decoder(vq_output['quantize'])
reconstructed_error = torch.mean(torch.square(x_reconstructed - inputs) / self._data_variance)
loss = reconstructed_error + vq_output['loss']
return {
'z': z,
'x_reconstructed': x_reconstructed,
'loss': loss,
'reconstructed_error': reconstructed_error,
'vq_output': vq_output
}
モデルを作成
モデルを作成する関数を定義します。
エンコーダ、デコーダ、pre_vq_conv1、VectorQuantizerをそれぞれインスタンス化し、VQVAEクラスに渡すことでモデルを作成します。
def create_vqvae_model():
encoder = Encoder(in_channels=3,
hidden_dim=HIDDEN_DIM,
num_residual_layers=NUM_RESIDUAL_LAYERS,
residual_hidden_dim=RESIDUAL_HIDDEN_DIM)
decoder = Decoder(in_channels=EMBEDDING_DIM,
hidden_dim=HIDDEN_DIM,
num_residual_layers=NUM_RESIDUAL_LAYERS,
residual_hidden_dim=RESIDUAL_HIDDEN_DIM)
pre_vq_conv1 = nn.Conv2d(HIDDEN_DIM,
EMBEDDING_DIM,
kernel_size=1,
stride=1)
vqvae = VectorQuantizer( # EMAを使わない方
embedding_dim=EMBEDDING_DIM,
num_embeddings=NUM_EMBEDDINGS,
commitment_cost=COMMITMENT_COST,
)
# モデル
model = VQVAE(encoder=encoder,
decoder=decoder,
vqvae=vqvae,
pre_vq_conv1=pre_vq_conv1,
data_variance=train_data_variance)
# オプティマイザ
optimizer = torch.optim.Adam(model.parameters(), lr=LEARNING_RATE)
return model, optimizer
学習
では、ハイパーパラメータを設定します。
BATCH_SIZE = 32 IMAGE_SIZE = 32 HIDDEN_DIM = 128 RESIDUAL_HIDDEN_DIM = 32 NUM_RESIDUAL_LAYERS = 2 EMBEDDING_DIM = 32 # 各bottle-neckは64次元 NUM_EMBEDDINGS = 128 # いわゆるK. K種類のbottle-neckがある COMMITMENT_COST = 0.25 USE_EMA = False DECAY = 0.99 LEARNING_RATE = 3e-4 # 論文では少し小さめの2e-4
エポック数を200にして計算します。
損失等の値は必要に応じて表示してください。
model, optimizer = create_vqvae_model() # モデルの作成
train_res_recon_error, train_res_perplexity = [], []
val_res_recon_error, val_res_perplexity = [], []
device = 'cuda'
num_epochs = 200
model.to(device)
model.train()
for epoch in range(num_epochs):
for i, data in enumerate(train_loader):
data = data.to(device)
results = model(data)
optimizer.zero_grad()
loss = results['loss']
loss.backward()
optimizer.step()
実行結果
以下のように学習が進んでいきます。
1エポック目終了時点ではモノクロ画像のようになっています。

次に10エポック目終了時です。

色もだいぶついてきて、どのモンスターかは十分わかります。
続いて、20エポック目終了時です。

もう元の画像とあまり変わらないレベルになってきました。
200エポック終了した時点では、非常にきれいな画像になりました。

ドラクエI~ドラクエVIIまでの画像をに学習データにして、ドラクエVIIIとドラクエIXの画像をテストデータにしていますが、上記のモンスターは学習データにもありそうです。
なので、ドラクエIXに初めて登場した画像も含めて見てみたところ、以下のようにうまくいっていることが確認できました(ドラクエVII以前の画像も混ざっています)。
複雑な画像もうまく再構築できていることがわかります。

まとめ
今回はPyTorchでVQ-VAEのオートエンコーダ部分を実装しました。
次は、PixelCNNなどの生成モデルで潜在変数の分布を学習して、VQ-VAEにより画像を生成するということをやってみたいと思います。
では!


