【PyTorch】Conditional VAEを実装する

前回は以下の記事でPyTorchを使ってVAE(Variational Auto-Encoder)を実装しました。

: 【PyTorch】VAE(Variational Auto-Encoder)を実装する
さて、以前こちらの記事ではVAE(Variational Auto-Encoder)の解説およびTensorflowを使った実装をしました。 https://data-analytics.fun/20 ...

今回は、VAE(Variational Auto-Encoder)の派生であるConditional VAEを使って、ラベルにもとづいた画像を生成したいと思います。

データセットは今回もMNISTのデータを使いたいと思います。

他のモデルで他のデータセットを使ってラベルにもとづいた画像生成する場合の参考になればと思います。

VAEの詳細については上記の記事を、さらに詳細については以下の記事をご参照ください(通常のVAEを実装していた方が理解は簡単です)。

: 【Python (Tensorflow) による実装付き】Variational Auto-Encoder (VAE) を理解する
今回は、2014年に提案された画像生成モデル “Variational Auto-Encoder (VAE) ” について解説していきたいと思います。仕組みの詳細まで踏み込んでいるため、計算などが複 ...

では、さっそく見ていきましょう。

1 通常のVAEとConditinal VAEの違い
2 実装
3 まとめ

通常のVAEとConditinal VAEの違い

通常のVAEとConditinal VAEの違いは、条件付けするラベルをエンコーダ、デコーダそれぞれのインプットとして渡すか渡さないかの違いです。

以下の図の左側が通常のVAEで、右側がConditional VAEです。

Conditional VAEはインプットを${\bf{x}}$とラベルを連結したものにします。

同様にデコーダのインプットも潜在変数${\bf{z}}$にラベルを連結したものになります。

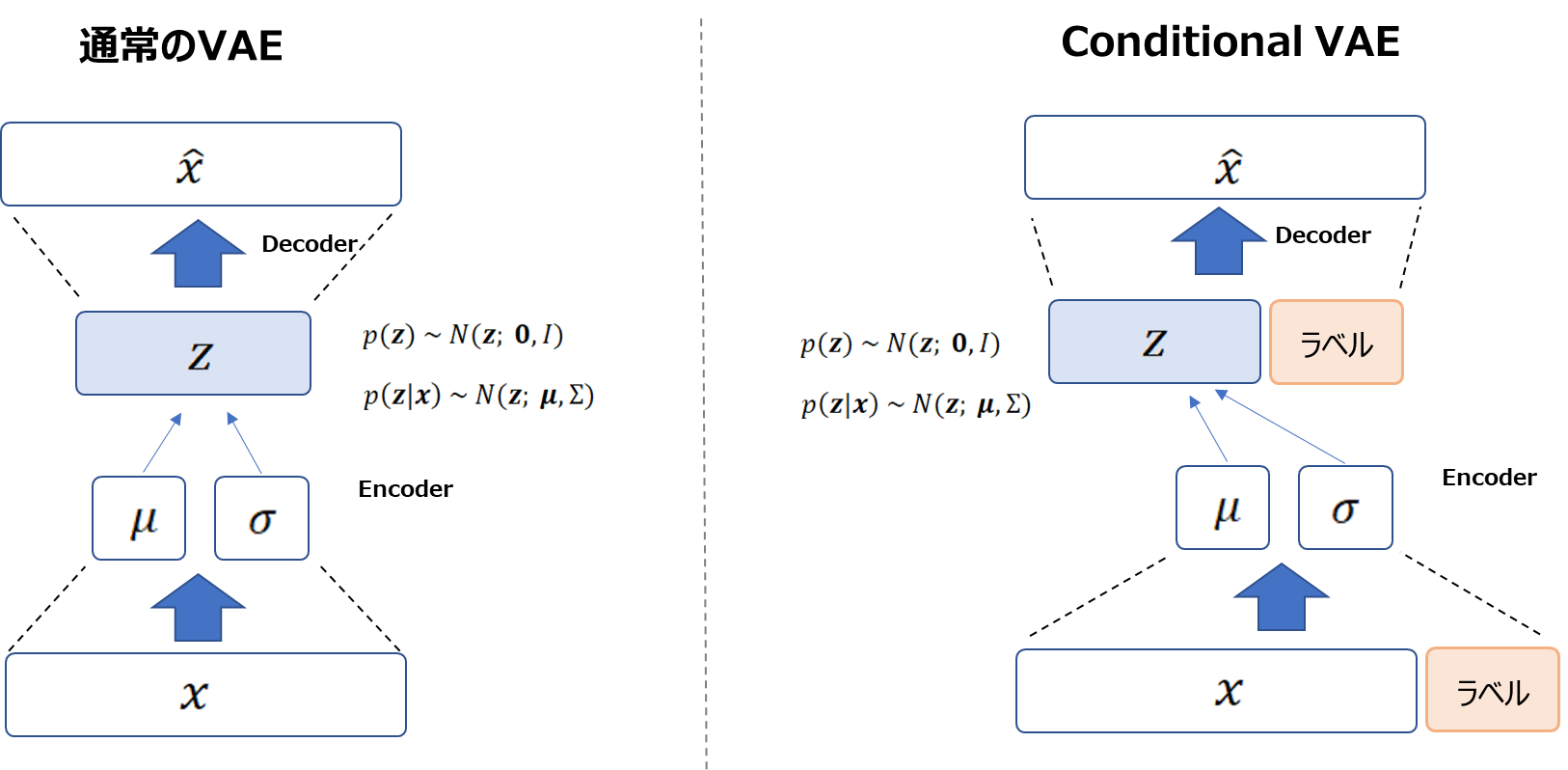
ラベルは、数値などのカテゴリ変数であればone-hot表現になります。

損失関数などはまったく同じですので、実装も大きく変わることはありません。

では実装を見ていきましょう。

実装

まずは必要なモジュールをインポートします。

# PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F

# データセット用
import torchvision
import torchvision.transforms as transforms

# 描画用
import matplotlib.pyplot as plt
import numpy as np

データセットを準備します。

batch_size = 128

train_dataset = torchvision.datasets.MNIST(
    root='./data',
    train=True,
    transform=transforms.ToTensor(),
    download=True,
)
train_loader = torch.utils.data.DataLoader(
    dataset=train_dataset,
    batch_size=batch_size,
    shuffle=True,
    num_workers=0
)

エンコーダ

画像から潜在変数に変換するエンコーダを作成します。

通常のVAEと違うところは、画像データ${\bf{x}}$にラベルをone-hotエンコーディングして連結し、その連結した変数を全結合で処理している点です。

class Encoder(nn.Module):
  def __init__(self, input_dim, hidden_dim, latent_dim, num_lables):
    super(Encoder, self).__init__()
    self.num_labels = num_labels
    self.fc = nn.Linear(input_dim+self.num_labels, hidden_dim)
    self.fc_mu = nn.Linear(hidden_dim, latent_dim)
    self.fc_var = nn.Linear(hidden_dim, latent_dim)
 
  def forward(self, x, label):
    # ラベル
    label_onehot = torch.zeros(label.shape[0], self.num_labels).to(device)
    label_onehot.scatter_(1, label.unsqueeze(1), 1.0)
    x_cat = torch.cat((x, label_onehot), dim=-1)

    # ニューラルネットワーク
    h = torch.relu(self.fc(x_cat))1
    mu = self.fc_mu(h)
    log_var = self.fc_var(h)

    eps = torch.randn_like(torch.exp(log_var))
    z = mu + torch.exp(log_var / 2) * eps
    return mu, log_var, z

デコーダ

続いて潜在変数から画像を生成するデコーダです。

デコーダもエンコーダと同様に、潜在変数だけでなくラベルをone-hotエンコーディングしたものを連結しインプットとします。

VAEと違う箇所をハイライトしています。

class Decoder(nn.Module):
  def __init__(self, input_dim, hidden_dim, latent_dim, num_labels):
    super(Decoder, self).__init__()
    self.num_labels = num_labels
    self.fc = nn.Linear(latent_dim+self.num_labels, hidden_dim)
    self.fc_output = nn.Linear(hidden_dim, input_dim)
    
  def forward(self, z, label):
    # ラベル
    label_onehot = torch.zeros(label.shape[0], self.num_labels).to(device)
    label_onehot.scatter_(1, label.unsqueeze(1), 1.0)
    z_cat = torch.cat((z, label_onehot), dim=-1)
    h = torch.relu(self.fc(z_cat))
    output = torch.sigmoid(self.fc_output(h))
    return output

Conditional VAE全体

モデル全体はVAEと同様にエンコーダとデコーダをつなげるだけです。

class CVAE(nn.Module):
  def __init__(self, input_dim, hidden_dim, latent_dim, num_labels):
    super(CVAE, self).__init__()
    self.encoder = Encoder(input_dim, hidden_dim, latent_dim, num_labels)
    self.decoder = Decoder(input_dim, hidden_dim, latent_dim, num_labels)
   
  def forward(self, x, label):
    mu, log_var, z = self.encoder(x, label)
    x_decoded = self.decoder(z, label)
    return x_decoded, mu, log_var, z

損失関数

損失関数はVAEとまったく同じで、以下の下界を最大化します。

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta)&= \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] - D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

def loss_function(label, predict, mu, log_var):
  reconstruction_loss = F.binary_cross_entropy(predict, label, reduction='sum')
  kl_loss = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
  vae_loss = reconstruction_loss + kl_loss
  return vae_loss, reconstruction_loss, kl_loss

学習

ハイパーパラメータを設定します。

image_size = 28 * 28
h_dim = 64
z_dim = 32
num_labels = 10
num_epochs = 30
learning_rate = 1e-3

モデルを作成します。

device = 'cuda'
model = CVAE(image_size, h_dim, z_dim, num_labels).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

最後に以下のコードで学習を行います。

losses = []
model.train()
for epoch in range(num_epochs):
  train_loss = 0
  for i, (x, labels) in enumerate(train_loader):
    x = x.to(device).view(-1, image_size)
    x = x.to(torch.float32)
    labels = labels.to(device)
    x_recon, mu, log_var, z = model(x, labels)
    loss, recon_loss, kl_loss = loss_function(x, x_recon, mu, log_var)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (i+1) % 100 == 0:
      print(f'Epoch: {epoch+1}, loss: {loss: 0.4f}, reconstruct loss: {recon_loss: 0.4f}, KL loss: {kl_loss: 0.4f}')
  losses.append(loss)

学習が終わったら、実際に画像を生成してみましょう。

標準正規乱数を発生させ、それとラベルを与えることにより数字の画像を生成することができます。

labels = torch.tensor(np.tile(np.arange(10), 5)).to(device)
model.eval()
with torch.no_grad():
  z = torch.randn(50, z_dim).to(device)
  out = model.decoder(z, labels)
out = out.view(-1, 28, 28)
out = out.cpu().detach().numpy()

では、結果を描画してみましょう。

fig, ax = plt.subplots(nrows=5, ncols=10, figsize=(20, 10))
plt.gray()
for i in range(50):
  idx = divmod(i, 10)
  ax[idx].imshow(out[i])
  ax[idx].axis('off');   
fig.show()

以下のような画像が生成されました。