今回は、Transformerの改良版であるTransformer-XLの論文を読んでみたので、詳しく見ていきたいと思います。
Transformer-XLは“Transformer Extra Large”の略で、通常のTransformerと比べて長い文章の依存関係を捉えられるモデルになっています。BERTを超えたXL-Netというモデルでもこの仕組みが使われています。
Transformer-XLでは、一つの文章を複数のセグメントに分けます。なぜ、分けるかというとTransformerの仕組みでは(Dot-Product Attentionの計算部分)、計算量が文章の長さの2乗に比例して多くなるからです。これはなかなかやっかいで、200単語ぐらいであればさくさく動くのですが、2000単語のような長文になると非常に遅くなります。
そこで、文章を複数の短めの文章にわけて、モデルを構築するわけです。その際に過去のセグメントの情報を保持できように工夫がされています。
Transformerについては、こちらをご参照ください。
目次
Transformer-XLの概要
もともと提案されていたセグメントに分けたTransformerは、以下のように、セグメントごとに分けて、その中でモデルを学習する方法を取っています。
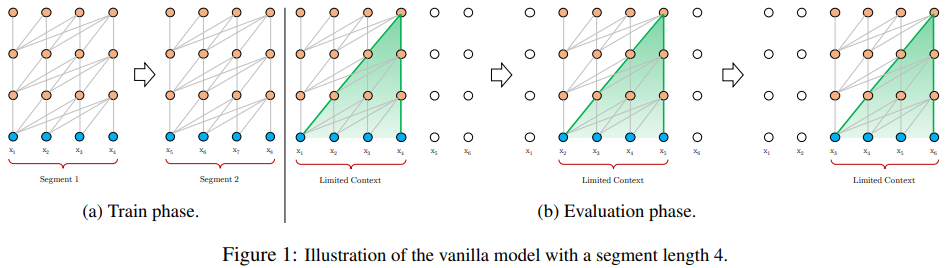
しかしながら、 この方法だと以下のような2点の問題が指摘されています。
- セグメントごとに情報が途切れるため、Transformerが持つ長期の依存関係を捉えられるという利点をいかすことができない。
- 文章の意味や構文を考えず、一定の長さでセグメントを分けるので、必要な情報が失われてしまう。(Context Fragmentation Problem)
では、これらに対応するため、セグメントに分けずにすべての文章を入れればよいのではないかというと、Transformerは文章の2乗に比例して計算負荷が大きくなるので、あまりに長い文章は現実的ではありません。
そこで、Transformer-XLでは以下の2つの工夫を加え、これを改良しました。
- Recurrence Mechanism
各セグメントについて再帰的に処理を行う。 - Relative Positional Encoding
絶対的な位置情報を与えるのではなく、attention計算時にqueryの単語の位置から、keyの相対的な位置情報を与える。
これらの仕組みにより、Transformer-XLでは、長い文章の依存関係を捉えることができ、非常に良い精度が出ました。
Transformer-XLの仕組み
では、この2つをこれから説明したいと思います。
Recurrence Mechanism
Transformer-XLは以下の図のような形で、セグメントを再帰的に処理することでセグメント間に依存関係を持たせます。これをRecurrence Mechanismと呼んでいます。また、セグメントを処理する際はその前のセグメントの情報は完全に固定します。
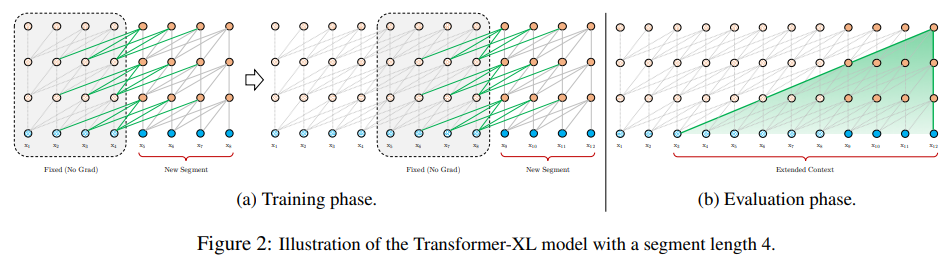
では、式を確認していきましょう。まず、2つのセグメントを考えます。各セグメントの長さは同じで$L$とし、その単語列を\(s_{\tau}=\left[x_{\tau, 1}, x_{\tau, 2}, \cdots, x_{\tau, L} \right]\)と \(s_{\tau+1}=\left[x_{\tau+1, 1}, x_{\tau +1 , 2}, \cdots, x_{\tau +1 , L} \right]\)とします。\(\tau\)はセグメントの番号を表します。
そして、\(\tau\)番目のセグメント、\(n\)番目のレイヤーの隠れ層の値を\(h^n_\tau \in \mathbb{R}^{L\times d}\)と表します。
このとき、\(\tau+1\)番目のセグメント、\(n\)番目のレイヤーの隠れ層の値 \(h^n_\tau \in \mathbb{R}^{L\times d}\)は、以下のように計算されます。
$$\begin{align}
\tilde {h} ^{n -1 }_{\tau + 1}&= \left[\text{SG}\left( h^{n-1}_\tau \right)\circ h ^{n -1 }_{\tau + 1} \right] \\
q^n_{\tau +1}&= h^{n-1}_{\tau +1}W_q^T \\
k^n_{\tau +1}&= \tilde{h}^{n-1}_{\tau +1}W_k^T \\
v^n_{\tau +1}&= \tilde{h}^{n-1}_{\tau +1}W_v^T \\
\tilde {h} ^{n -1 }_{\tau + 1}&=\text{Transformer-Layer}\left( q^n_{\tau +1} ,
k^n_{\tau +1} , v^n_{\tau +1} \right)
\end{align}$$
\(\text{SG}\)はstop-gradientの略で、更新しないというとを意味しており、\(\left[h_u \circ h_v \right]\)は行方向に2つの隠れ層を連結することを意味します。
1つめの式は、セグメント\(\tau\)、つまり前のセグメントの一つ下のレイヤーの隠れ層と、セグメント\(\tau+1\)の一つしたのレイヤーの隠れ層を結合したものを、一つの隠れ層としています。
2行目は、queryなので何から注意を向けるか?を意味していますので、それには自分自身のセグメント\(\tau+1\)の一つ前のレイヤーの隠れ層を使います。
3行目、4行目は、key-valueペアなのでqueryからどこに注意を向けるか?を意味するので、それには、自分自身であるセグメント\(\tau+1\)の一つ前のレイヤーの隠れ層と、前のセグメントの隠れ層を結合した\( \tilde {h} ^{n -1 }_{\tau + 1} \)を使います。
そして、そのquery、key-valueをTransformerに入れて、次の隠れ層の値を計算するというものです。
これにより、前のセグメントの情報を次のセグメントに引き継ぐことができます。
また、上記では一つ前のセグメントの情報のみを引き継いでいましたが、\(h^{n-1}_\tau\)を複数のセグメントから取ってくることで、それ以前の情報を引き継ぐことが可能です。これを\(m^n_\tau\in \mathbb{R}^{M\times d}\)として、長さ\(M\)の隠れ層とします。
Relative Positional Encoding
Recurrence Mechanismでは、前の層の隠れ層の値 \(h^{n-1}_\tau \) を再利用することで高速化を図ります。この場合、Positional Encodingまで再利用してしまうとうまくいきません。
つまり、Positional Encodingを\(U\in \mathbb{R}^{L_{\text{max}}\times d}\)、 セグメント\(\tau\)での単語の埋め込みを\(E_{S_{\tau} }\in \mathbb{R}^{L \times d}\) として、
$$\begin{align}
h_{\tau+1} &= f\left(h_\tau, E_{S_{\tau+1}} + U_{1:L} \right) \\
h_{\tau} &= f\left(h_{\tau-1}, E_{S_\tau} + U_{1:L} \right)
\end{align}$$
とすると、別のセグメントに同じ位置情報を使ってしまい、情報を失ってしまいます。そこで、“Relative Positional Encoding”を使います。
Self-Attentionにおいては、どこからどこに注意を向けるか、を考えますが、別に絶対的な位置でなくても、queryの単語から相対的にいくつ前という情報で十分だということを使います。つまり、セグメント\(\tau\)の\(i\)番目の単語である\(\text{query}_{\tau, i}\)から、それ以前の単語である\(\text{key}_{\tau, \le i}\)へ注意を向ける場合、 \(\text{key}_{\tau, j}\) の\(j\)という絶対位置ではなく、queryの単語から\(i-j\)前という相対位置がわかれば十分です。
そこで、そのrelative positional encodingを\(R\in \mathbb{R}^{L_{\text{max}\times d}}\)として、モデルに組み込みます。
では、従来のattentionとの違いを見てみましょう。
まず、\(\tilde{Q}=QW_q^T\)、 \(\tilde{K}_i=KW_k^T\) とします。
従来の絶対的な(absolute)encdoingによるattentionは、\(\tilde{Q}\tilde{K}^T\)の\(i\), \(j\) 番目の要素なので以下のように計算できます。(論文では何がベクトルで何が行列かわかりにくかったので、表記を少し変えています。太字がベクトルです)
$$\begin{align}
A_{i,j}^{\text{abs}} &=\left(\tilde{Q}\tilde{K} ^T\right)_{i, j} = {\bf{q}}_i^TW_q^T \left( {\bf{k}}_i^T W_k ^T \right)^T= \left({\bf{e}}^T_{x_i}+{\bf{u}}_i^T\right) W_q^T W_k\left({\bf{e}}_{x_j}+{\bf{u}}_j\right) \\
&= {\bf{e}}_{x_i}^T W_q^T W_k {\bf{e}}_{x_j} + {\bf{e}} _{x_i}^TW_q^TW_k {\bf{u}} _j
+{\bf{u}}_i^TW_q ^T W_k {\bf{e}} _{x_j} + {\bf{u}} _i ^T W_q ^T W_k {\bf{u}} _j
\end{align}$$
では、1項目を(a)、2項目を(b)、3項目を(c)、4項目を(d)として、それぞれがrelative positional encodingの場合にどのように変わるかみていきたいと思います。
(a) \( {\bf{e}}_{x_i}^TW_q^T W_ke_{x_j} \) ⇒ \( {\bf{e}}_{x_i}^T W_q^T W_{k, E} {\bf{e}}_{x_j} \)
ここは大きく変わらず \(W_k\)が\(W_{k, E} \)になっているだけです。keyのパラメータのうちEmbeddingした情報にかかる部分という意味です。
(b) \( {\bf{e}}_{x_i}^TW_q^T W_k {\bf{u}}_j \) ⇒ \( {\bf{e}}_{x_i}^T W_q^T W_k {\bf{r}}_{i-j} \)
Positional Encoding \( {\bf{u}} _j \)が相対的なpositional encoding \( {\bf{r}}_{i-j} \)になります。また、\( W_k \)もrelative positional encoding用に\( W_{k, R} \) に変えておきます。
(c)\({\bf{u}}_i^T W_q^T W_k {\bf{e}} _{x_j} \) ⇒ \({\bf{u}}^T W_{k, E}{\bf{e}}_{x_{j}}\)
\( W_k \)が\(W_{k, E} \)になっているのは(a)と同じです。\({\bf{u}}_i \)が \({\bf{u}}\)というベクトルに変わっていますが、相対的なpositional encodingを考えた場合、query部分のpositional encodingは位置に依存しないように固定して(\(i\)とは独立にして)、key部分で調整するという考え方によるものです。ですので、 \({\bf{u}}_i \) が \({\bf{u}}\) という位置に依存しないベクトルに変わています。
(d)\({\bf{u}} _i^T W_q^T W_k {\bf{u}}_j\) ⇒ \({\bf{v}}^TW_{k, R} {\bf{r}} _{i-j}\)
(c)と同じでquery部分は位置に依存しないように\(v\)というベクトルで置き換えています。そして、keyの方は、\( {\bf{u}} _j\)が\( {\bf{r}} _{i-j}\)とrelative positional encodingにして調整します 。
その結果、attentionスコアは、以下のようになります。
$$\begin{align}
A_{i,j}^{\text{rel}} &= {\bf{e}}_{x_i}^T W_q^T W_{k, E} {\bf{e}} _{x_j} + {\bf{e}} _{x_i}^T W_q^T W_k {\bf{r}} _{i-j} \\
&+ {\bf{u}} ^T W_{k, E} {\bf{e}} _{x_{j}} + {\bf{v}}^T W_{k, R} {\bf{r}} _{i-j}
\end{align}$$
Transformer-XL
では、あとは今までの議論をもとに、Transformerの式を変形したいと思います。
まずは、前のセグメントをくっつけたkey-value用の隠れ層の値です。ここでは前のセグメントだけでなく、Memoryを\(M\)として必要な長さの隠れ層を使います。
$$ \tilde { {\bf{h} } } ^{n -1 }_{\tau + 1}= \left[\text{SG}\left( {\bf{m}}^{n-1}_\tau \right)\circ {\bf{h} } ^{n -1 }_{\tau + 1} \right] $$
続いて、query、key-valueを作成します。keyとvalueには、先ほど計算した\( \tilde { {\bf{h} } } ^{n -1 }_{\tau + 1} \)を使います。
$$\begin{align}
{\bf{q}}^n_{\tau +1}&= {\bf{h}}^{n-1}_{\tau +1}W_q^T \\
{\bf{k}}^n_{\tau +1}&= \tilde{{\bf{h}}}^{n-1}_{\tau +1}{W^n_{k,E}}^T \\
{\bf{v}}^n_{\tau +1}&= \tilde{{\bf{h}}}^{n-1}_{\tau +1}{W^n_v}^T
\end{align}$$
そして、relative positional encodingによるattentionスコアの計算部分です。
$$\begin{align}
A^n_{\tau, i, j} &= {{\bf{q}}_{\tau, i}^n}^T {\bf{k}} _{\tau, j}^n + { {\bf{q}} _{\tau, i}^n}^T W_{k,R}^n {\bf{r}} _{i-j}
+ {\bf{u}} ^T k_{\tau, j}^n + {\bf{v}} ^TW_{k,R}^n {\bf{r}} _{i-j}
\end{align}$$
最後に、attentionスコアからattentionを計算し、context vectorを求め、レイヤー正規化、Positionwise-Feed-Forwardレイヤーで\(n\)番目のレイヤーのアウトプットである隠れ層の値を計算します。
$$\begin{align}
a^n_\tau &= \text{Masked-Softmax}\left(a^n_\tau\right)v^n_\tau \\
o^n_\tau&=\text{LayerNorm}\left(\text{Linear}\left(a^n_\tau\right)+h^{n-1}_\tau\right) \\
h_\tau^n &= \text{Positionwise-Feed-Forward} \left(o^n_\tau\right)
\end{align}$$
ところで、\(W_{k,R}^n {\bf{r}} _{i-j}\)をすべての\((i, j)\)の組み合わせについて求めなくてはなりません。この場合、計算量は文章の長さの2乗に比例しますが、Appendixでこれを文章の長さに線形になるようにする方法が載っています。
結果
WikiText-103、enwik8、 text8、One Billiion Word、Penn Treebankデータセットを使って学習し、そのパープレキシティを見ています。
まずは、文章が長いWikiText-103データセットです。このデータセットは28,000記事の103Mio.単語あり、1記事当たり平均3600単語だそうです。ですので、長期の依存関係を捉えられているかどうかが、確認できます。
そして見事に、パープレキシティが20.5から18.3に下がっており、SoTAを達成しています。
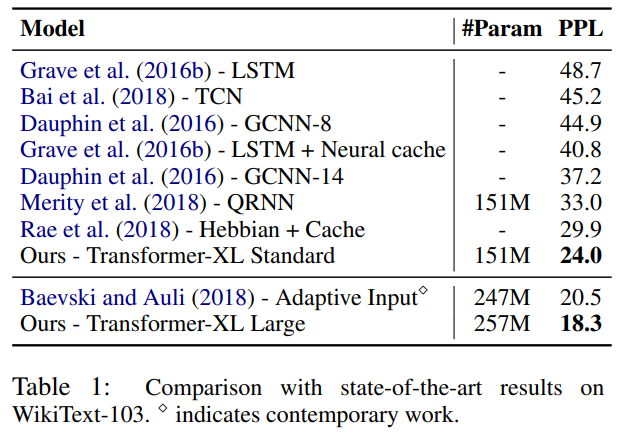
enwiki8データセットでもパープレキシティが下がっていることがわかります。
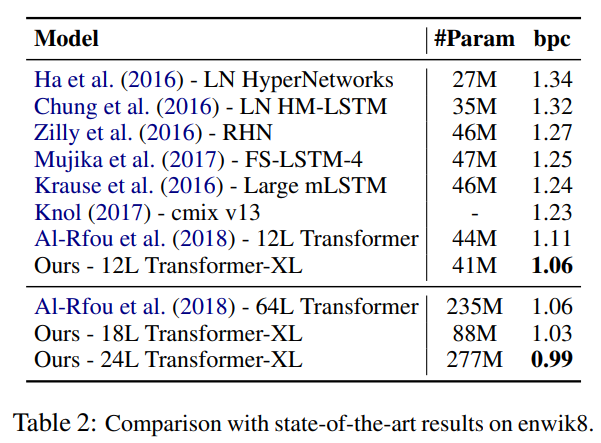
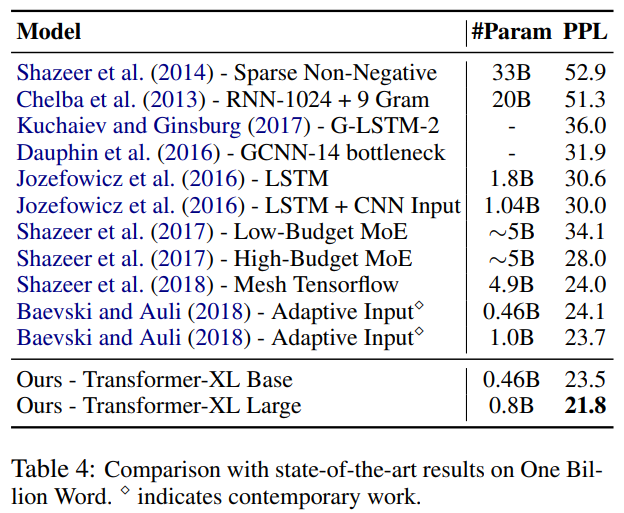
また、One Billion Wordデータセットを見てみましょう。こちらは、文章がシャッフルされているので、1つ1つの文章は短くなっており、長期の依存関係を捉える必要はありません。
こちらでも、パープレキシティが23.7から21.8に減少し、SoTAを達成しており、長文だけでなく短い文章に対しても精度が良いことがわかります。
それ以外にも論文では“Relative Effective Context Length”という尺度を用いた検証や、文章生成の検証などがされていますので、興味のある方は論文を読んでいただければと思います。
まとめ
今回は、Transformer-XLと呼ばれる、長い依存関係を捉えることができるモデルを紹介しました。こちらは、その後、XLNetの仕組みに使われることになります。
では、この知識とBERTの知識を前提に、今後XLNetの論文を読んでみたいと思います!!
