今回はバッチ正規化 (Batch Normalization) に続き、ディープラーニングでは一般的となっている ドロップアウト (Dropout) について解説したいと思います。
ドロップアウトはオーバーフィッティングを減らすことができる非常に有効な手段で、TransformerやBERTなど様々な仕組みの中で使われていますのでしっかりと理解しておきましょう。
原論文はこちらです。
『Dropout: A Simple Way to Prevent Neural Networks from Overfitting』
論文のタイトルにもあるように非常にシンプルなオーバーフィッティングを抑える手法です。
では見ていきましょう。
ドロップアウトの概要
ドロップアウトは簡単にいうとネットワークがオーバーフィッティングするのを抑える仕組みです。
実現方法は非常にシンプルです。
以下の図の左側が通常のニューラル・ネットワークで、右側がドロップアウトを使ったニューラルネットワークです。
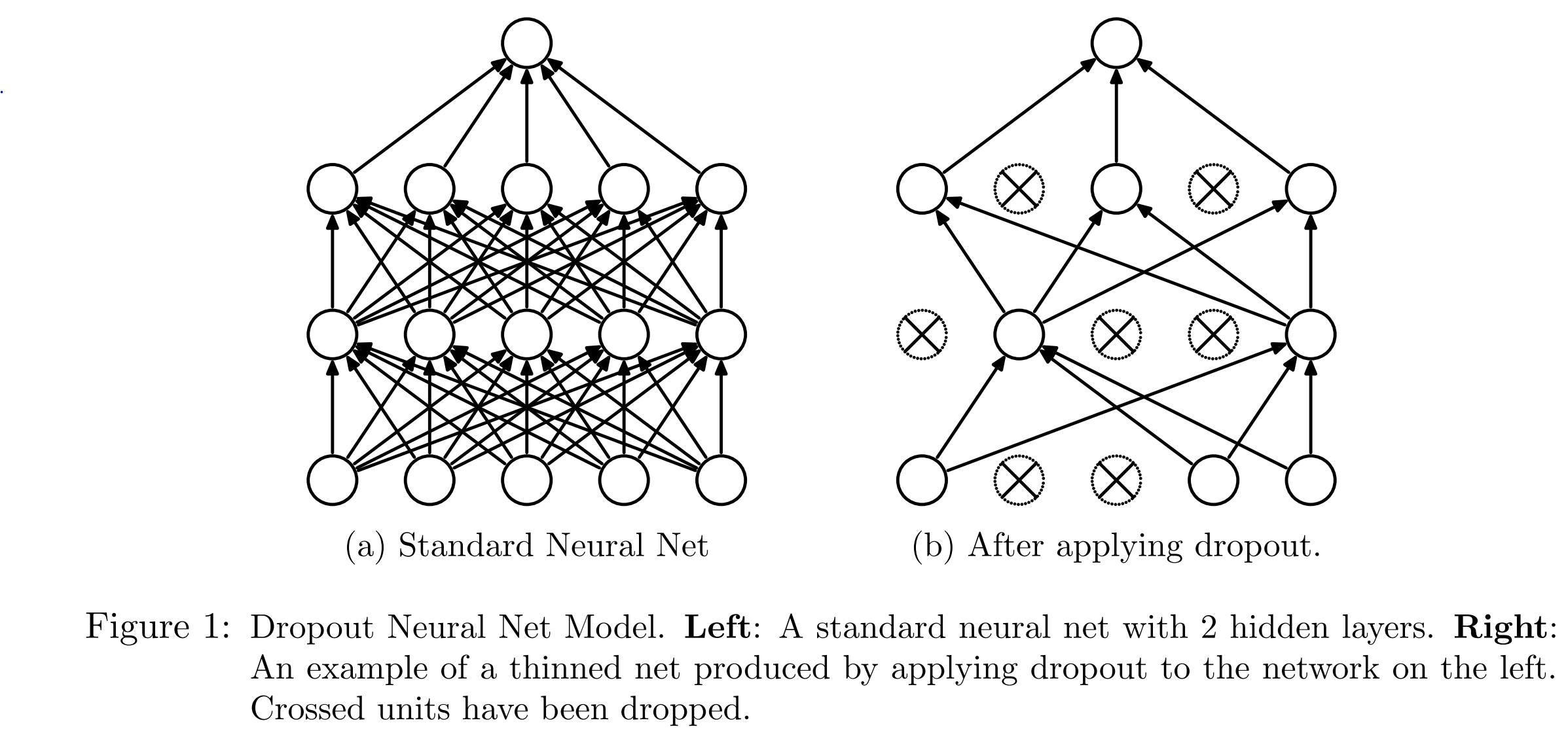
右の方はいくつかのニューロン (ユニット) がバツになって使用されていませんね。
このようにドロップアウトはミニバッチごとに一定の確率で選んだニューロンを使用しないようにします。
この確率をドロップアウト確率と呼びます。
ですので、ミニバッチごと使わないニューロンをランダムに変えていきます。
基本的にこれだけなのですが、より深く理解するためにここからドロップアウトの背景などを詳しく見ていきたいと思います。
ドロップアウトの背景
繰り返しになりますが、ドロップアウトの背景には、ディープラーニングはパラメータが多いためどうしてもオーバーフィッティングしやすいという課題があります。
ディープラーニングはパラメータが多いのでオーバーフィッティングしやすいので抑止するための手法が必要
そのために L1 正則化や L2 正則化といった正則化手法により、特定のニューロンに過度に依存しないようにするようにしてオーバーフィッティングを抑えり、early stopping (早期停止) でオーバーフィッティングする前に学習を止めるといったことが行われていました。
ドロップアウトではミニバッチごとに一定割合のニューロンを使わないようにすることによって、特定のニューロン(パラメータ)への依存度を減らすことでオーバーフィッティングを減らします。
もう一つの背景として、複数のモデルを構築し各モデルの予測を平均すると、多くの場合で予測精度が上がるというものです。
いわゆるアンサンブル学習ですね。
複数のモデルで予測するアンサンブル学習のような効果がある
こちらはパラメータの初期値を変えてモデルを複数のモデルを構築し、その平均を取るだけでも効果があります。
ドロップアウトもその効果を狙っています。
ミニバッチごとに毎回違うニューロンが使われないので、以下の図のように、ミニバッチごとに違うモデルが学習されていることになります。

全部で \(n\) 個のニューロンがあったとすると、各ニューロンが使う/使わないの2通りあるため、モデルは\(2^n\)個存在することになります。
ドロップアウトは、この\(2^n\)個のモデルを少しずつ学習していると考えられます。
そして、テスト・推論時にはそのモデルの平均を取る形で予測します。
これによりアンサンブル学習と同様の効果が得られるというものです。
ただし、実際に\(2^n\)個のモデルで推論し、予測結果の平均を取るというのは計算量が多すぎて現実的ではありません。
そこで、あとで詳細は説明しますが、推論時には各ウェイトにドロップアウト確率 \(p\) をかけるいう非常にシンプルな方法で平均を近似します(右図)。
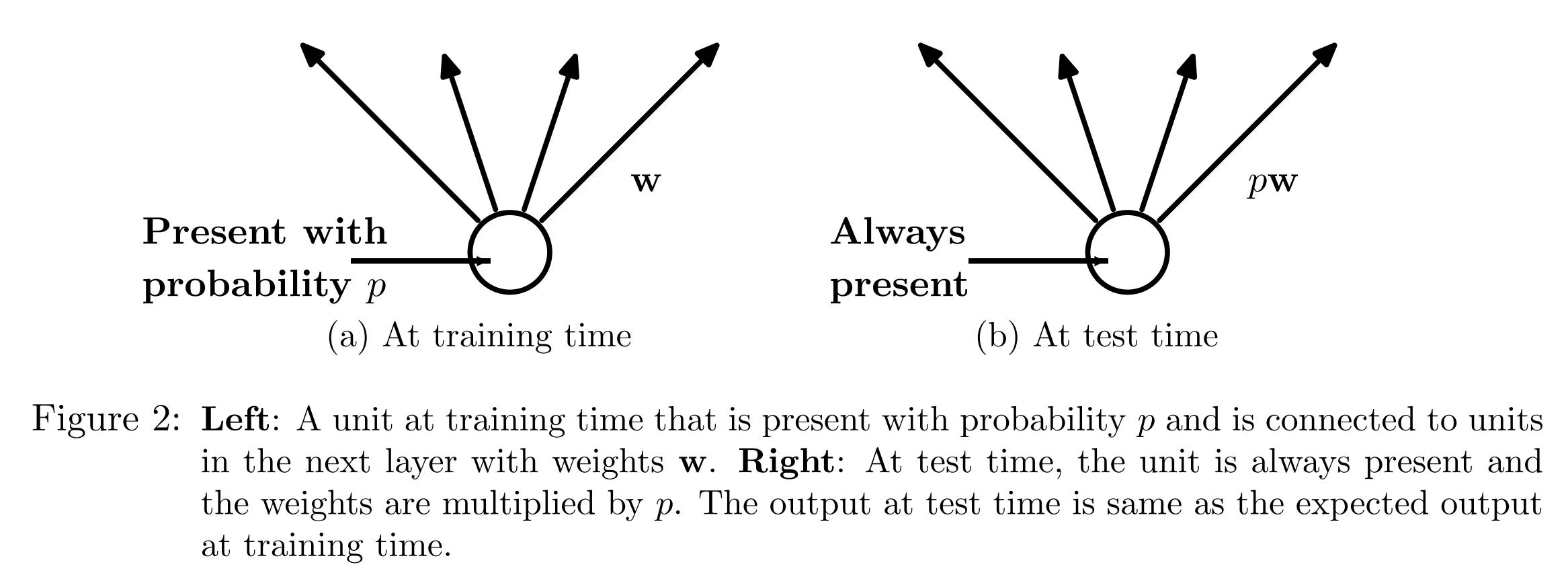
一旦、ここまでをまとめておきます。
ドロップアウトの狙い
- オーバーフィッティングを減らす
- アンサンブル効果を得る
どうやって効果を得るか
- ミニバッチごとにあらかじめ決めた確率でニューロンを使用しないようにする
どうしてその効果があるか
- 特定のニューロンを使わなくすることにより、特定のニューロンに依存しすぎなくなるためオーバーフィッティングしにくい
- 違うモデルの平均を取るのと同じなのでアンサンブル学習の効果がある
アルゴリズム
では論文で提案されているアルゴリズムを見ていきましょう。
実際にはInverted Dropoutと呼ばれる手法が実装されることが一般的ですので、あとでそちらを解説したいと思います。
学習時
学習時はドロップアウト確率\(p\)で選ばれたニューロンのウェイトを0にします。
一旦ここでは、ドロップアウト確率ではなく逆にドロップしない確率を \(q(=1-p)\) とします( keep_prob と表されたりします)。
そして確率が \(q\) の二項分布に従う乱数を振ります。
$$r_i^{(l)} \sim \text{Bernoulli}(q)$$
\(l\) は \(l\) 番目のレイヤを表し、\(i\) は \(i\) 番目のニューロンであることを表します。
\(r_i^{(l)}\) は0か1を取っています。
この \(r_i^{(l)}\) をベクトルにしたものを\({\bf{r}}^{(l)}\)としましょう。
これを \(l\) 番目のレイヤのインプットベクトル\({\bf{y}}^{(l)}\)に掛けます。
$$\widetilde{\bf{y}}^{(l)}={\bf{r}}^{(l)}*{\bf{y}}^{(l)}$$
\(*\) は要素ごとの積を表しています。
これにより選ばれたニューロンのウェイトはゼロとして使われないようになります。
そして、全結合を行い、活性化関数 \(f(\cdot)\) を通します。
$$\begin{align}
z_i^{(l+1)}&={\bf{w}}_i^{(l+1)}\widetilde{\bf{y}}^{l+1}+b_i^{(l+1)} \\
y_i^{(l+1)}&=f\left(z_i^{(l+1)}\right)
\end{align}$$
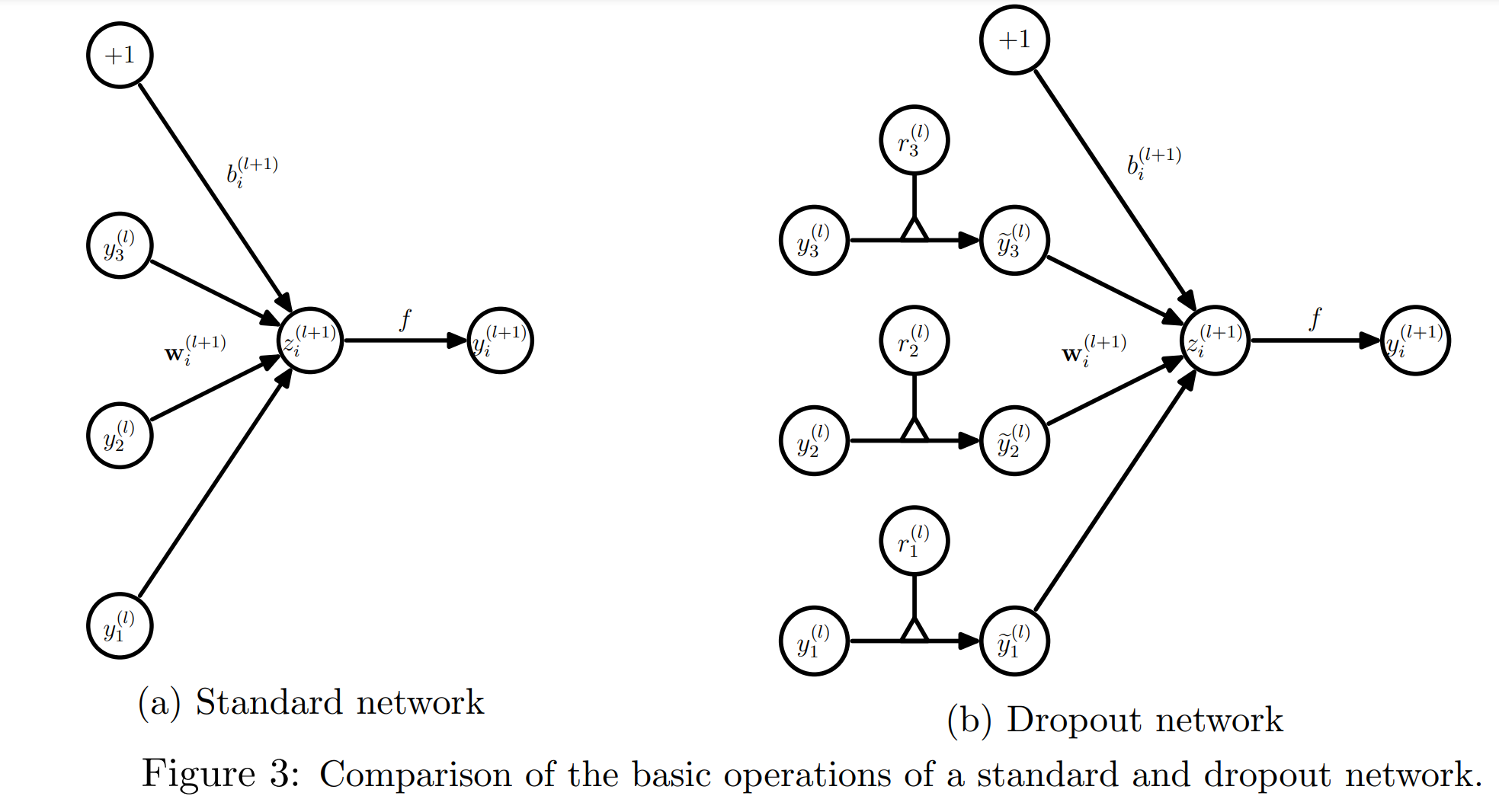
学習時は以上です。
非常にシンプルですね。
推論時
ここまででモデルの学習を行いました。
では推論時を考えていきます。
確率 \(p\) でドロップアウトして学習していたので、推論時も同じ確率 \(p\) でドロップアウトをすると学習時と整合的です。
ただしそうしてしまうと、どのニューロンをドロップアウトするかによって推論結果が変わってしまいます。
推論時はインプットが決まればアウトプットは確定的に (毎回同じ結果が) 出ないといけません。
そこで、推論時はドロップアウトせずにすべてのニューロンを使います。
推論時は毎回同じ結果になるようにドロップアウトはしない
しかしながら、そうしてしまうと良くない問題が発生します。
例えば、あるレイヤでは100個のニューロンがあり、学習時は \(p=70\)%、つまり70%をドロップアウトしていたとしましょう。
その場合、残った30%である30個のニューロンの線形結合でアウトプットを計算し、学習していました。
しかし、推論時に100%を使うとアウトプットが100% / 30%だけ大きくなってしまいます。
今までは30人で戦っていたのに、急に100人が力を合わせて戦い出したので、力が強すぎるというイメージでしょうか。
そこで、ドロップアウトを使った場合、推論時には各ニューロンのウェイトに30%、つまり \(q=1-p\) を掛けてやります。
$$W_{test}^{(l)}=qW^{(l)}$$
使うニューロンが \(1/q\) に増える代わりに各ニューロンのウェイトを \(q\) 倍してやりることで、トータルでは \(1/q\times q=1\) で、学習時と近い状態になるというものです。
推論時だけすべてのニューロンを使っていまうと、出力される値が大きくなりすぎるので (1 - ドロップアウト確率 ) を掛けることでアウトプットを調整する。
Inverted Dropout
以上が論文で使われているアルゴリズムですが、実際には Inverted Dropout というものが使われることが多く、Tensorflow や PyTorch の実装も Inverted Dropout が使われています。
背景としては、前述の通り推論時に各ウェイトを \(q\) 倍していましたが、これはネットワークを学習したときのドロップアウト確率 \(p\) もしくは保持確率 \(q\) をネットワークの情報として保存していないといけないということです。
まぁ、それでもよいのですが、Inverted Dropout では \(p\) を気にしなくても、他の人が使うことができるのでより便利です。
Inverted Dropout も単純で、学習時に
$$\widetilde{\bf{y}}^{(l)}={\bf{r}}^{(l)}*{\bf{y}}^{(l)}$$
としていたところを、さらにこの \(\widetilde{\bf{y}}^{(l)}\) を \(1/q\) 倍してやります。
$$\widehat{\bf{y}}^{(l)} = \widetilde{\bf{y}}^{(l)} / q$$
イメージとしては、先ほど“推論時に全部のニューロンを使うとアウトプットが \(1/q\) 倍 (p=0.5なら2倍) されてしまう、そのためウェイトを \(q\) 倍 (0.5倍) して推論する”と言いましたが、それに対応するためにそもそも学習時にもアウトプットを \(1/q\) 倍 (2倍) して学習してしまえ、というイメージです。
“\(\widetilde{\bf{y}}^{(l)}\) の期待値を変えない”という、よりしっかりとした説明もありますが、感覚的に言うと上記の通りです。
これにより推論時にウェイトを \(q\) 倍する必要がなく、単純にドロップアウトをせずにすべてのニューロンを使って普通に推論することができます。
ですので、Tensorflow や PyTorch のドロップアウトでは、学習フェーズかどうか?を表す引数が与えられています。
Inverted Dropout
推論時にアウトプットを \(q\) 倍するのではなく、学習時に \(1 / q\) 倍して学習し、推論時はそのまますべてのニューロンを使う
実験
ここではさらっとドロップアウトの効果を見てみましょう。
以下は手書き数字の分類データセットであるMNISTの結果です。
一番上のStandard Neural Netをベースにドロップアウトやその他の手法を組み合わせています。
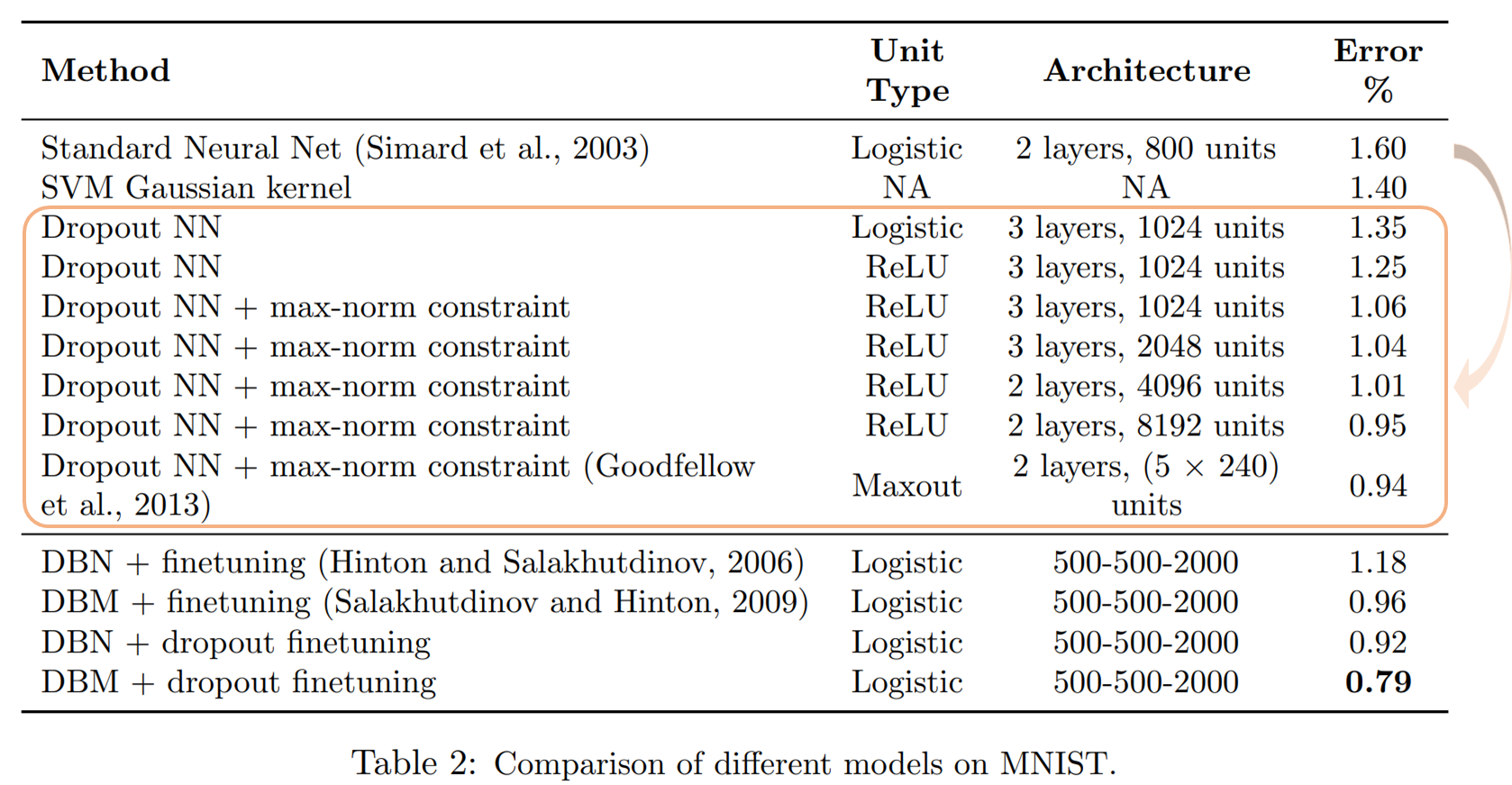
まず、ベースのエラー率が1.6%なのに対し、単純にドロップアウトを加えるだけで1.35%と0.25%も改善しています。それに活性化関数にReLUを使ったり正則化を行うことでさらに精度が改善していることがわかります。
次にいくつかのネットワークアーキテクチャでドロップアウトをした場合としない場合における学習の精度を見ていきます。
以下の図のようにドロップアウトなしの場合よりも大きく、しかも速く精度が改善していることがわかります。
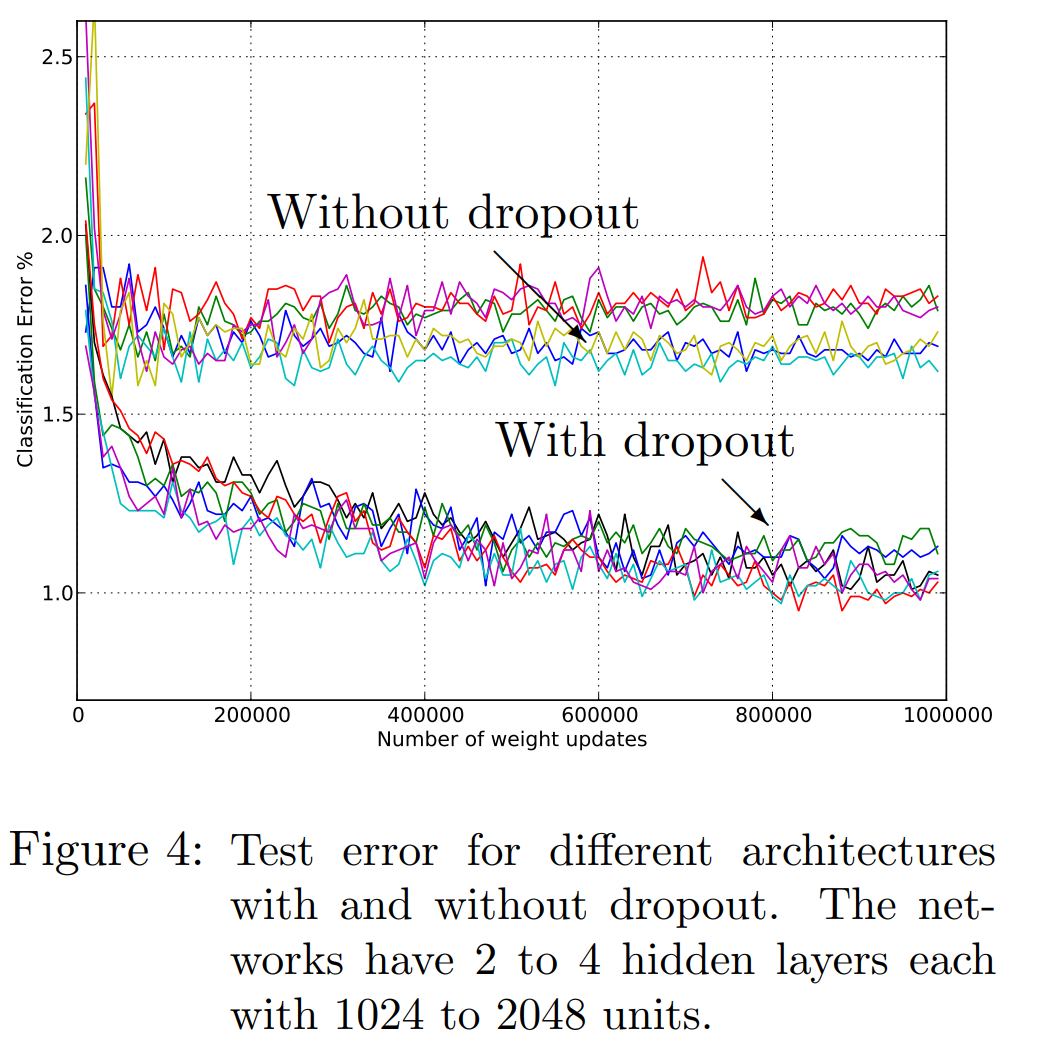
他にも実験結果はありますので、ご興味のある方は論文を参照していただければと思います。
まとめ
今回はディープラーニングでは非常に一般的になっているドロップアウトを見てきました。
バッチ正規化と同様に非常にシンプルな方法でモデルの汎化効果が非常に高く、このような手法の開発によりディープラーニングが発展してきているということですね。
勉強したての人にはしっかり理解していただき、既に知っている人にはよい復習になればと思います。
ではまた!