では、今回は2018年の重要論文の一つである“ELMo”の解説をしたいと思います。
ELMoの論文のタイトルは、“Deep contextualized word representations”であり、つまり、文脈に応じたDeepな単語表現をするものになります。
それまでのWord2VecやGloVeといった手法による単語の埋め込み表現は、一つの単語に一つの意味しか持たせられませんでしたが、ELMoではDeepなネットワークで学習することにより、文脈に応じた単語の意味を表すことが可能になります。
Word2Vecについては、こちらをご参照ください。
ELMoもOpenAI GPTやBERTと同様に、大規模コーパスを使って言語モデルを事前学習するという転移学習の考え方を使っています。
GPTやBERTでは同じ構造のモデルを使って、パラメータの初期値に事前学習済みのパラメータを設定しファインチューニングを行いますが(fine-tuning-based transfer)、ELMoは事前学習したモデルでターゲットとなる文章を読み込ませ、その隠れ層の値をターゲットとなるタスクのモデルに渡すことで(feature-based transfer)評価を改善させるものです。
転移学習の方法は違いますが、いずれにしても大規模データセットで事前学習することの重要性を示しているとも言えます。
1つのモデルで評価できるGPTやBERTの出現により、それら方が主流になっている感じがしますが、ELMoの考え方も非常に重要ですので、じっくり見ていきたいと思います。
論文はこちらです。
https://arxiv.org/abs/1802.05365
では、詳細は以下で見ていきましょう。
目次
ELMoとは
上述の通り、ELMoはDeep contextualized word representationということで、文脈に応じたDeepな単語の埋め込み表現を求めます。
今までの単語の埋め込み表現というと、Word2VecやGloVeなどが有名ですが、これらは単語を1つの低次元のベクトルで表現していました。
例えば、Word2Vecでは、以下のように周りの単語から真ん中の単語の予測を習することにより、単語の意味を表す埋め込み表現を獲得しました。
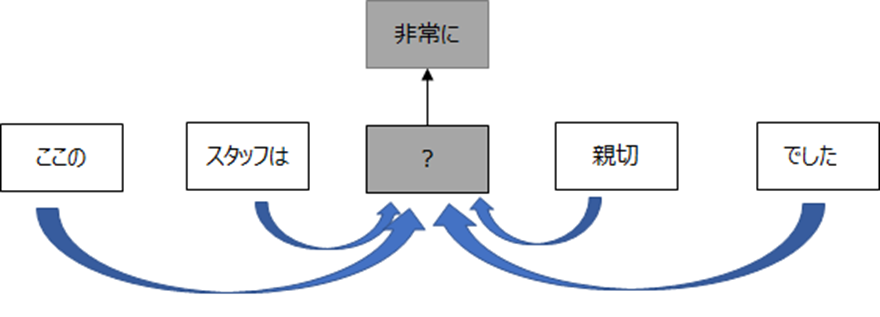
具体的には周りの単語に\(W_{in}\)というウェイトを掛けて、間の単語を予測するように学習し、その\(W_{in}\)が単語の意味を表します。
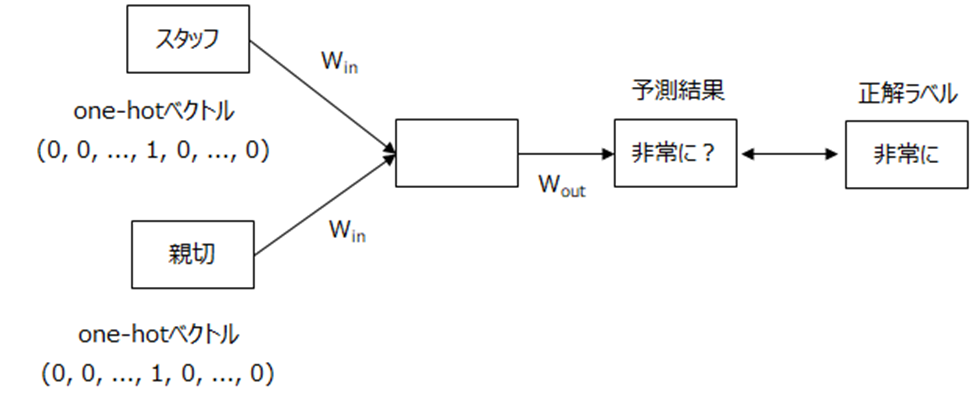
したがって、文脈は関係なく、1つの単語は1つのベクトルで表現されます。
この方法の問題点は、例えば、同じ“読む”という単語でも“本を読む”と“先を読む”のように同じ単語でも違う意味を表すことが一般的ですが、それぞれに対して表現できないことです。
ELMo(Embeddings from Language Models)ではそれを“文脈によって違う表現”を与えることを可能にします。
どうするかというと、例えばWord2Vecは周辺に出現する単語の傾向から対象となる単語の埋め込み表現を求めていましたが、ELMoでは、文章全体がインプットとなり、その文章によって単語の意味、つまり埋め込み表現が変わってきます。
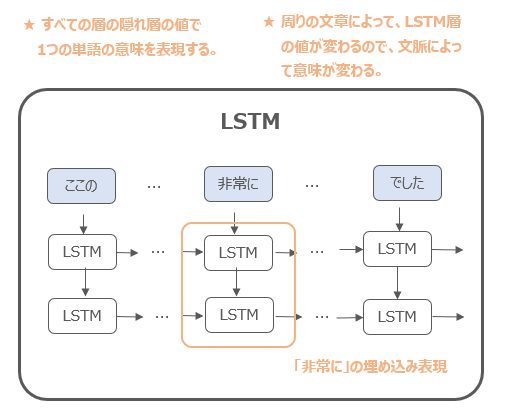
“Deepな”とは、Word2VecやGloVeでは一層のEmbeddingレイヤーのウェイトが埋め込み表現になっていましたが、ELMoではLSTMを用い、埋め込み表現がそのすべての隠れ層の出力値の関数になっています。
そういうことでDeep contextualized word representationと呼ばれています。
この埋め込み表現を後続のタスクに応じた評価で用いることになります。
ELMoの仕組み
ELMoの仕組み自体はTransformerのように特別新しい仕組みを使うわけではなく、2層のLSTMをベースとしたモデルを使います。
BERTの論文の図を拝借すると、ELMoは以下のようなモデルです。
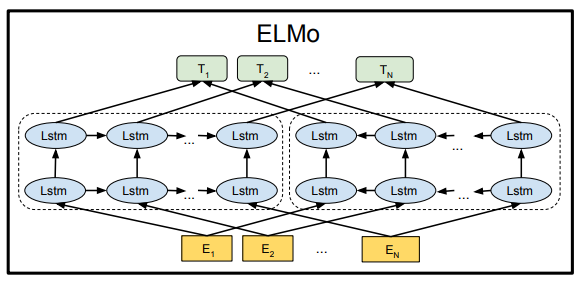
Language Understanding」
そして、そのLSTMモデルを大規模コーパスで言語モデルの事前学習を行います。
つまり、forwardを
$$p(t_1, t_2, \cdots, t_N) = \prod^N_{k=1}p\left(t_k| t_{1}, t_{2}, \cdots, t_{k-1}\right)$$
として、backwardを
$$p(t_1, t_2, \cdots, t_N) = \prod^N_{k=1}p\left(t_k| t_{k+1}, t_{k+2}, \cdots, t_N\right)$$
として学習します。
forward LM(Language Model)の\(j\)番目のレイヤーの\(t_k\)時点の隠れ層を\(\overrightarrow{\bf{h}}_{k,j}^{LM}\)とし、同様にbackward LMの\(j\)番目のレイヤーの\(t_k\)時点の隠れ層を\(\overleftarrow{\bf{h}}_{k,j}^{LM}\) とします。
そして、この言語モデルの対数尤度を以下のように、fowardとbackwardの和として計算します(これがBERTの論文では浅い双方向と言われる部分です)。
$$\begin{align}
\mathcal{L} &=\sum^N_{k=1}\left[\log p\left(t_k|t_1,\cdots,t_{k-1};\Theta_x, \overrightarrow{\Theta}_{LSTM}, \Theta_s\right) \\
+\log p\left(t_k|t_{k+1},\cdots,t_{N};\Theta_x, \overleftarrow{\Theta}_{LSTM}, \Theta_s\right) \right]
\end{align}$$
ちなみに、文章を前から読むのと、後ろから読むアウトプットを各層で結合(もしくは平均)していくような、いわゆる双方向LSTMとは違い、あくまで前から読むモデル、後ろから読むモデルでアウトプットし、その損失の合計を目的変数としています(双方向LSTMにするとあとの単語をカンニングしてしまいますので)。
ここで、\(\Theta_x\)は単語の埋め込み表現(つまりEmbeddingレイヤーのパラメータ)、\(\Theta_s\)は最終層であるsoftmaxレイヤーのパラメータ、\(\overrightarrow{\Theta}_{LSTM}\)、\(\overleftarrow{\Theta}_{LSTM}\)がそれぞれfoward LM、backward LMのLSTMレイヤーのパラメータを表します。
ELMo
ここまでは普通の双方向言語モデルの話でした。
ここからがELMo特有の話になります。
ELMoは、双方向言語モデルの中間層による単語の表現です。
つまり、またBERTの図を拝借すると、以下の各単語に対応するLSTMの隠れ層の値やEmbedding層の値の平均を取ったり、重みづけしたりして、得られるベクトルが、その単語のDeepな埋め込み表現となります。
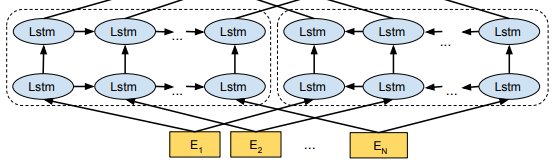
Language Understanding」
では、少し詳しく見ていきましょう。
まず、Embedding層、中間層の値を
$$\begin{align}
R_k&=\left\{{\bf{x}}_k^{LM}, \overrightarrow{\bf{h}}_{k,j}^{LM}, \overleftarrow{\bf{h}}_{k,j}^{LM} |j=1,\cdots, L \right\}\\
&=\left\{{\bf{h}}_{k,j}^{LM} |j=1,\cdots, L \right\}
\end{align}$$
で表します。
そして、ELMoは\(R\)を一つのベクトルにしたもので、例えば文章中の\(k\)番目の単語のELMoによる表現は、
$${\bf{ELMo}}_k=E(R_k;{\bf{\Theta}}_e)$$
と表されます。
この\(E\)の取り方は色々ありますが、例えば1番最後のレイヤーのみを利用する場合、
$${\bf{ELMo}}_k={\bf{h}}_{k,L}^{LM}$$
になります。
右下の添え字が\(L\)になっており、最後のLSTM層のアウトプットがELMoによる埋め込み表現になります。
しかしながら、一番最後のレイヤーだけを使うとDeepな表現にはなりませんので(論文中にも一番最後のレイヤーだけを使うのではなく、すべてのレイヤーを使う方が良いことが示されています)、基本的にはすべての層を使って求めます。
したがって、より一般的には、タスクによって以下のようにレイヤーの重みを変えてやることで定義できます。
$${\bf{ELMo}}_k^{task}=E(R_k;\Theta^{task})=\gamma^{task}\sum^L_{j=0}s_j^{task}{\bf{h}}_{k,j}^{LM}$$
\(s_j^{task}\)は重みづけを変えるパラメータ、\(\gamma^{task}\)はスケールパラメータです。
そして、特定のレイヤーのウェイトが極端に大きくならないように\(\lambda||{\bf{w}}||^2_2\)を損失関数に加えることでL2正則化を行います。
\(\lambda\)は正則化のためのパラメータです。
ELMoを使った教師あり学習
さて、このELMoを教師あり学習に対してどのように使うのでしょうか。
それには、まず、上述の事前学習済み双方向言語モデルを使って対象となる文章を読み込ませ、ELMo(つまり各単語のDeepな埋め込み表現)を計算します。
そして、そのELMoをEmbeddingレイヤーに追加して、\(\left[{\bf{x}}_k; {\bf{ELMo}}_k^{task}\right]\)として結合します。
そして、そのまま教師あり学習を進めます。
この場合、事前学習を行った言語モデルと同じである必要はないので、それぞれタスクにあったモデルを使います。
このように他で事前学習した情報を、説明変数に追加する、つまり特徴量として転移する方法をfeature-based transferと言います。
一方で、BERTやGPTなどは、事前学習も教師あり学習も同じ構造のモデルを使い、モデルのパラメータの初期値として事前学習したパラメータを設定し、それを調整することから、fine-tuning-based transferと呼ばれます。
どちらかというと現在はfine-tuning-based transferの方が主流になっているように思えますが、その一因として、feature-based transferでは、ELMoのように事前学習した特徴量を対象となるタスクに追加しますが、改めて対象となるタスクのモデルを一から時間をかけて(教師あり)学習しないといけないということがあります。
一方のfine-tuning-based transferでは、初期値に事前学習で得た良いパラメータを設定するため、数エポックで収束するというメリットがあり、事前学習は時間をかけて済ましておき、各タスクの学習はさくっと終わるということです。
事前学習モデル
では、ELMoを計算するための双方向言語モデルの詳細について見ていきます。
基本的には、LSTMですが、各LSTMレイヤーには残差結合を使っています。
また、これはELMoの本質的なところではないため、詳しい説明は省略しますが、モデルは単純な双方向LSTMではありません。
LSTMレイヤーに入力する前に、単語をそのまま埋め込み表現に変換するのではなく、文字ベースの埋め込み表現に変換します。
そして、その文字ベースの埋め込み表現をConvolutionalレイヤー、max-poolingレイヤーで処理し、さらに2層のハイウェイ・ネットワークを通します。
詳細はこちらの論文をご参照ください。
このモデルを使って、1B Word Benchmarkコーパスという文章をたくさん集めたデータセットで学習します。
ターゲット・タスクのドメインのデータを使って追加で学習させると、さらにパープレキシティが減少し、後続のタスクが改善することがAppendixで確認されています。
やはり同じドメインで学習させた方が良くなりそうですね。
実験
では、いくつかのタスクを学習した結果を見てみましょう。その他もELMoを加えることにより精度が改善していることは一目瞭然です。
Question Answering
まずはSQuADデータセットです。
この教師あり学習にはBidirectional Attentino Flowモデルというものを使っています。
繰り返しになりますが、ELMo自体はモデルの構造を意味するわけではないので、事前学習とは違うそのタスクに合ったモデルを使います。
そして、そのモデルにELMoを追加し学習した結果が以下になります。
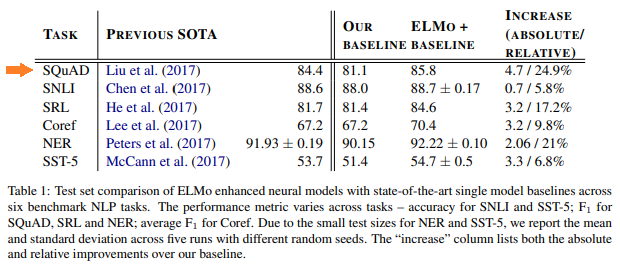
もともとのモデルのF1スコアは84.4%だったのですが、この論文での81.1%になっています。
そして、そのモデルにELMoを加えることにより85.8%と4.7%上昇し、相対的には24.9%改善しています。
そして、もとのSoTAも超えています。
Sentiment Analysis
Stanford Sentiment Treebankデータセットの結果です。
こちらもELMoを追加することにより、51.4%から54.7%に改善していることがわかります(シードを変えて5回学習し、テストデータに対する平均が54.7%で、±0.5は標準偏差を表しています)。
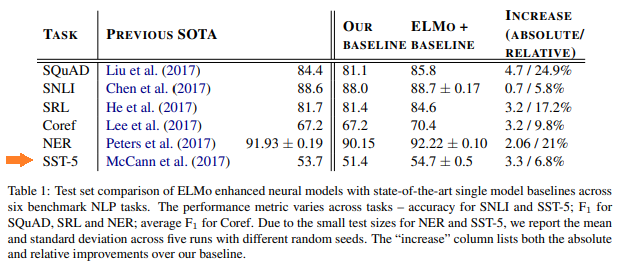
追加分析
“Deepな文脈に沿った”埋め込み表現の効果
過去の手法では、文脈に沿った埋め込み表現は、大体一番最後のレイヤーの埋め込み表現を使っていました。
ELMoでは中間層も使うことでDeepな埋め込み表現を使います。
その効果を調べるために、正則化パラメータ\(\lambda\)の影響を見ていきましょう。
正則化パラメータ\(\lambda\)が大きいほど、各レイヤーのパラメータの大きさのばらつきが抑えられます。
\(\lambda=1\)というような大きい値の場合、すべてのレイヤーで同じようなパラメータの値を取り、\(\lambda=0.001\)のような小さい値の場合、パラメータはレイヤーによって大きく変わります。
そこで、ELMoを入れない場合、最後のレイヤーだけをELMoに使う場合、すべてのレイヤーを使いますが\(\lambda=1\)とした場合と、\(\lambda=0.001\)とした場合の比較を行っています。
以下がその結果です。
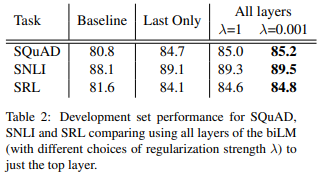
まず、ELMoを加えない場合よりも、最後のレイヤーだけを使ったELMoを追加した方が精度は大幅に向上しています。さらにすべてのレイヤーを使った方が改善していますが、\(\lambda=1\)の場合よりも\(\lambda=0.001\)の場合、つまり各レイヤーのばらつきをあまり押さえない場合の方が精度が改善していることがわかります。
これは、Deepな埋め込み表現を使う方が上記のデータセットには有効であるということ、また、各層の特徴を活かした方が精度が良くなることが示唆されているということになります。
双方向言語モデルによりどのような情報を捉えているか
これはBERTの研究などでも良く見られますが、ELMoによる言語モデルの事前学習により、単語のどんな情報を得捉えているのかを分析していきます。
個人的には非常に面白いと思ったところです。
ここでの例は、“play”という単語を例に分析しています。
下の図の上段では、まずGloVeによる埋め込み表現について、“play”に近い単語を計算しています。
“game”や“football”、“played”などといった単語が並んでいます。
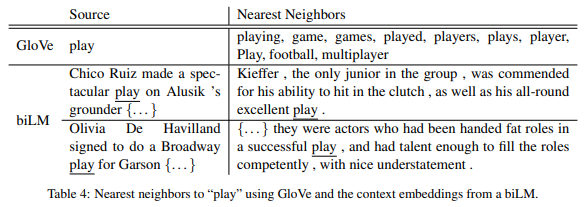
一方で、ELMoによる双方向言語モデル(biLM)では文脈によって単語の埋め込み表現が違ってくるので、ある文章に出てくる“play”と他の文章に出てくる“play”の埋め込み表現が似ている文章を抽出しています。
上図の下段ですが、そのうちの上のsource sentenceの“play”はスポーツに関する“play”なので、それに近い“play”は右側のスポーツに関する“play”が選ばれています。
一方で、下のsource sentenceの“play”は公演するの“play”なので、それに近い文章は公演するを意味する“play”が選ばれています。
語義の曖昧性解消(Word Sense Disambiguation; WSD)
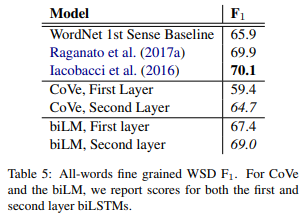
ここでは、語義の曖昧性解消(Word Sense Disambiguation; WSD)というタスクを解きます。
これは、ある文章の単語が複数の意味を持つ場合に、どの単語が一番近い意味を持つ単語かを予測します。
それを双方向言語モデルの1つ目のレイヤーの埋め込み表現を使った場合と2つ目のレイヤーの埋め込み表現を使った場合で比較します。
結果は以下の通りで、2つ目のレイヤーを使った方がF1スコアが1.6%改善しています。
論文には書かれていませんが、2つ目のレイヤーの方が文脈に沿った意味を捉えているかなと考えられます。
品詞タグ付け(POS tagging)
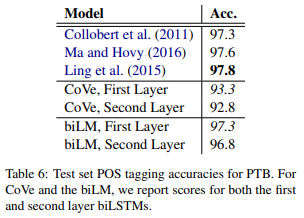
次に品詞タグ付けのタスクを解いてみます。
同じように1つ目のレイヤーに分類用のレイヤーを加えて分類する場合、2つ目のレイヤーに分類用のレイヤーを加えて分類する場合で比較します。
今回は2つ目のレイヤーよりも1つ目のレイヤーを使った方が精度が若干改善しています。
結論
以上の結果より、双方向言語モデルにより文脈に沿った単語の意味が捉えられていること、1つ目のレイヤーと2つ目のレイヤーはそれぞれ違う情報を捉えていることが示されています。
特に後者の理由により、ELMoとして一番最後のレイヤーの情報だけを使うより、すべてのレイヤーの情報を使った方が後続タスクの精度改善に寄与すると考えられます。
まとめ
今回は2018年の重要論文の一つELMoを見てきました。
Word2VecやGloVeなどでは捉えられなかった文脈に沿った埋め込み表現というものをELMoでは獲得するという決定的な進歩がありました。
本文中にももう少し分析がありますが今回は割愛しています。
また、Appendixには他にも細かい分析があり、それはそれで面白い内容になっていますので、興味がある方は直接論文を参照いただければと思います。
