今回はモデルというよりも、モデルの中で使われている一つの仕組み、“Layer Normalization”について解説したいと思います。
Layer Normalizationはディープラーニングの基礎的な本では、ほぼ必ずと言っていいほど登場する“Batch Normalization”を改良したもので、TransformerやBERTでも使われています。
Batch Normalizationについてはこちらの記事『Batch Normalizationを理解する』をご参照ください。
この仕組みを深く知らなくてもBERTなどの理解はできますが、やはり細かい技術なども論文を読んでしっかりと理解した方が良いと思いますので、以下の論文をベースに説明していきたいと思います。
https://arxiv.org/abs/1607.06450
TransformerやBERTに関してはこちらをご参照ください。
Transformerの解説
BERTの解説
Batch Normalizationとは
ではまず、Batch Normalizationについて簡単に説明したいと思います(詳しくはこちら『Batch Normalizationを理解する』)。
Batch Normalizationは2015年に“Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”というで最初に提案された仕組みになります。
https://arxiv.org/abs/1502.03167
タイトルにある通り、“Internal Covariate Shift”を減らして学習を加速するということですが、この“Internal Covariate Shift”というのは、内部の共変量がシフトする、つまり各レイヤーへのインプットとなる変数の分布が変わってしまうことを意味します。
もとのインプットである\({\bf{x}}\)や\(l\)番目の中間層のアウトプットである\({\bf{a}}^l\)の分布がパラメータを調整する過程でバッチごとに変わってしまうというのが“Internal Covariate Shift”です。
なぜそれが問題かというと、例えば活性化関数がSigmoid関数の場合を考えてみます。
Sigmoid関数は絶対値の大きなインプットに対しては、傾きはほぼゼロになってしまいます。
ですので、学習過程でウェイト・パラメータが大きな値を取ると次のレイヤーの勾配が非常に小さくなり学習が進みません。
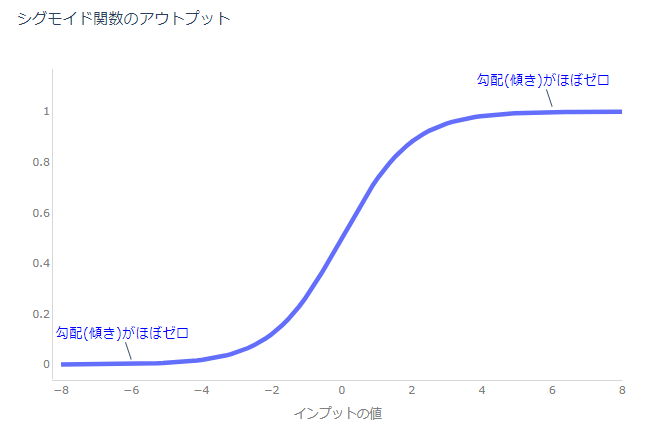
活性化関数にReLUなどを使えば回避可能ではありますが、こういった分布の変化を抑え、例えば一定数のサンプルを中心部分に近づけるような処理を入れることで学習を加速させよう、というのがBatch Normalizationになります。
Batch Normalizationのアルゴリズムは論文を引用すると、以下の通りになります。

各レイヤーへのインプット\(x\)について、ミニバッチごとに平均、分散を求め、インプットを正規化します。最後に、\(\beta\)、\(\gamma\)というパラメータ(学習する)によりもう一度平均と分散をシフトします。
これは\(\beta=0\)、\(\gamma=1\)であれば正規化したものと変わらないですし、仮により良くなるようであれば平均・分散をシフトさせるというイメージです。詳細は論文をご参照ください。
続きのLayer Normalizationとの比較のために、Layer Normalizationの論文の説明も追加しておきます。
\(l\)番目のレイヤーの\(i\)番目のニューロンの出力値\(h_i^{l+1}\)は活性化関数\(f\)を使って
$$\begin{align}
a_i^l &= {w_i^l}^Th^l\\
h_i^{l+1}&=f\left(a_i^l+b_i^l\right)
\end{align}$$
で計算します。そして、平均・分散を
$$\begin{align}
\mu_i^l&=\mathbb{E}_{{\bf{x}}~P({\bf{x}})}\left[a^l_i\right]\\
\sigma_i^l&=\sqrt{\mathbb{E}_{{\bf{x}}~P({\bf{x}})}\left[\left(a^l_i-\mu_i^l\right)^2\right]}
\end{align}$$
で計算しますが、Batch Normalizationでは、データ全体の平均・分散ではなく、ミニバッチごとの平均・分散を計算します。
そして、
$$\bar{a}_i^l=\frac{g^l_i}{\sigma^l_i}\left(a^l_i-\mu^l_i\right)$$
で、出力値を計算します。\(g_i^l\)はスケーリング・パラメータです。
これをsigmoid関数などの活性化関数のインプットとします。
Layer Normalization
では、本題のLayer Normalizationを見ていきましょう。
Batch Normalizationはシンプルで非常に効果的な方法ですが、以下の問題点が指摘されています。
- データセット全体の平均・分散ではなく、ミニバッチごとに平均・分散を計算するため、ミニ・バッチが小さい場合、平均・分散が不安定になる
- 再帰的ニューラルネットワークに適用するのが難しい
一つ目は、メモリの関係などでミニバッチサイズを小さくすることがよくありますが、その場合、ミニバッチごとに平均・分散を計算すると推定値が不安定になってしまうということです。
二つ目は、再帰的ニューラルネットワークでは、各サンプルごとに文章の長さが違い、学習データよりも長い文章がテストデータにある場合、適用が簡単ではないということです。
そこで、Layer Normalizationでは、1つのサンプルにおける各レイヤーの隠れ層の値の平均・分散で正規化します。
$$\begin{align}
\mu^l&=\frac{1}{H}\sum^H_{i=1}a_i^l\\
\sigma^l&=\sqrt{\frac{1}{H}\sum^H_{i=1}\left(a_i^l-\mu^l\right)^2}
\end{align}$$
Batch NormalizationとLayer Normalizationの違いを図にすると以下のようになります。
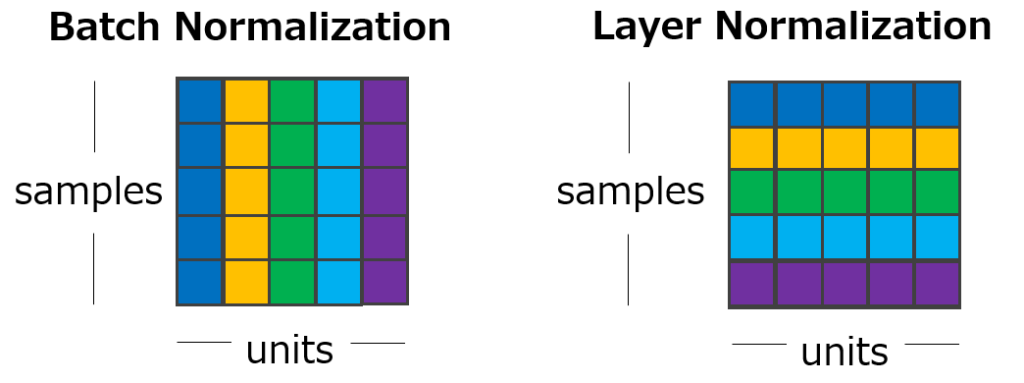
これにより、ミニバッチのサイズが小さくても、サンプルが1つでも問題なくなります。
では、これを再帰的ニューラルネットワークに適用するにはどうすればよいでしょうか。
それを次で見ていきたいと思います。
Layer Normalized Recurrent Neural Networks
RNNでは、時系列に各時点の活性化関数の値が流れていきます。
シンプルなRNNは以下のように表されます。\(t\)は時点を表しています。
$$\begin{align}
a_i^{t+1} &= {w_i}^T h + {w_i^x}^T, \\
h_i^{t+1} &= f(a_i^{t+1} + b_i)
\end{align}$$
このRNNにBatch Normalizationを単純に適用しようとすると、まず各時点におけるミニバッチごとの平均・分散を計算し、それらを使って正規化することが考えられます。
$$\bar{a}_i^{t+1}=\frac{g_i}{\sigma^{t}_i}\left(a^{t}_i-\mu^{t}_i\right)$$
ただ、自然言語処理などでは、インプットである文章の長さは一定ではありません。
ですので、テストサンプルに学習サンプルよりも長い文章が合った場合、正規化するための平均・分散がないという問題があります。
Layer Normalizationであれば、RNNへの適用は簡単です。
各時点\(t\)における隠れ層の値を使って平均・分散を求めます。
$$\begin{align}
\mu^{t}&=\frac{1}{H}\sum^H{i=1} a_i^{t},\\
\sigma^{t}&=\sqrt{\frac{1}{H}\sum^H_{i=1}\left(a_i^{t} -\mu ^{t} \right)^2}
\end{align}$$
そして、それらを使って正規化し、スケーリングしたうえで、活性化関数を適用します。
$${\bf{h}}^t = f\left[\frac{{\bf{g}}}{\sigma^{t}}\odot \left({\bf{a}}^{t}-\mu^{t}\right)+{\bf{b}}\right]$$
ですので、RNNなど可変長のデータに対するモデルではLayer Normalizationを使う方が簡単です。
実験
では、実験結果を見てみましょう。
まずは、attentive reader modelというモデルを使って、Question-answeringタスクを解いた場合について、
- Batch Normalizationをすべてのレイヤーで使った場合(BN-everywhere)
- Batch NormalizationをLSTMレイヤーだけに使った場合(BN-LSTM)
- Layer NormalizationをLSTMレイヤーに使った場合(LN-LSTM)
- いずれも使わない場合(LSTM)
で比較しています。
一目瞭然ですが、LN-LSTMが一番収束が早く、精度も一番良くなっています。
何も使わない場合との収束スピードはまったく違いますね。
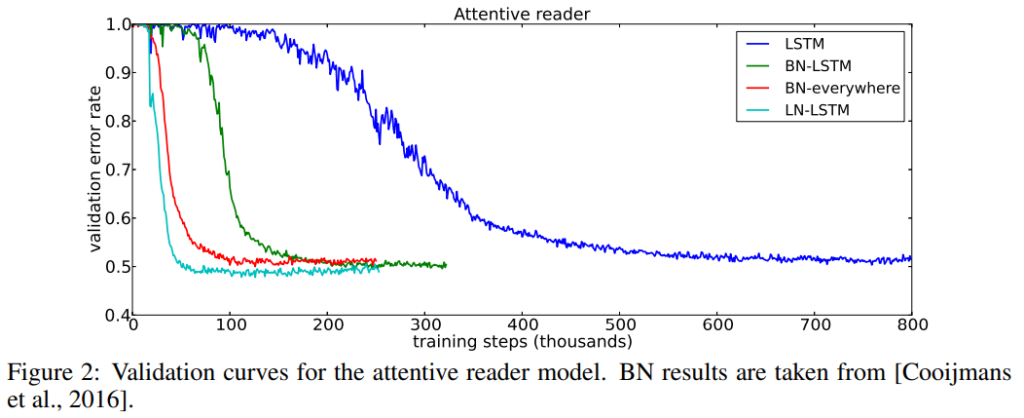
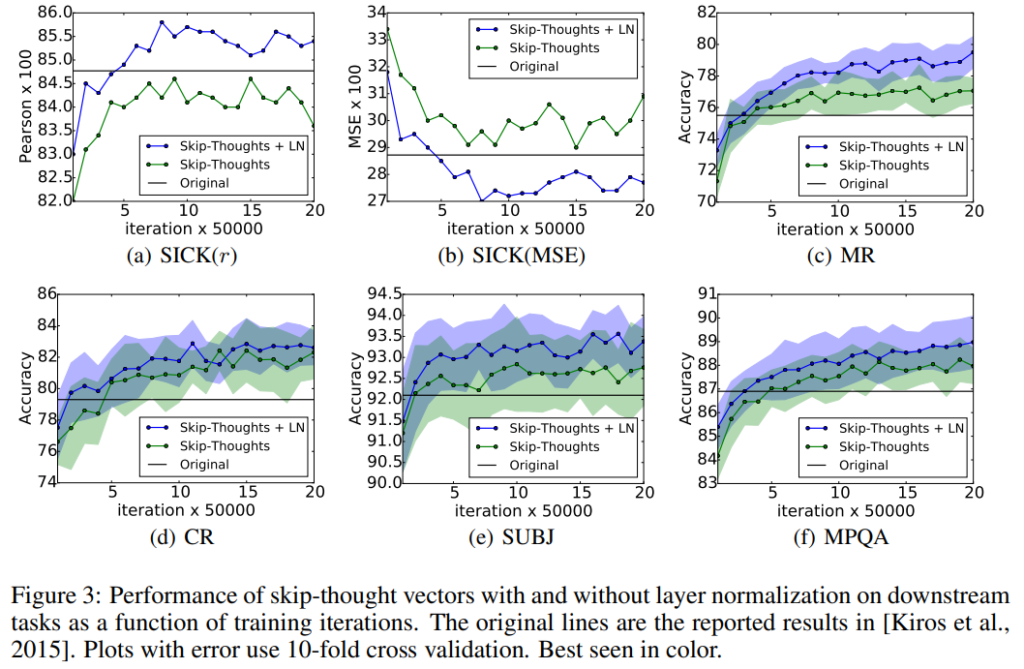
次にSkip-thought vectorsを使っていくつかのタスクを解いた場合です。
Layer Normalizationを使った方が収束が早く、精度も良いことがわかります。
まとめ
今回は、TransformerやBERTなど色々なところで使われているLayer Normalizationについて、手法を確認しました。
非常にシンプルな方法ですね。
今回は、詳しい分析についての説明は省略していますので、ご興味がある方は論文を読んでいただければと思います。
正規化手法には他にも主に画像分野で使われているGroup NormalizationやInstance Normalizationといった手法もあります。
こちらも興味がある方は解説記事や論文を参照していただければと思います。
では!



