今回はTransformerの改良版であるReformerを解説したいと思います。
BERTもそうですが、Transformerで長文を処理しようとすると、非常にメモリ使用量が多く、2000単語ぐらいでも非常に遅くなります。
ReformerはTransformerのScaled Dot-Product Attentionの仕組みを改良することで、大幅にメモリ使用量を削減し、6万4000単語という非常に長い文章も取り扱えるようになったモデルです。
そしてこのReformerにより、数行単位の文章ではなくWikipediaの記事レベルの大きさの文書までを生成することが可能になりました。
原論文はこちらです。
https://arxiv.org/abs/2001.04451
では、さっそく見ていきたいと思います。
目次
Reformerとは
Transformerは、attentionの計算部分であるScaled Dot-Product Attentionのところで、必要なメモリ数が文章の長さの2乗に比例(\(O(L^2)\))します。数十や数百単語ぐらいであればそれほど気にならず、LSTMなどと比べて計算速度が速いため快適ですが、数千単語の文章(パラグラフ)となると非常に計算負荷が高くなります。(Scaled Dot-Product Attention、Transformerがわからない方はこちらをご参照いただければと思います)
そこで、ReformerではそのattentionをLocality-Sensitive Hashing(LSH)という手法を用いて効率化することで、メモリの必要量を\(O(L\log L)\)に抑えます。それにより、Wikipediaの記事のような大きな文書さえも生成することが可能になりました。
また、BERTやXLNetでは、例えば1,028次元の隠れ層を使い、FeedForwardレイヤーではさらにその4倍の4,096次元としていますが、バックプロパゲーションのためにそれらの活性化関数の値を保持しておく必要があります。そして、それはレイヤーの数分必要になるので非常に多くなります。そこでReversible Transformerという仕組みを導入することにより、活性化関数の値自体をバックワードで計算することができるようします。それにより、従来はレイヤーの数分必要だったメモリを1レイヤー分だけに抑えることで、必要なメモリの量を減らしています。
上記の通りReformerのポイントは以下の2点です。
- Locality-Sensitive Hashing(LSH)により使用するメモリ量を\(O(L^2)\)から\(L\log L\)にする。
- Reversible Transformerで各レイヤーごとに活性化後の値を保持する必要をなくし、メモリの使用量を減らす。
では、詳細を見ていきましょう。
Reformerの仕組み
Transformerのメモリ使用量
Transformerのメモリ上の問題点は、Scaled Dot-Product Attentionの計算部分の以下の計算です。
$$\begin{align}
Attention(Q,K,V) = \text{softmax}(QK^T/\sqrt{d})V\\
\end{align}$$
Value \(V\)を掛ける前のsoftmaxの部分が、Query \(Q\)からKey \(K\)に向ける注意の割合を計算しています。
そして、\(Q, K\in\mathbb{R}^{L\times d}\)なので、\(QK^T\in \mathbb{R}^{L\times L}\)になり、文章の長さの2乗になります。したがって、文章が長い場合64,000単語の場合、要素の数は約40億個になり、32bit float(=4byte)だと163億バイト、つまり16GBになります。バッチサイズを8にするとたった一つの変数だけで131GBにもなってしまい、計算ができません。実際には2000単語とかでかなり辛くなります。
そこで、このAttentionの計算を近似することを考えるというのがReformerです。
Memory Efficient Attention
Query \(Q\)から1つのベクトルだけ取り出す、つまり1つの単語の部分だけ取り出して見てみましょう。\(i\)番目のクエリー(単語) \(q_i \in \mathbb{R}^d\)を考えると、これが向ける注意は\(q_iK^T=(q_ik_1, q_ik_2, \cdots,q_ik_L)\in\mathbb{R}^{1\times L}\)です(厳密には\(\sqrt{d}\)で割ったり正規化したりしますが)。つまり、\(k_1\)へ注意は\(q_1 k_1\)、\(k_2\)への注意は\(q_2 k_2\)といった具合です。
ここで重要なのは、この\(q_ik_j\)が相対的に大きい場所だけであり、それ以外のところの重要度は高くありません。そして内積\(q_i k_j\)が大きいというのは\(q_i\)と\(k_j\)が似ている場合です。つまり、\(q_i\)と似ているベクトルが場所\(j\)が重要な部分になります。
そこで、\(q_i\)に似ている\(k_j\)をうまく求めて、似ているkeyだけを使って計算することを考えていきます。それが次のLocality-Sensitive Hashing(LSH)と呼ばれる手法です。
Locality-Sensitive Hashing(LSH)
Locality-Sensitive Hshing(LSH)は、最近傍探索(似たようなベクトルを探す)のためのアルゴリズムで、簡単に言うと、ベクトルをあるハッシュ・バケット(例えばハッシュ1、ハッシュ2、…)に分類するのですが、その際に似ているベクトルは同じハッシュに、似ていないベクトルは違うハッシュに分類することを言います。
どうやるかというと、非常にシンプルなRandom Rotationというものを使います。以下はベクトルが2次元の場合のイメージ図です。

下側が2つのベクトルxとyが似ている場合で、3パターンのprojectionを例示しています。Random Projection 0, 1, 2とくるくる回転させており、白、青、緑、赤の領域が4つのハッシュ・バケットです。下側の例では2つのベクトルは非常に似ていることから、くるくる回転させても、Random Projection 0は2つとも白、Random Projection 1は2つとも緑、Random Projection 2は2つとも青とすべて同じバケットに入っています。
一方で、若干離れている上の例では、Random Projection 0とRandom Projection 2の例でxとyは違うバケットに入っています。
というような感じで、ベクトルをくるくる回転させて同じハッシュ・バケットに入っていれば、同じハッシュとみなします。
では、このくるくる回転させるのはどうするかというと、Random matrixを掛けることでできます。後で具体例を見たほうがわかりやすいかもしれませんが、ざっと説明します。
まず、分けたいバケットの数を\(b\)とすると、Random matrixを\(R\in \mathbb{R}^{d_k\times b/2}\)として、 標準正規分布乱数で与えてやります。そして、random projectionを\([xR; -xR]\in \mathbb{R}^{b}\)で計算します。セミコロンは連結を意味します。そして、
$$h(x)=\arg\max\left[xR;-xR\right]$$
として、回転後の数値が一番大きい添え字をそのハッシュ・バケットとして選びます。
では、以下の3つのベクトルを4つのバケットに分ける例を見てみましょう。
x_1 = np.array([0.1, 0.2, 0.3]) x_2 = np.array([0.2, 0.3, 0.1]) x_3 = np.array([-0.1, -0.3, -0.2])
\(x_1\)と\(x_2\)、\(x_1\)と\(x_3\)のcosine similarityは、
from sklearn.metrics.pairwise import cosine_similarity print(cosine_similarity(x_1.reshape(1, -1), x_2.reshape(1, -1))) print(cosine_similarity(x_1.reshape(1, -1), x_3.reshape(1, -1)))
とすると、それぞれ0.79と-0.93となり、\(x_1\)と\(x_2\)は似ていますが、\(x_1\)と\(x_3\)は似ていません。
ここで、標準正規乱数発生させてrandom matrix \(R\)を作成します。
num_of_hash = 4 d = 3 R = np.random.randn(d, int(num_of_hash / 2))
そして、\(\arg\max=\left(\left[xR; -xR\right]\right)\)でどのハッシュにするかを計算します。例えば、\(x_1\)の場合、
x_1_r = np.dot(x_1.reshape(1, -1), R) x_1_r = np.concatenate([x_1_r, -x_1_r], axis=1) print(x_1_r)
とすると、
[-0.14220674 0.25683456 0.14220674 -0.25683456]
なので、2番目のハッシュが選ばれます。同様に、\(x_2\), \(x_3\)についても計算すると、\(x_2\)は
[-0.064634 0.35464789 0.064634 -0.35464789]
なので2番目のハッシュが、\(x_3\)は
[ 0.13898525 -0.4169439 -0.13898525 0.4169439 ]
となり、4番目のハッシュが選ばれます。
つまり、似ている\(x_1\)と\(x_2\)は同じハッシュに入り、似ていない\(x_3\)は違うハッシュに入ります。
この方法により、queryに対するkeyをハッシュ・バケットに分け、queryと同じハッシュ・バケット内だけでattentionを計算することにより、メモリ量を減らそうというものです。
LSH attention
では、具体的にLSHを使ってどのようにattentionを計算するかを論文に沿って確認していきましょう。一見、読みづらいように思えますが、言っていることは割と簡単です。
まず、普通のattentionは以下のように書けます。論文ではfull attentionと呼んでいます。
$$\begin{align}
o_i = \sum_{ j\in\mathcal{P}_i}\exp\left(q_i\cdot k_j-z(i,\mathcal{P}_i)\right)v_j
\end{align}$$
ここで、\(\mathcal{P}_i=\{j:i\ge j\}\)で、時点\(i\)より前の位置になり、自然言語処理の話で言うと\(i\)番目の単語より前の単語を表します(その単語も含みます)。つまり、自分より先の単語を見ないようにマスクされた式になっています。\(z(i,\mathcal{P}_i)\)はsoftmax関数の分母に当たる部分です。見慣れた式で書くと、
$$
\begin{align}
\text{context_vector }o_i = \sum_{ j\le i}\text{attention_weights}_j\cdot v_j,\\
\text{attention_weights}_j =\frac{\exp\left(q_i\cdot k_j\right)}{\sum_{j\le i} \exp\left(q_i\cdot k_j\right) }
\end{align}
$$
です。そして、実際の計算方法に合わせて書き換えると、
$$\begin{align}
o_i = \sum_{ j\in\widetilde{\mathcal{P}}_i}\exp\left(q_i\cdot k_j-m(j,\mathcal{P}_i)-z(i,\mathcal{P}_i)\right)v_j,\\
m(j,\mathcal{P}_i)=\left\{\begin{array}{l,l}
+\infty&\text{if } j\notin \mathcal{P}_i\\
0&\text{otherwise}
\end{array}\right.
\end{align}$$
となります。\(m(j, \mathcal{P}_i)\)というのが出てきていますが、これがマスク部分になります。ようは、\(j\notin \mathcal{P}_i\)なら\(+\infty\)なので、\(i\)番目より後の単語であれば\(m\)を無限大にしてマスクするということです。よくわからないという方は、Transformerを実装していればわかると思いますので、以下をご参照ください。
そして、\(j\in\widetilde{\mathcal{P}}_i\)に対して合計するのですが、\(\widetilde{\mathcal{P}}_i=\{0, 1\cdots, l\}\)とすべての単語を表すので、結局はすべての単語について合計しながら、\(m\)によりマスクするということです。
時間をかけてしまいましたが、ここまでは、普通のTransformerの話です。ここからReformerのLSH attentionにしていきます。まず、普通のTransformerでは、自分より前の単語すべてに注意を向けるので\(\mathcal{P}_i=\{j\le i\}\)としていましたが、LSH attentionでは同じハッシュ・バケットの単語のみに注意を向けるので、
$$\mathcal{P}_i=\{j:h(q_i)=h(k_j)\}$$
とします。つまり、query \(q_i\)と同じバケットに入るkey \(h_j\)だけがattentionを向ける先にするということです。
LSH attentionの手順
では、LSH attentionの仕組みがわかったところで、具体的なアルゴリズムを見ていきたいと思います。
以下の図の順番で処理を行いますので、こちらを一つずつ確認していきます。
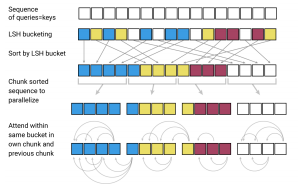
Query, Keyの共有
説明を飛ばしていましたが、まず、query = keyとします。
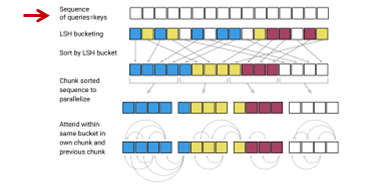
なぜかというと、keyをハッシュに分けると特定のハッシュの中にqueryはたくさんあるのに、keyがまったくない、なんてことが起こります。これを和らげる目的で、query = keyとします。具体的には、keyは正規化して
$$k_j=\frac{q_j}{||q_j||}$$
とします。こんなことしていいの?と思うかもしれませんが、これで問題ないことがあとで検証されています。
LSH
そして、上述のrandom matrixを掛ける方法によりハッシュ・バケットに分けます。
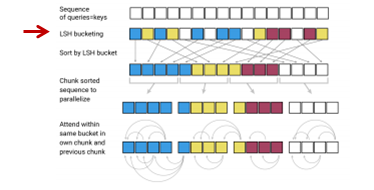
そして、ハッシュ・バケットごとに並び替えます。
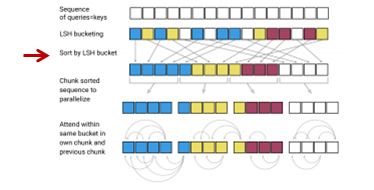
チャンク化
attentionを向ける先自体はハッシュ・バケットごとに計算しますが、ハッシュ・バケットによってはバケット内のkey(=query)の数が1個だったり10個だったりして数が違うため処理がしづらいので、連続したm個のqueryを1つのチャンク分割し、計算します。そして、後述しますが、自分がいるチャンクとその前のチャンクにある同じバケットのqueryのみattentionを計算します。
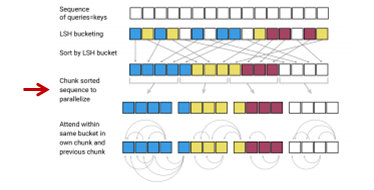
ここで1つのチャンクのサイズ\(m\)は、
$$m=\frac{2l}{n_{buckets}}$$
で決めます。\(n_{buckets}\)はバケット数(チャンク数ではなく)なので、平均的なバケットの中の単語数(バケットサイズ)の2倍を1つのチャンクにします。これは、平均的なバケット・サイズの2倍以上離れたところに同じハッシュ・バケットに入るkey(=query)はないだろうという仮定です。
LSH attention
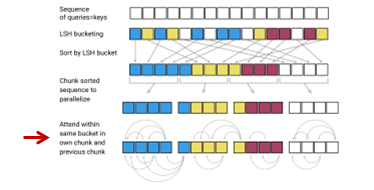
そして、query \(q_i\)からattentionを計算する対象の集合\(\widetilde{\mathcal{P}}_i\)は、チャンク単位で考えて、
$$\widetilde{\mathcal{P}}_i=\left\{j:\left\lfloor \frac{s_i}{m} \right\rfloor-1 \le \left \lfloor\frac{s_j}{m} \right \rfloor\le \left \lfloor\frac{s_i}{m} \right \rfloor\right\}$$
になります。\(s_i\)はバケットごとに並べ替えた後の添え字になります。ですので、左側も右側もイコールがついていますので、ようは同じチャンクとその前のチャンクがattentionの計算対象になるということです。ただし、あくまでattentionを向ける先は同じハッシュ・バケットです(後程、式で確認しますのでそちらの方がわかりやすいかもしれません)。
そして、その単位ごとにattentionを計算します。
式でおさらい
繰り返しになりますが、もう一度、式で確認してみましょう。
まず、計算方法は以下です。通常のTransformerと変わりません。
$$\begin{align}
o_i = \sum_{ j\in\widetilde{\mathcal{P}}_i}\exp\left(q_i\cdot k_j-m(j,\mathcal{P}_i)-z(i,\mathcal{P}_i)\right)v_j,\\
m(j,\mathcal{P}_i))=\left\{\begin{array}{l,l}
+\infty&\text{if } j\notin \mathcal{P}_i\\
0&\text{otherwise}
\end{array}\right.
\end{align}$$
違うのは、1. attentionを向ける先(マスクを掛けない先)を表す\(\widetilde{\mathcal{P}}_i\)と、2. バッチで処理する集合を表す\(\widetilde{\mathcal{P}}_i\)です。
まず、attentionを向ける集合は、
$$\mathcal{P}_i=\{j:h(q_i)=h(k_j)\}$$
と、同じハッシュ・バケットに入っているベクトルです。それ以外はマスクをします。ハッシュ・バケットの決め方は前述の通りrandom matrixを使って決めます。
そして、バッチで処理する集合は、
$$\widetilde{\mathcal{P}}_i=\left\{j:\left\lfloor \frac{s_i}{m} \right\rfloor-1 \le \left \lfloor\frac{s_j}{m} \right \rfloor\le \left \lfloor\frac{s_i}{m} \right \rfloor\right\}$$
と並べ変えてチャンクに分けましたが、query \(q_i\)が入っているチャンクとその前のチャンクだけで計算します。つまり、通常のTransformerでは、文章全体を一度に処理していましたが、Reformerでは2つのチャンクだけを処理します。
Multi-round LSH attention
今までのやり方だと若干問題が発生するので、工夫がされています。
LSHによりバケットに分けましたが、たまたま出た乱数の値により、似たようなベクトルでも違うハッシュ・バケットに入ってしまうことが想定されます。ですので、複数回ハッシュ・バケットを分けて、一度でも同じバケットに入ったベクトルは同じベケットとみなします。
$$\mathcal{P}_i=\bigcup_{r=1}^{n_{rounds}}\mathcal{P}^{(r)}_i, \hspace{10pt}\text{where }
\mathcal{P}^{(r)}_i=\left\{j:h^{(r)}(q_i)= h^{(r)}(q_j) \right\}$$
これにより、本来はattentionを向けるべきだけど、たまたま乱数の値によりattentionを向けなかったという状況を軽減します。
Causal masking for shared-QK attention
queryとkeyを同じにしているので、必ず自分自身へのattentionが一番大きくなってしまいます。それでは良くないので、Reformerでは自分自身に対してはattentionを向けないようにします。これと上のMulti-round LSH attentionの具体的な計算方法は、論文のAppendixに記載がありますので、興味のある方はご覧ください。
Reversible Transformer
そして、もう一つの工夫がReversible Transformerと呼ばれる仕組みです。ニューラルネットワークでは、バックプロパゲーションのために活性化関数(活性化後)の値を保持しておく必要がありますが、隠れ層の次元が大きく、それをレイヤー数分保持する必要があるため、メモリ使用量が多くなってしまいます。そこで、上位のレイヤーの活性化関数の値から下位の活性化関数の値を計算することができるようにすることで、メモリ使用量をレイヤーの数に依存しないようにするというものです。
具体的には、以下のように計算します。
一般的に、残差結合(Residual Connectin)の計算は、
$$y=x+F(x)$$
ですが、これを以下の図のように修正します。
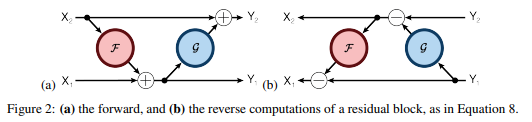
まず、インプットとなる\(x\)を\(x_1\)と\(x_2\)の半分ずつに分けます。そして、
$$y_1 = x_1 + F(x_2)$$
で\(y_1\)を計算し、
$$y_2 =x_2+G(y_1) $$
で\(y_2\)を計算します。そして、\(y_1\)と\(y_2\)を連結したものをアウトプットとします。
バックプロパゲーションでは、前のレイヤーの活性化関数の値、つまり\(x_1\)、\(x_2\)が必要になりますが、
$$x_2 = y_2 - G(y_1)$$
で、\(y_1\)と\(y_2\)の値から\(x_2\)を求め、さらに
$$x_1 = y_1 - F(x_2) $$
で、\(x_1\)も求めることができます。これで、レイヤーのアウトプットからインプット、つまり前のレイヤーのアウトプットが計算できるようになります。
では、これをTransformerに適用しましょう。今回のReformerでは、以下のようにします。
$$\begin{align}
Y_1&=X_1 + \text{Attention}(X_2)\\
Y_2&=X_2 + \text{FeedForward}(Y_1)\\
\end{align}$$
こうすることにより、1つ前のレイヤーの活性化後の値は、
$$X_2 = Y_2 - \text{FeedForward}(Y_1)$$
と
$$X_1 = Y_1 - \text{Attention}(X_2)$$
で求めることができます。こんなことをして大丈夫なのか?と思えますが、あとの実験で精度に対する悪影響がないことが確認できます。
さらに、ReformerではFeedForwardレイヤーでのメモリの使用量を減らすため、チャンクに分けて計算します。
$$\begin{align}
Y_2&=\left[Y_2^{(1)}; \cdots; Y_2^{(c)} \right]\\
&=\left[X_2^{(1)}+\text{FeedForward} \left(Y_1^{(1)}\right) ;\cdots
;X_2^{(c)}+\text{FeedForward} \left(Y_1^{(c)}\right)\right]
\end{align}$$
実験
imagenet64とenwik8-64Kというデータセットで実験しています。enwik8-64Kというデータセットはenwik8データセットを64K個のトークンに分割したものとのことです。
レイヤー数は3、単語の埋め込みや隠れ層の次元は1024、フィードフォワード・レイヤーの次元は4096、head数は8、バッチサイズは8という設定です。
では、まず\(k_j=q_j/||q_j||\)として、query Qとkey Kに同じものを使う影響です。
以下の図の左側のとおり、enwikデータセット(上図)でもimagenet64データセット(下図)でもperplexityの減少速度はほぼ同じで、少しだけreformerの方が減少スピードがはやくなっています。つまり、QとKを同じにすることによる悪影響はなさそうです。
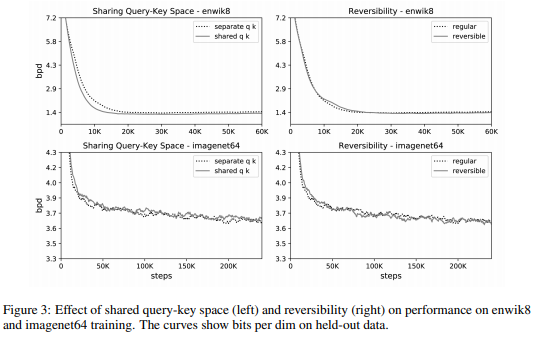
次に、Reversible Transformerを使う影響です。
こちらは上図の右側ですが、どちらのデータセット(上下図)でもほとんど差はなく、Reversible Transformerによってメモリを節約することによる精度への悪影響は見られません。
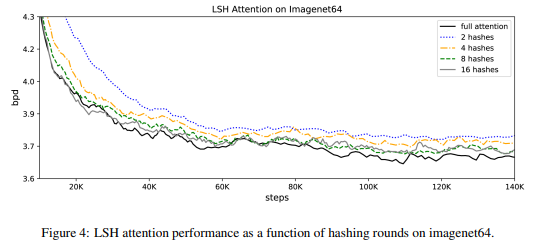
では、ハッシュ・バケットを増やすことにより精度がどう変わるかを見てみましょう。
ハッシュ・バケット数を8程度にすることで、若干下回るものの通常のTransformerであるfull attentionとほぼ同程度の精度になっていることがわかります(ちなみに論文では\(n_{rounds}=8\)と書かれていますが、\(n_{buckets}=8\)の誤植なのかなと思います)。
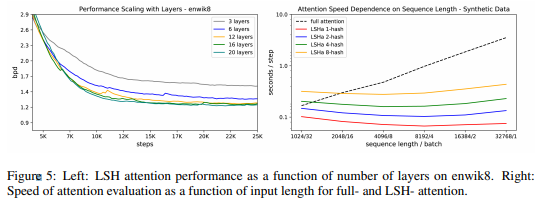
次に計算時間について見てみます。以下の右図は、トータルの単語数を同じにして、文章の長さとバッチ数を調節した場合で、左が文章が短くバッチ数が多い場合、右が文章が長くバッチ数が少ない場合になっています。通常のTransformerであるfull attentionでは、右に行くほど大幅に計算時間が長くなっていますが、ReformerのLSH attentionではハッシュ・バケット数が多くなると計算時間は長くなっていますが、文章数の影響はほとんど受けていません。
左図は、レイヤーを増やすほど精度が向上するというものです。
まとめ
今回は長い文章も取り扱うことができるReformerを紹介しました。
64Kとはいかないまでも2K程度の文章を処理したいということは十分あると思います。それでも通常のTransformerだと非常に遅くなってしまいますので、個人的にはこのReformerは素晴らしいと思います。
なお、Appendixは、実装まで含めた定式化がされており、ここで説明したものより若干詳しくなっています。ただ、それほど変わりませんので読んでいただければ理解できると思いますので、今回は省略させていただきました。ご興味のある方は読んでみてください。

