Batch Normalizationを理解する

今回は、今や当たり前のように使われているBatch Normalization(バッチ正規化)について解説したいと思います。

バッチ正規化は色々な仕組みで使われており、一般的なニューラルネットワークやTabNetなどでも使われています。

まず簡単にBatch Normalizationの特徴をまとめると以下になります。

Batch Normalizationの特徴

インプットとなる特徴量だけを正規化するのではなく、レイヤごとにインプットを正規化する。
その際にミニバッチごとの統計量(平均・分散)を使ってを正規化する。
見込まれる効果は以下。
- 学習が安定する。
- パラメータのスケールや初期値の影響が小さくなる。それにより、高い学習率を設定することが可能になり、学習スピードが速くなる。
- ドロップアウトの必要性を減らすことができる。

色々なテキストに説明がありますが、ここでは、以下の2015年に発表された原論文を参考に解説していきたいと思います。

『Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift』

では見ていきましょう。

1 Batch Normalization
2 補足
- 2.1 より高い学習率を設定
- 2.2 正則化の効果
3 実験結果
4 まとめ
5 おまけ

Batch Normalization

解決したい問題 - Internal Covariate Shift

まず、Batch Normalizationで解決したい問題から説明したいと思います。

例えば、以下の図のように学習データとテストデータで特徴量の分布が違うということがしばしばあります。

この場合、学習データで多くみられた特徴量の値の領域ではテストデータの評価もうまくできる可能性が高いですが、学習データではあまり取らなかった値の領域を取るテストデータが多くなっていると、テストデータをうまく評価することができません。

これをCovariate Shiftと呼び(少し粗い説明にはなっています)、このCovariate Shiftを解決することをDomain Adaption(ドメイン適応)と呼んでいます。

さらに、ディープ・ラーニングではレイヤを何層も積み重ねます。

例えば2番目のレイヤのインプットは1番目のレイヤのアウトプットとなっています。

そこで、1番目のレイヤが学習して、パラメータが変わるとそのアウトプットが変わり、2番目のレイヤのインプットの分布が大きく変わることがあります。

つまり、(ミニ)バッチごとにレイヤへのインプットの分布が変わるということです。

これをInternal Covariate Shiftと呼びます。

直観的にレイヤへのインプットの分布がころころ変わると、学習が安定しないような気がしますね。

Batch Normalizationはこれを解決しようというものです。

解決方法 - Batch Normalization

まず、機械学習ではインプットを特徴量ごとに正規化することが多いです。

Scikit LearnであればStandardScalerなどを使いますね。

これにより、各特徴量の平均をゼロ、標準偏差を1にし、分布の偏りやスケールの影響を排除することができます。

ただ、ディープ・ラーニングではレイヤが複数積み重なったいますので、パラメータが変わるたび、つまりミニバッチごとに各レイヤへのインプットの分布が変わるという問題がありました。

そこで、最初の特徴量のインプットだけでなくレイヤごとにもインプットを正規化しましょう、という発想です。

ただし、インプットの正規化と違う点は、最初のインプットは固定ですので学習前に一度正規化してしまえばよいですが、レイヤへのインプットはパラメータが変わるごとに値が変わります。

ですので、きちんとやろうとするとパラメータを更新する度に学習データ全体をネットワークに流して、各レイヤのインプットを求め、その平均・分散で正規化しなければなりません。

ただ、そこまでするのは効率面からよくありません。

そこで、Batch Normalizationは、全学習データを使うのではなく、ミニバッチごとの統計量を使って、ミニバッチごとにに正規化しましょう、というものです。

これで完全な正規化ではありませんが、簡便的な正規化ができることになります。

あとで説明しますが、実はこれがドロップアウトなどのような正則化の効果も得られます。（ドロップアウトについてはこちら）

アルゴリズム

では、具体的にどのように正規化するかを見ていきましょう。

アルゴリズムは次の通りです。これから少しずつ説明します。

ミニバッチごとの平均・分散を計算

まず、ミニバッチごとに平均・分散を求めます。

$$\begin{align}
\mu_{\mathcal{B}}&=\frac{1}{m}\sum^m_{i=1}x_i\\
\sigma^2_{\mathcal{B}}&=\frac{1}{m}\sum^m_{i=1}(x_i-\mu_{\mathcal{B}})^2
\end{align}$$

$i$はミニバッチ中のサンプルを表す添え字です。

これをレイヤごと、特徴量ごとに行います。

厳密には、レイヤ、特徴量の次元を表す添え字が必要になりますが省略しています。

正規化

そのあとに以下の式で正規化します。

$$\widehat{x}_i=\frac{x_i-\mu_{\mathcal{B}}}{\sqrt{\sigma^2_{\mathcal{B}}+\epsilon}}$$

ここで、分母に$\epsilon$を加えていますが、これは微小値を表し、$\sigma^2_{\mathcal{B}}$が小さい場合に計算を安定されるためです。

こちらもレイヤごと、特徴量ごとに行います。

平均と分散の調整

最後がポイントです。

このまま$\widehat{x}_i$をインプットとして使ってもいいのですが、それでは本来レイヤが持つ非線形性の表現力を失っているかもしれません。

例えば、シグモイド関数だと0付近は線形に近いですが、絶対値が大きくなると非線形になってきます。

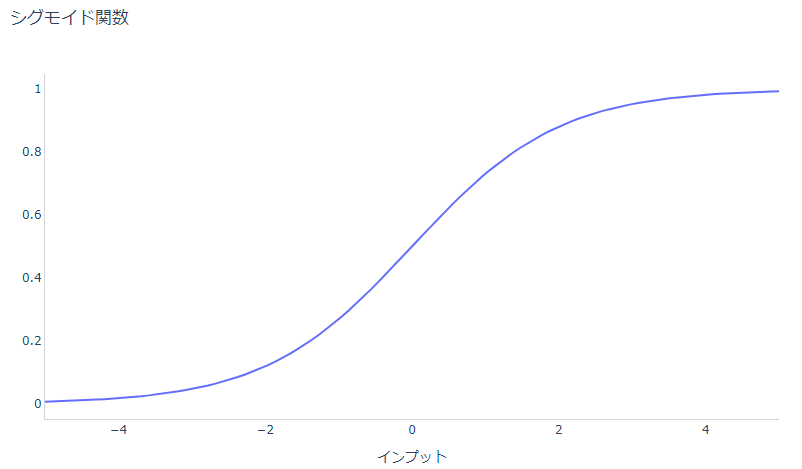
そういった非線形性を入れたいためにシグモイド関数を使っているのですが、レイヤごとに正規化することにより、せっかく学習し表現したその非線形性が失われているかもしれません。

例えば、インプットが-1から1の範囲ではシグモイド関数はほぼ線形になっています。

本当は以下のように非線形な処理が入った方がよいかもしれません。

ReLUなどでも同様の考え方です。

そこで、インプット$\widehat{x}_i$の分布を変化させます。

具体的には平均に対応するパラメータ$\beta$と標準偏差に対応するパラメータ$\gamma$を導入し、$\widehat{x}_i$を$\beta$の分だけ横にシフトさせ、$\gamma$でスケールを変更します。

$$y_i=\gamma\widehat{x}_i+\beta$$

ここで重要なのは、この$\beta$、$\gamma$は学習するパラメータということです。

例えば、$\beta=0$、$\gamma=1$に近ければ単純に正規化したものと近く、それ以外であればスケールやシフトすることで必要な非線形性を学習していると言えます。

全体のアルゴリズム

今まではミニバッチを使った正規化の方法について見てきました。

ここでは、Batch Normalizationを使って学習、推論をどのように行うかを見ていきましょう。

全体のアルゴリズムは以下です。

少しややこしいので学習フェーズでと推論フェーズで分けて見てみましょう。

学習時

ではまず、学習時のアルゴリズムを一つずつ見ていきます(オレンジで囲まれている箇所です)。

$N$はネットワーク全体を表します。

まず、2-5行目でバッチ正規化を行っています。

各特徴量ごとに$x^{(k)}$を正規化した$y^{(k)}$に変換します(3行目)。

$k$は何番目の特徴量かを表しています。

そして、各レイヤでインプットを$x^{(k)}$を$y^{(k)}$に置き換えます(4行目)。

続いて、ニューラル・ネットワークのパラメータ$\Theta$とBatch Normalizationのパラメータ$\beta^{(k)}$と$\gamma^{(k)}$を更新し、損失関数を最小化します(6行目)。

最終的に得られたネットワーク$N_\text{BN}^\text{tr}$を推論用のネットワーク$N_\text{BN}^\text{tr}$とします(7行目)。

以上のように、学習方法は通常のニューラル・ネットワークの学習とあまり変わりません。

推論時

では、ネットワークの学習ができたので、実際にテストデータや実際のデータを使って推論するフェーズになります。

このとき、学習済みパラメータ$\Theta$、$\beta^{(k)}$、$\gamma^{(k)}$は固定します。

ここで問題が発生します。

学習時には以下のようにミニバッチごとに平均・分散を求め、それを使って正規化していました。

$$\begin{align}
\mu_{\mathcal{B}}&=\frac{1}{m}\sum^m_{i=1}x_i\\
\sigma^2_{\mathcal{B}}&=\frac{1}{m}\sum^m_{i=1}(x_i-\mu_{\mathcal{B}})^2\\
\widehat{x}_i&=\frac{x_i-\mu_{\mathcal{B}}}{\sqrt{\sigma^2_{\mathcal{B}}+\epsilon}}
\end{align}$$

しかし、推論フェーズではそのようには、推論したいサンプルごとに求めた平均・分散を使うことはよくありません。

なぜなら、例えばサンプルが一つだと平均・分散は計算できませんし、もし複数のサンプルをまとめて計算するとしても、サンプルをどう取るかによって平均・分散が変わってしまうので、推論結果が変わってしまいます。

推論時の結果はサンプル集団の取り方にかかわらず確定的に出力するようにしないといけません。

そこで、学習サンプル全体の平均・分散を使うようにします。

どのようにするか見ていきましょう。

オレンジで囲んだところが推論フェーズです。

10行目が母集団の平均・分散を求めている箇所です。

バッチごとの平均の平均を母集団の平均とし、バッチごとの分散の平均を母集団の分散としています。

$$\begin{align}
\mathbb{E}[x]&=\mathbb{E}_\mathcal{B}[\mu_\mathcal{B}]\\
\text{Var}[x]&=\frac{m}{m-1}\mathbb{E}_\mathcal{B}[\sigma^2_\mathcal{B}]
\end{align}$$

ここで、分散の$m/(1-m)$は分散を不変推定量にするものです。

詳しくは統計の本(『基本統計学』や『入門数理統計学』などがオススメです)をご参照ください。

実際の計算は移動平均を使って行います。

学習時に以下のようにして、$\mathbb{E}[x]$と$\text{Var}[x]$を保持しておきます。

$$\begin{align}
\mathbb{E}[x] &\leftarrow \eta \times \mathbb{E}[x] + (1-\eta)\times \mu_{\mathcal{B}}\\
\text{Var}[x] &\leftarrow \eta \times \text{Var}[x] + (1-\eta)\times \sigma^2_{\mathcal{B}}
\end{align}$$

$\eta$は0.99や0.9などといった値を使い、これが大きいほど新たな$\mu_{\mathcal{B}}$が寄与する分が減り、少しずつ更新されていくことになります。

例えば、以下のような形で、9割は現状の$\mathbb{E}[x]$や$\text{Var}[x]$を使い、1割は$\mu_\mathcal{B}$は$\sigma^2_\mathcal{B}$を使って更新するイメージです。

$$\begin{align}
\mathbb{E}[x] &\leftarrow 0.9 \times \mathbb{E}[x] + 0.1 \times \mu_{\mathcal{B}}\\
\text{Var}[x] &\leftarrow 0.9 \times \text{Var}[x] + 0.1\times \sigma^2_{\mathcal{B}}
\end{align}$$

そして、その学習時に計算した平均と分散とスケーリング・パラメータ$\beta$、$\gamma$を使って、以下の式で最終な推論を行います。

$$\begin{align}
y&=\gamma\cdot \widehat{x}+\beta\\
&=\gamma\frac{x-\mathbb{E}[x]}{\sqrt{\text{Var}[x]+\epsilon}}+\beta\\
&=\frac{\gamma}{\sqrt{\text{Var}[x]+\epsilon}}\cdot x+\left(\beta - \frac{\gamma \mathbb{E}[x]}{\sqrt{\text{Var}[x]+\epsilon}} \right)
\end{align}$$

なおプログラムを実際に見た方がわかりやすいという方はこちらの記事をご参照ください。

『Implementing Batch Normalization in Python』

正規化するタイミング

あと、1点考慮する点があります。

全結合層は以下のように、インプット$u$に対して、行列$w$を掛けてバイアス$b$を足し、その後に活性化関数$g$で非線形な変換を行います。

$$z=g(Wu+b)$$

そこで、どこのタイミングで正規化するか？という点で、以下の2つが考えられます。

シンプルに前の層から来た$u$を正規化する
全結合層を通して、活性化関数の前に正規化する

論文では、後者の「全結合の後、活性化関数の前」が選択されています。

つまり、

$$z=g(\text{BN}(Wu))$$

とします。

補足

Batch Normalizationの仕組みは以上です。

ここでは、それ以外の補足的な事項について解説したいと思います。

より高い学習率を設定

Batch Normalizationを行うことにより、より高い学習率を設定することが可能になりますが、この理由を説明します。

より高い学習率を使うと、パラメータがより大きく動くことになります。

そして、パラメータが大きいと勾配が大きくなり、発散してしまうことがあります。

$W$を$a$倍した場合どうなるでしょう。

Batch Normalizationを使うと、$Wu$に$a$を掛けても、どちらにしてもスケールが調整されるので、

$$\text{BN}(Wu)=\text{BN}((aW)u)$$

が成立します。

したがって、前のレイヤに流す勾配は、

$$\begin{align}
\frac{\partial\text{BN}((aW)u)}{\partial u}=\frac{\partial\text{BN}((W)u)}{\partial u}
\end{align}$$

となって、パラメータが大きくなっても前のレイヤに流す勾配は変わりません。

そして、$W$を更新するための勾配は

$$\begin{align}
\frac{\partial\text{BN}((aW)u)}{\partial aW}=\frac{\partial\text{BN}((W)u)}{\partial aW}=\frac{1}{a}\frac{\partial\text{BN}((W)u)}{\partial W}
\end{align}$$

と逆に$1/a$に小さくなります。

これにより、大きな学習率を設定してもパラメータの増減が安定するということになります。