さて、今日はみんな大好き Word2Vec を解説したいと思います。
Word2Vec の結果を見たり、遊んでみたりするのは、非常に楽しいですので、まずはざっくり概要を解説したいと思います。
Word2Vecとは
Word2Vec とは、2013年に当時 Google にいた Thomas Mikolov らが書いた以下の論文による、単語の埋め込み表現を計算するモデルです。
https://arxiv.org/abs/1301.3781
単語の埋め込み表現とは、単語をその単語の意味を表現する低次元のベクトルに変換することを言います。
例えば、「犬」や「猫」をある128次元のベクトル(数字の列)で表すことを言います。
このとき、「犬」と「猫」は同じ動物ですので、これらの単語の埋め込み表現は似ているようになります。
一方で、それらと例えば「パソコン」といった関連性の低い単語は、「犬」、「猫」の埋め込み表現とは大きく違ってきます。
では、この埋め込み表現はどうやって得るのでしょうか?
Word2Vec では、これを非常にシンプルなニューラルネットワークで獲得しています。
埋め込み表現の計算
Word2Vec では、文章の単語の並びから、間にある単語を予測する(CBOW モデル)、もしくはある単語から周りにある単語を予測する(Skipgram モデル)というタスクを解くことで、獲得することができます。
ですので、CBOW モデルや Skipgram モデルは間にある単語や周りにある単語を正解ラベルとした教師あり学習になります。
CBOWモデル
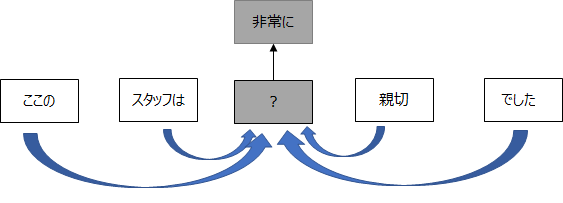
CBOW モデルは、周辺の単語から間にある単語を予測します。
周辺の単語数を“ウィンドウ”と呼び、下の例ですとそれぞれ左右で2個ずつ取っていることから、ウィンドウは2となります。
また、ここでの周辺の単語を“コンテキスト”、間の当てる単語を“ターゲット”といいます。
Skipgramモデル
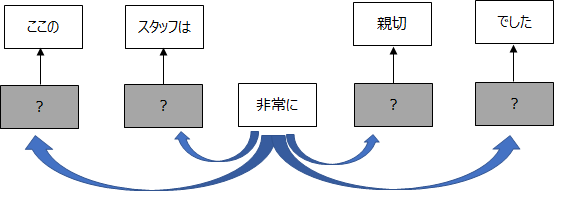
Skipgram モデルは、CBOW モデルとは逆である単語から周辺の単語を予測します。
何となく CBOW モデルより難しそうですよね。
後述しますが、実はこれが精度にも影響してきます。
では、具体的にどうやって分散表現を獲得するかというと、非常にシンプルなニューラル・ネットワークを使用します。
CBOW モデルでざっくり説明しますと、インプットは、単語を表す one-hot ベクトルです。
例えば、「スタッフ」「親切」がコンテキストで、「非常に」がターゲットの場合、インプットは「スタッフ」「親切」を表す one-hot ベクトルです。
つまり、「スタッフ」を表す箇所だけ1でそれ以外は0のベクトルです。
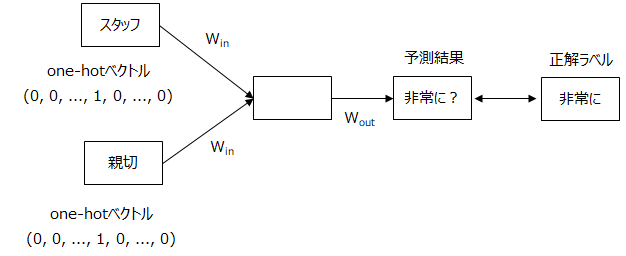
そして、この2つのベクトルに、\(W_{in}\) という行列をかけて、平均を取ります。
これがいわゆるエンコーディングです。
そして、そのエンコーディングされたものに対し、\(W_{out}\)をまたかけて、ソフトマックス関数で、間の単語を予測します。
このときの、\( W_{in} \) が単語の分散表現になります。
本当はもう少し議論があり、ソフトマックス関数の計算量を減らすための工夫や、 \( W_{in}\) と \(W_{out}\) のどちらを分散表現とすべきかといった議論もありますが、ここでは割愛したいと思います。
興味がある方は論文や記事の最後に紹介している書籍を参考にしていただければと思います。
Word2Vecで遊んでみる
本記事では Word2Vec の理論的な面を解説していますが、以下の記事でキャンプ場の口コミを使って Word2Vec により埋め込み表現を求め、似たような単語を見てみたり、単語マップを作製したりして遊んでいます。
イメージがわきやすいと思いますので、ぜひご覧ください!
Word2Vecの利用方法
Word2Vec で獲得した単語の埋め込み表現は主に、特定のタスクを解くための埋め込みレイヤ( Embedding layer )の初期値として使われることが多いです。
つまり、Wikipedia やニュースコーパスなどの大きな(たくさんの単語が網羅される)データをもとに単語の埋め込み表現を学習させます。
そして、そういった埋め込み表現は公開されています。
その後、例えばセンチメント分析など特定のタスクを解くために利用します。
これによって、あらかじめ単語の精度の高い埋め込み表現がわかっているので、収束がはやく、学習データにはなくて、テストデータにのみ出てくる単語の埋め込み表現もわかっているため、予測モデルの精度が上がることが期待されます。
まとめ
今回は Word2Vec を簡単に解説しました。
もっと詳しく知りたいという方は以下の書籍を参考にしていただければと思います。
こちらはスクラッチで Word2Vec を実装したり、再帰的ニューラルネットワークやアテンション・メカニズムを実装していますので、細かいところまでしっかり理解できると思います。
説明も非常に丁寧なので、そこまで苦労することなく楽しく読むことができると思いますので、入門者にはすごくオススメの一冊です。
では!
