ディープラーニングで非常に重要な技術である正規化ですが、今回はその正規化手法の一つであるInstance Normalizationを解説したいと思います。
以下の図は各正規化手法の考え方をまとめたものです。
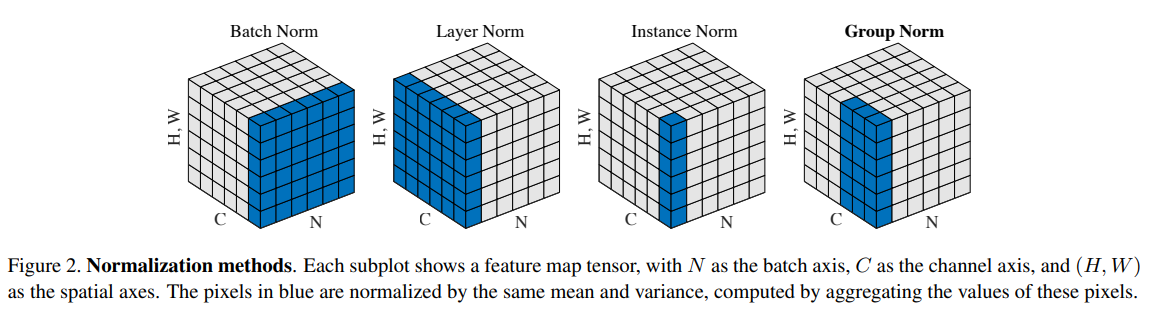
右から2番目が今回説明するInstance Normalizationで、Batch Normalizationを理解していれば非常に簡単です。
しかしながら、もっと根本的な、なぜこういう正規化をするか?といった背景も含めて解説していきたいと思います。
論文はこちらになります。
『Instance Normalization: The Missing Ingredient for Fast Stylization』
では、さっそく見ていきましょう。
Instance Normalizationの背景
Instance Normalizationは2016年にStyle Transfer(スタイル変換)の仕組みの一部として提案されました。
Style Transferは以下のように、絵の内容を表すcontent image(左側)と絵のスタイル・画風を表すstyle image(真ん中)の2つの画像を入力して、content imageの内容でstyle imageのスタイルを持つ絵(右側)を生成するというものです。

従来、このStyle TransferではBatch Normalization(バッチ正規化)を正規化手法として使用していました。
Batch Normalizationについては以下をご参照ください。
Deep Learningの学習において非常に成功を収めたBatch Normalizationですが欠点があります。
それは、Batch Normalizationはミニバッチごとに平均・分散で正規化することから、“ミニバッチのサイズが小さいと推定される平均・分散が正確ではなくなり、学習が安定しない”という点です。
例えば、ミニバッチのサイズが4とかだと平均・分散は安定せず、ミニバッチの選ばれ方により値がすごくぶれることになります。
特に最近はモデルが巨大化しているのでミニバッチ数をそれほど大きくできない場合も多いです。
Instance Normalizationはこれを解決することができます。
また、これはのちに出てくるGroup Normalization(グループ正規化)(『Group Normalization(グループ正規化)を理解する』をご参照)でも改善するポイントでもあります。
あと、Instance Normalizationを使う動機で重要な点がもう一つあります。
例えば、以下のような画像です。

まず左の画像がcontent imageで右側がstyle imageを組み合わせて生成された画像になります。
見てわかる通りcontent imageの上段と下段はまったく同じ人の画像ですが、上段の方がコントラストがはっきりしていて、下段はコントラストが低くなっています。
そして右側の生成された画像ですが、少しわかりにくいですが、上段と下段で若干違うコントラストになっているのがわかります。
ここでの問題は“コントラストなどのスタイルはcontent imageではなくstyle imageで決めるべき”という点です。
つまり、同じ人の同じ画像のcontent imageで、同じstyle imageを適用した場合、ほとんど同じ画像が生成されて欲しいというものです。
そこで、考えられたのがInstance Normalizationです。
ここまででいったんポイントをまとめておきます。
- Batch Normalizationはミニバッチ中のサンプル数が少なくなると平均・分散の推定が不安定になり、良い画像を生成できなくなる。
- Style transferではコントラストの情報はstyle imageの情報を使い、content image側の情報は使いたくない。
Instance Normalizationとは
Batch NormalizationとInstance Normalizationの違いを見ていきます。
以下の有名な図で説明します。

Batch Normalizationは一番左の立方体ですが、何の平均・分散を取るかというと「高さ(H)、幅(W)、バッチ(N)」になります。
つまり、ある\(c\)番目のチャネルについては、ミニバッチ中のサンプルすべてを使って、そのチャネル\(c\)の高さ(縦)・幅(横)の値の平均・分散を計算して、正規化します。
一方で、Instance Normalizationは右から2番目ですが、バッチ(N)の軸を外して「高さ(H)と幅(W)」の平均・分散を計算します。
つまり、インスタンス(特定のサンプル)ごとに平均・分散を計算するということです。
なぜこうしたかというと、上記で説明した“コントラストなどのスタイルはcontent imageではなくstyle imageで決めるべき”という考え方です。
言い換えると、“content imageはコントラストの情報を捨てるべき”という考え方になります。
Batch Normalizationはバッチ全体で正規化していたので、各サンプルのコントラスト情報は残ります。
例えば、バッチ全体で平均0・分散1に正規化されても、コントラストが強い画像1枚を取り出してみると、正規化後の分散は1よりも大きくなり、正規化後もコントラストが強くなります。
一方で、Instance Normalizationはそのサンプルの縦・横のピクセル値の平均・分散で正規化することから、すべてのサンプルがそれぞれ平均0・分散1に正規化されることになります。
これがInstance Normalizationが“contrast normalization"(コントラスト正規化)とも呼ばれる理由です。
- 各サンプルにおける平均・分散を使うことで、ミニバッチ中のサンプル数が少なくても問題がない。
- 各サンプルの平均・分散で正規化されるので、すべての画像が同じようなコントラストになるように変換される。
平均・分散の計算方法
では、具体的にどのように平均・分散を計算するか確認しましょう。
Batch Normalizationとの違いをはっきりさせるために、Batch Normalizationから見ていきます。
Batch Normalization
Batch Normalizationは以下の図のようにN(ミニバッチ)、W(幅)、H(高さ)方向で平均・分散を計算します。
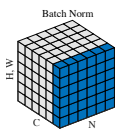
数式で表すと以下のようになります。
\(x\in\mathbb{R}^{T\times C \times W \times H}\)とします。
ここで\(T\)はバッチの中の画像の数、\(C\)はチャネル数、\(W\)は幅、\(H\)は高さを表します。
そして、以下のように計算します。
\begin{align}
y_{tijk}&= \frac{x_{tijk}-\mu_i}{\sqrt{\sigma^2_i+\epsilon}} \\
\mu_{i}&= \frac{1}{HWT}\sum^{T}_{t=1} \sum^{W}_{l=1} \sum^{H}_{m=1} x_{tilm} \\
\sigma^2_{i}&= \frac{1}{HWT}\sum^{T}_{t=1} \sum^{W}_{l=1} \sum^{H}_{m=1} \left( x_{tilm} - \mu_i\right)^2 \\
\end{align}
\(T\)、\(W\)、\(H\)で平均を取っていますね。
平均・分散の添え字が\(i\)になっており、チャネルごとに1つの平均・分散が求まるということを表しています。
Instance Normalization
では、本題のInstance Normalizationです。
Instance Normalizationは以下の図のようにミニバッチの平均は取らず、W(幅)、H(高さ)方向で平均・分散を計算します。
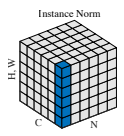
数式で書くと以下のようになります。
\begin{align}
y_{tijk}&= \frac{x_{tijk}-\mu_{ti}}{\sqrt{\sigma^2_{ti}+\epsilon}} \\
\mu_{ti}&= \frac{1}{HW}\sum^{W}_{l=1} \sum^{H}_{m=1} x_{tilm} \\
\sigma^2_{ti}&= \frac{1}{HW}\sum^{W}_{l=1} \sum^{H}_{m=1} \left( x_{tilm} - \mu_{it}\right)^2 \\
\end{align}
平均・分散の添え字が\(t\)と\(i\)になっていますので、サンプルごと、チャネルごとに1つの平均・分散が求まるということを表しています。
まとめ
以上がInstance Normalizationの説明になります。
計算方法は非常に簡単ですね。
また背後にある背景についてもご理解いただけたかと思います。
他にも時系列モデルでよく使われるLayer Normalizationもあり、それぞれ特徴がありますので、背景がわかっているとよく理解できますね。
次はGroup Normalizationについて解説したいと思います!(もうしました↓)
では!


