DiffusionモデルをPyTorchで実装する③ ~ 学習編

ここまでで、Diffusionモデルの仕組みの実装とDiffusionモデルで使われているニューラルネットワークであるU-Netの実装が完了しました。

これまでの記事はこちらです↓

これまでの記事

Diffusionモデルの論文解説
『【論文解説】Diffusion Modelを理解する』

Diffusionモデルの実装
『DiffusionモデルをPyTorchで実装する① ~ Diffusionモデル実装編』

U-Netの実装
『DiffusionモデルをPyTorchで実装する② ~ U-Net実装編』

今回はこれらの仕組みを使って、Fashion MNISTデータセットで実際にモデルを学習させたいと思います。

最終的に画像を生成できるようになりますが、出来上がりには期待しないでいただければと思います(笑)

ただ、これらを自分で実装することで、しっかりとDiffusionモデルを理解することができ、また自分でデータを集めてモデルを構築することもできるようになると思います！

では、実装してきましょう。

1 準備
2 学習
- 2.1 画像の生成
3 まとめ
4 (ご参考) Hugging Faceのコード

準備

モジュールのインポート

まずは必要なモジュールをインポートします。

from datasets import load_dataset # hugging faceのdatasetを使う

from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
from torchvision import transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader

from torch.optim import Adam

from pathlib import Path

pathlibはPythonに標準ライブラリに入っているモジュールで、os.pathと同じような機能を持つ、より便利なモジュールです。

データセットの準備

データセットはFashion MNISTを使います。

Fashion MNISTは白黒画像で、以下のように服や靴などファッションに関する画像のデータセットです。

hugging faceのdatasetを利用するので、必要に応じてインストールしてください。

(hugging faceのdatasetの詳細はこちらです)

まず、datasets.load_dataset()でfashion MNISTのデータを取得します。

dataset = load_dataset("fashion_mnist")

画像のサイズ、チャネル数(白黒なので1)、バッチサイズを設定します。

image_size = 28
channels = 1
batch_size = 128

torchvisionのtransformsを使って画像の前処理を行います。

transform = Compose([
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor(),
    transforms.Lambda(lambda t: (t * 2) - 1)
])

2行目のRandomHorizontalFlip()でランダムに左右を反転させデータを増やしています。

そして、3行目のToTensorで画像データをテンソルに変換し、最後に4行目で[0, 1]の値を[-1, 1]に変換しています。

続いて、今作成したtransformでテンソルに変換し、"pixel_values"というキーを持つ辞書型変数を作成するコードを実装します。

ラベルは使用しないので除いています。

def transforms_data(examples):
  # 画像データを数値データに変換
  examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
  del examples["image"]
  return examples

transformed_dataset = dataset.with_transform(transforms_data).remove_columns("label")

# データローダーの作成
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)

ちなみに、3行目のimage.convert("L")はカラーの画像をグレースケールにするためのものなので、今回のFashion MNISTデータではなくても問題ありません。

最後に、生成した画像を保存するためのフォルダを設定します。

画像を保存しない人はこちらはなくても大丈夫です。

results_folder = Path("保存したいフォルダ/results")
results_folder.mkdir(exist_ok=True)

モデルの作成

では、モデルを生成しましょう。

GPUが使える場合はdeviceに"cuda"を指定します。

device = "cuda" if torch.cuda.is_available() else "cpu"

前回と同じようにU-Netモデルのインスタンスを生成します。

model = Unet(
    dim=image_size,
    channels=channels,
    dim_mults=(1, 2, 4,),
    resnet_block_groups=4,
)
model.to(device)

dim_multsはダウンサンプル時にチャネルのサイズを何倍にしていくか？を表します。

optimizerはAdamを指定します。

optimizer = Adam(model.parameters(), lr=1e-3)

学習

では、実際に学習していきましょう。

学習は10エポックとします。(5エポックとかでも大丈夫です)

epochs = 10

以下のコードで学習をします。

for epoch in range(epochs):
  for step, batch in enumerate(dataloader):
    optimizer.zero_grad()

    batch_size = batch["pixel_values"].shape[0]
    batch = batch["pixel_values"].to(device) # データを設定

    t = torch.randint(0, timesteps, (batch_size,), device=device).long() # タイムステップ情報をバッチごとにランダムに与える
    loss = p_losses(model, batch, t) # 画像を生成し損失を計算

    if step % 100 == 0: # 表示
      print("Loss", loss.item())

    loss.backward() # 勾配の計算
    optimizer.step() # パラメータの更新

  # 画像の生成
  samples = sample(model, image_size=image_size, batch_size=25, channels=channels)
  save_image(torch.from_numpy(samples[-1]), str(results_folder / f'sample-{epoch}.png'), nrow=5)

8行目の時点情報を設定している箇所について補足します。

t = torch.randint(0, timesteps, (batch_size,), device=device).long() # タイムステップ情報

損失関数(目的関数)は以下で表されますので、$t$、${\bf{x}}$、$\epsilon$について期待値を取ります。

$$L_\text{simple}(\theta)=\mathbb{E}_{{\bf{t}}, {\bf{x}}_0, {\bf{\epsilon}}}\left[\| \epsilon-\epsilon_\theta \left({\bf{x}}_t, t \right) \|^2\right]$$

そこで、すべてのタイムステップ$t$で計算するのではなく、ランダムに1点だけ選び期待値計算を行います。

最後の2行はサンプルを生成し、その結果をフォルダに保存しています。

 画像の生成
  samples = sample(model, image_size=image_size, batch_size=25, channels=channels)
  save_image(torch.from_numpy(samples[-1]), str(results_folder / f'sample-{epoch}.png'), nrow=5)

保存しない場合は不要です。

Hugging Faceの公式ブログのコードはうまく動きませんので修正しています。

(ただ、適当に1エポックごとに最終ステップの画像のみを保存するようにしています)

実行してLossが減っていれば問題なさそうです。

これで学習が終わりました。

画像の生成

学習したモデルを使って画像を生成してみましょう。

前回作成したsample()という関数を呼び出すことで、batch_size × timestep分の画像が生成されます。

samples = sample(model, image_size=image_size, batch_size=64, channels=channels)

random_indexで指定したバッチの画像を表示します。

random_index = 1
plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels).squeeze(), cmap="gray")

samples[-1]としているのは最終ステップの画像のみを表示しています。

実際に出来上がった画像のうち、比較的うまくいっている画像には以下のようなものがあります。

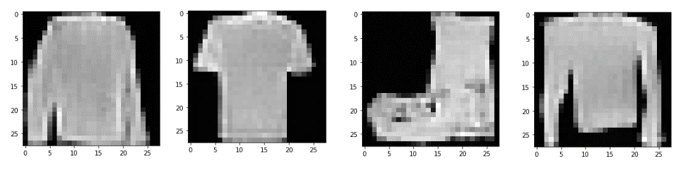
それほどうまくいっているという感じではありませんが、こんなものなのでしょうかね。

また、このようにうまくいっていない画像も多数あります。

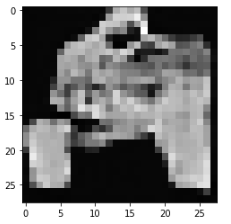
あと、生成された画像には長袖のTシャツが多いように思えます。

以下では、上記の左から2番目のTシャツを時点が進むにつれ、キレイな画像が生成されていく様子を描画しています。

ランダムなノイズから出発し、reverse processで画像が生成されていく様子

左上がランダムなノイズでそこから右下に向かって、reverse processによりキレイなTシャツが生成されていく様子がわかります。

以上で、実装は終了です！

まとめ

今まで3回に渡ってをDiffusionモデルを実装してきました。

とうとう実際の画像を使って学習し、画像を生成することができました。

ただ、これだけだとDALL-E2やGLIDEのようにDiffusionモデルの威力がわかりませんね。

一度、興味のあるデータセットを集めてモデルを学習してみてはいかがでしょうか？

私も試してみたいと思っています。

また、この後に$\Sigma_\theta$を学習したり、ラベルに従って画像を生成するモデルなどが提案されていますので、そのあたりの論文についても解説していければと思っています。

では！

(ご参考) Hugging Faceのコード

今回はわかりやすくするためにHugging Faceのコードを少し単純化しています。

ご参考までに、いくつかの主な部分について、元のコードを説明を付けて掲載しておきます。

損失関数

損失関数は論文の通りL2損失を使っていましたが、Hugging FaceのコードではL1, Huber損失関数も実装しています。

厳密にはSmooth L1損失というものを使っています。

Smooth L1損失関数については以下をご参照ください。

『PyTorch Smooth L1 loss』

実際には以下のような形でloss_typeを選ぶことができる損失関数にしています。

def p_losses(denoise_model, x_start, t, noise=None, loss_type="huber"):
  if noise is None:
    noise = torch.randn_like(x_start)

  x_noisy = q_sample(x_start=x_start, t=t, sqrt_alphas_cumprod=sqrt_alphas_cumprod, 
                     sqrt_one_minus_alphas_cumprod=sqrt_one_minus_alphas_cumprod,
                     noise=noise)
  predicted_noise = denoise_model(x_noisy, t)

  if loss_type == 'l1':
    loss = F.l1_loss(noise, predicted_noise)
  elif loss_type == 'l2':
    loss = F.l2_loss(noise, predicted_noise)
  elif loss_type == 'huber':
    loss = F.smooth_l1_loss(noise, predicted_noise)
  else:
    raise NotImplementedError()
  
  return loss

$\beta_t$の設定

このブログでは、元の論文の通り$\beta_t$はタイムステップに線形にしていました。

Hugging Faceのブログでは、以下の論文をもとにcosine関数を使ったスケジュールなどを試しています。

『Improved Denoising Diffusion Probabilistic Models』

cosine関数による$\beta_t$は以下のような式に従います。

\begin{align}
\beta_t&=1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}} \tag{1}\\
\bar{\alpha}_t&=\frac{f(t)}{f(0)}, \tag{2} \\
f(t)&=\cos\left(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2}\right)^2 \tag{3}
\end{align}

実装は以下です。

def cosine_beta_schedule(timesteps, s=0.008):
  steps = timesteps + 1
  x = torch.linspace(0, timesteps, steps)
  alphas_cumprod = torch.cos(((x / timesteps) + s) / ( 1 + s ) * torch.pi * 0.5) ** 2 # (3)式
  alphas_cumprod = alphas_cumprod / alphas_cumprod[0] # (2)式の\alpha_t
  betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1]) # (1)式
  return torch.clip(betas, 0.0001, 0.9999) # 最大・最小を設定

他にも、quadratic beta scheduleやsigmoid beta scheduleというものが作成されています。

# quadratic beta schedule
def quadratic_beta_schedule(timesteps):
  beta_start = 0.0001
  beta_end = 0.02
  return torch.linspace(beta_start**0.5, beta_end**0.5, timesteps) ** 2

# sigmoid beta schedule
def sigmoid_beta_schedule(timesteps): 
  beta_start = 0.0001
  beta_end = 0.02
  betas = torch.linspace(-6, 6, timesteps)
  return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start

ConvNeXTブロック

本記事では、通常のResNetブロックを使いましたが、Hugging FaceのブログではConvNeXTブロックというものを使っています。

『A ConvNet for the 2020s』

しかしながら、Hugging Faceが参考にしたコードの作者もConvNeXTブロックは使わなくなったりと、効果は確認する必要がありそうです。

参考までにコードを載せておきます。

class ConvNextBlock(nn.Module):
  def __init__(self, dim, dim_out, *, time_emb_dim=None, mult=2, norm=True):
    super().__init__()
    if exists(time_emb_dim):
      self.mlp = (
          nn.Sequential(
              nn.GELU(),
              nn.Linear(time_emb_dim, dim)          
          )
      )
    else:
      self.mlp = (None)

    self.ds_conv = nn.Conv2d(dim, dim, 7, padding=3, groups=dim)
    self.net = nn.Sequential(
        nn.GroupNorm(1, dim) if norm else nn.Identity(),
        nn.Conv2d(dim, dim_out * mult, 3, padding=1),
        nn.GELU(),
        nn.GroupNorm(1, dim_out * mult),
        nn.Conv2d(dim_out * mult, dim_out, 3, padding=1),
    )

    if dim != dim_out:
      self.res_conv = nn.Conv2d(dim, dim_out, 1)
    else:
      self.res_conv = nn.Identity()


  def forward(self, x, time_emb=None):
    h = self.ds_conv(x)

    if exists(self.mlp) and exists(time_emb):
      assert exists(time_emb)
      condition = self.mlp(time_emb)
      h += rearrange(condition, "b c -> b c 1 1")

    h = self.net(h)
    return h + self.res_conv(x)