今回は畳み込みニューラルネットワーク(Convolutional Neural Network; CNN)で使われている畳み込み演算(convolution, コンボルーション)や、GAN(Generative Adversarial Network)で使われている転置畳み込み演算(transposed convolution)について、できるだけわかりやすく解説したいと思います。
計算方法を見れば名前のイメージほど難しくありませんので、まずはここから理解していきましょう!
目次
畳み込み演算とは
畳み込み演算は主に画像処理でよく使われる畳み込みニューラルネットワークで利用されている演算方法です。
画像は一点だけを見ても色しかわからず、何の画像かという情報はありません。
ですので、画像では隣り合った点との関係が重要になってきます。
そこで畳み込み演算は、範囲に対して演算を行うものです。
例えば5x5の範囲に対して演算処理を行い、その5x5の範囲について、どんな特徴を持つか?といった情報を計算するものです。
では具体的な計算方法を見ていきましょう。
まずは、通常の畳み込みの計算方法です。
畳み込み演算はインプットデータと畳み込みに利用するカーネルと呼ばれるもので計算します。
このカーネルがCNNなどで学習するパラメータになります。
計算例
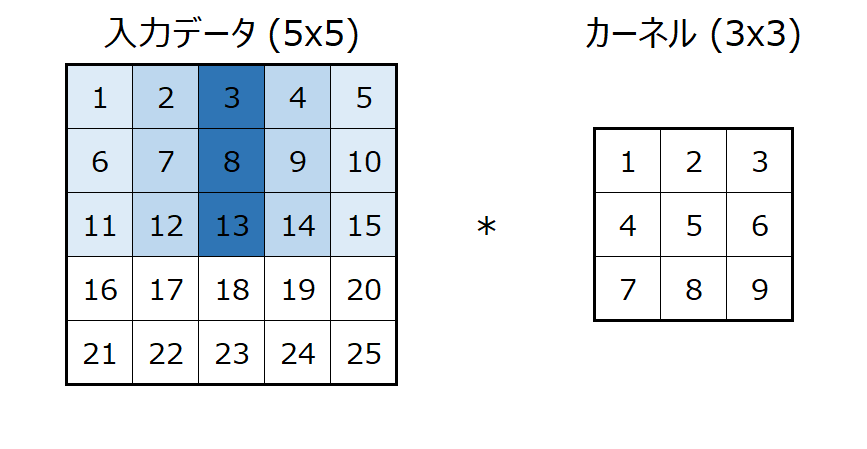
5x5のインプットデータに3x3のカーネルを使って畳み込み演算をする場合を考えます。
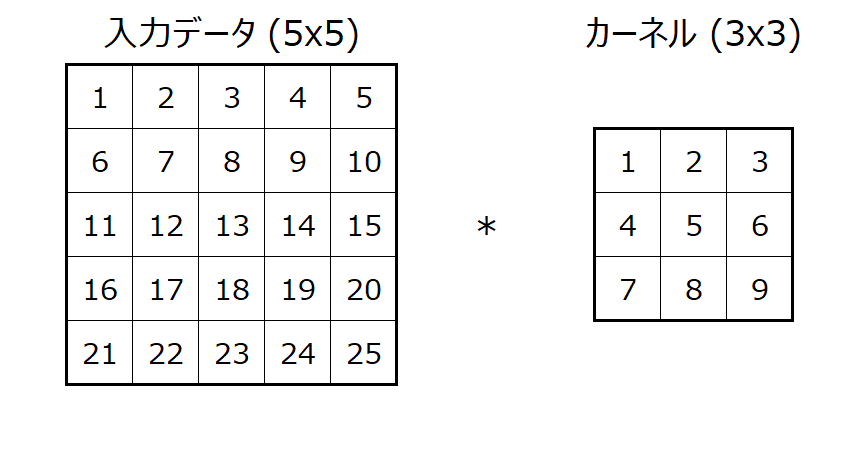
あとで詳しく説明しますが、5x5の入力に3x3のカーネルを適用するとアウトプットは3x3になります。
これについてはのちほど説明しますので、まずはそういうものと考えてもらえればと思います。
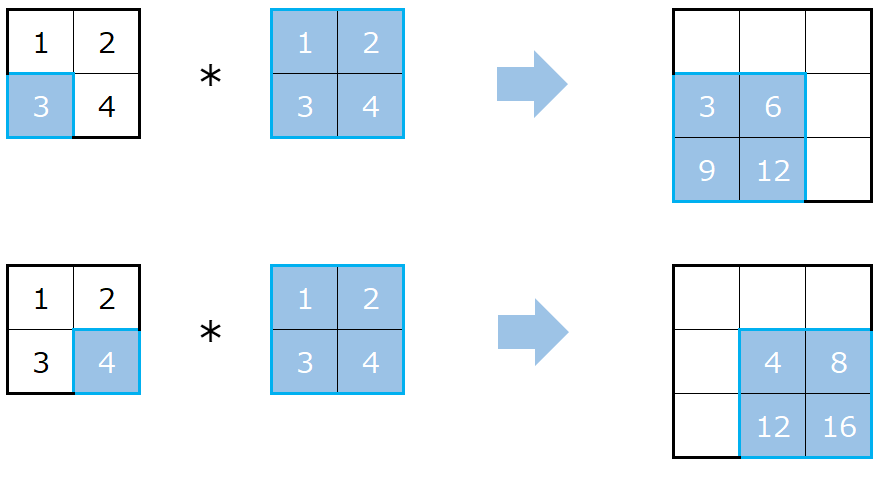
では、畳み込みの計算方法です。
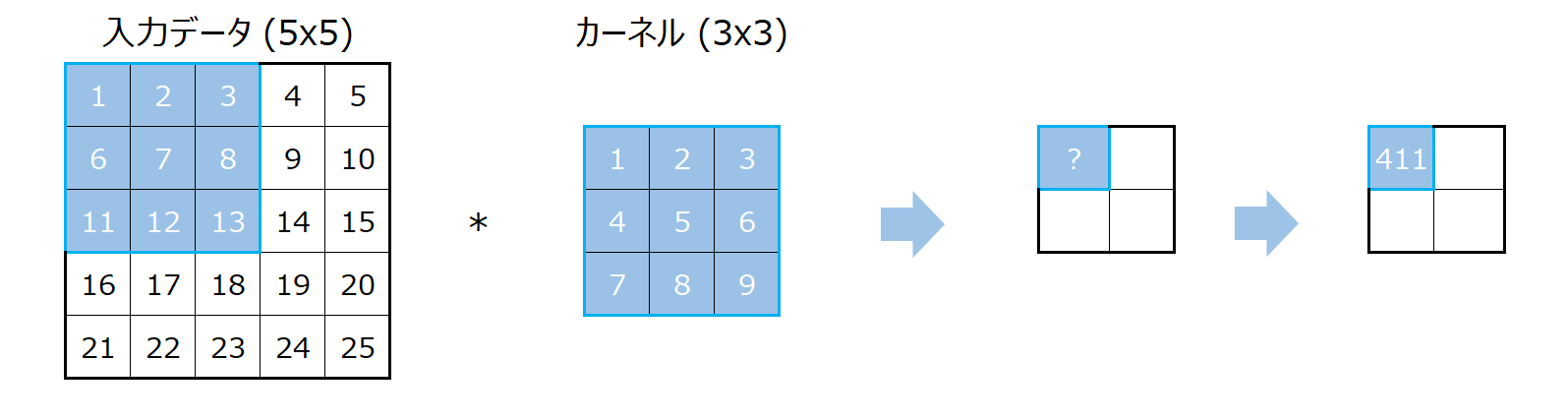
まず、入力データの左上からカーネルと同じサイズを取ってきます。
このエリアとカーネルを使って計算することで、アウトプットの左上が求まります。
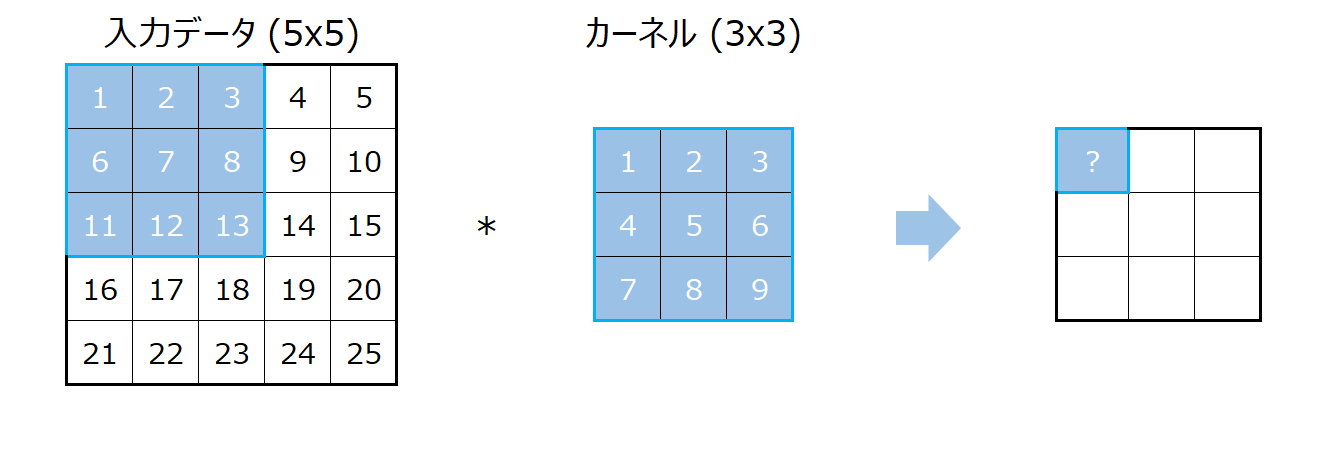
どのように計算するかというと、入力の3x3のエリアとカーネルは同じサイズなので、同じ場所にある要素同士を掛け算し、その結果を合計します。
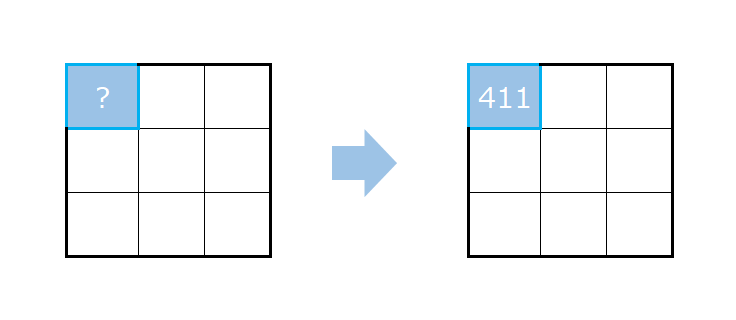
上記の場合だと、
$$1\times 1 + 2\times 2 +3\times 3 +4\times 4 +5\times 5 +6\times 6 + 7\times 7 +8\times 8 + 9\times 9 =411$$
となります。
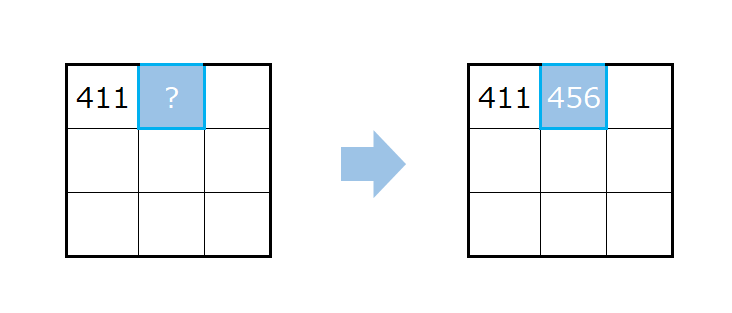
つづいて、入力のエリアを右に一つずらした部分を抜き出し、その部分とカーネルを同じように掛け算します。
そして、その結果はアウトプットの右に一つずらした箇所に対応します。
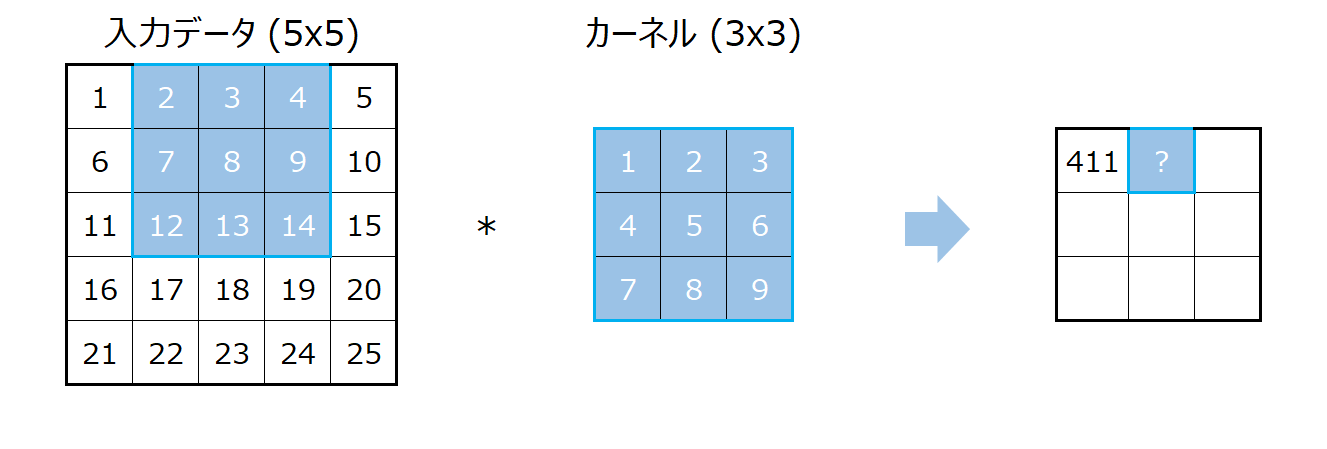
計算方法も同じで、同じ場所にある要素同士を掛け算し、その結果を合計します。
ここでは、
$$2\times 1 + 3\times 2 +4\times 3 +7\times 4 +8\times 5 +9\times 6 + 12\times 7 +13\times 8 + 14\times 9 =456$$
となります。
次も同じで、もう一つ右にずらすだけです。
計算方法は全く同じです。
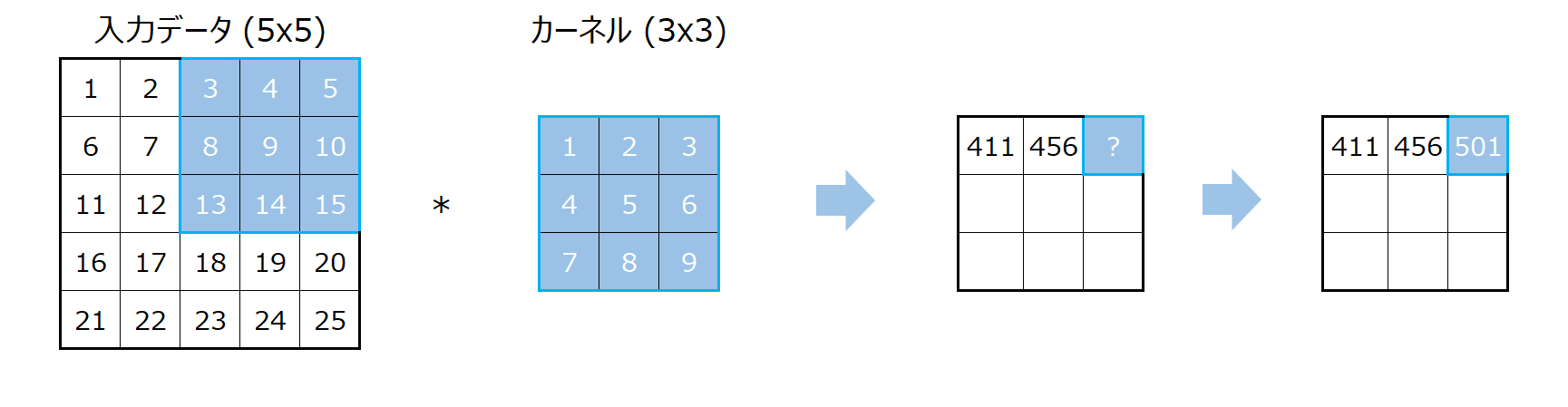
ここまで計算するとわかりますが、これ以上右にずらすことはできないので、5x5のインプットデータに3x3のカーネルを適用すると横は3列にしかなりません。
続いて、一番左から一つ下に下がります。
こちらも計算方法は全く同じです。
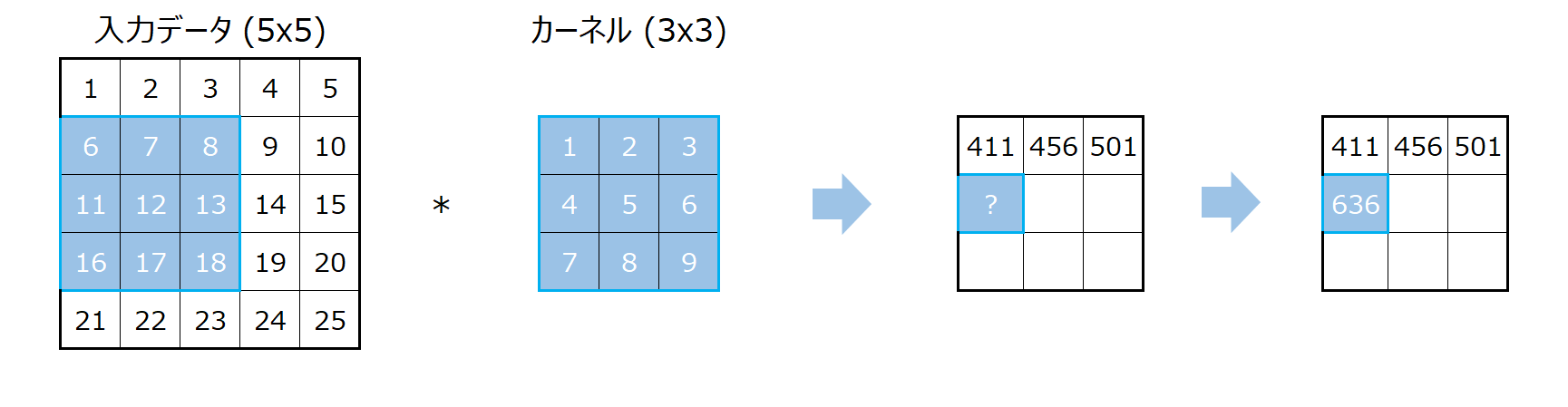
これを続けることで最終的な計算結果は以下になります。
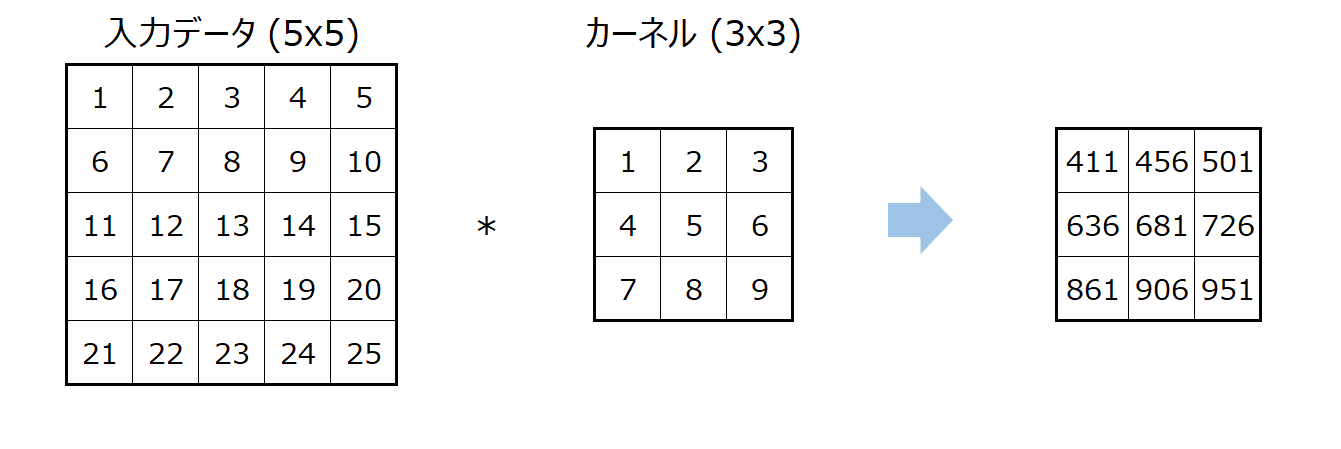
この場合はバイアス項がありませんでしたが、バイアス項を使う場合は、各アウトプットにバイアスが足されます。
$$X*filter+bias$$
これが基本的な畳み込みの計算方法です。
複数チャネルの畳み込み
今まで見たのは2次元の畳み込み処理でしたが、複数のチャネルを持つ畳み込み処理が一般的です。
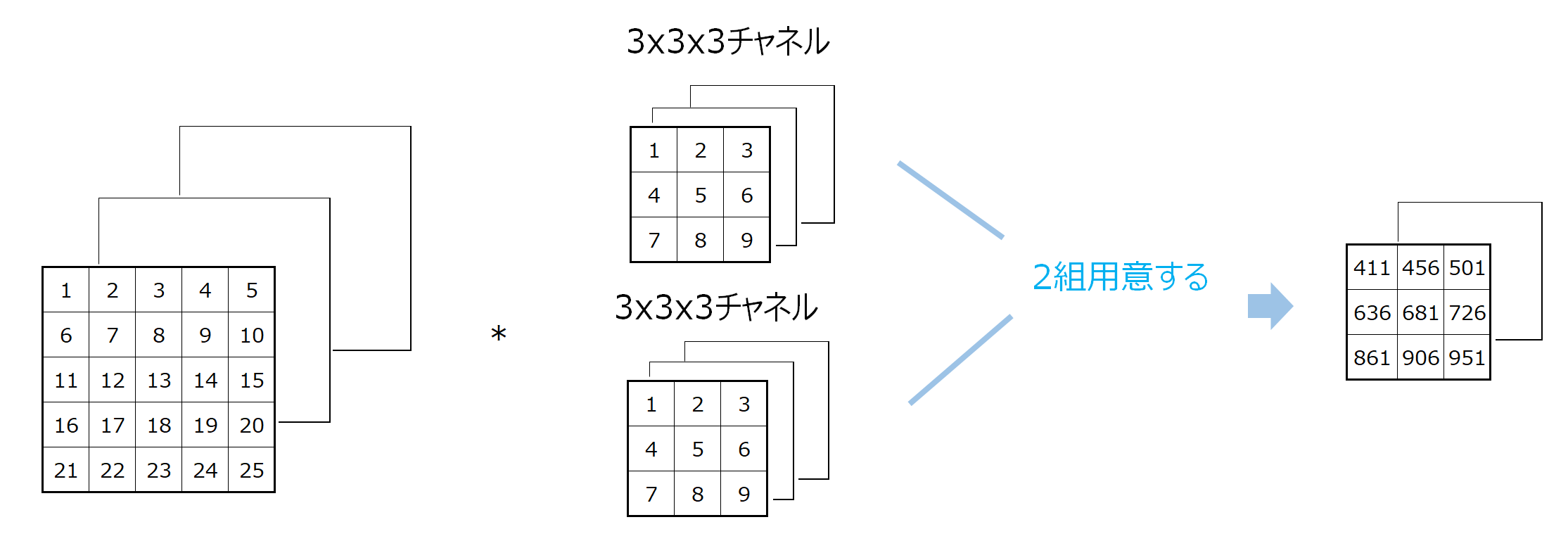
例えば、RGB画像のようなチャネル数が3の場合を考えてみましょう。
この場合は、3x3のカーネルをインプット・チャネルの数分(この場合は3つ)用意します。
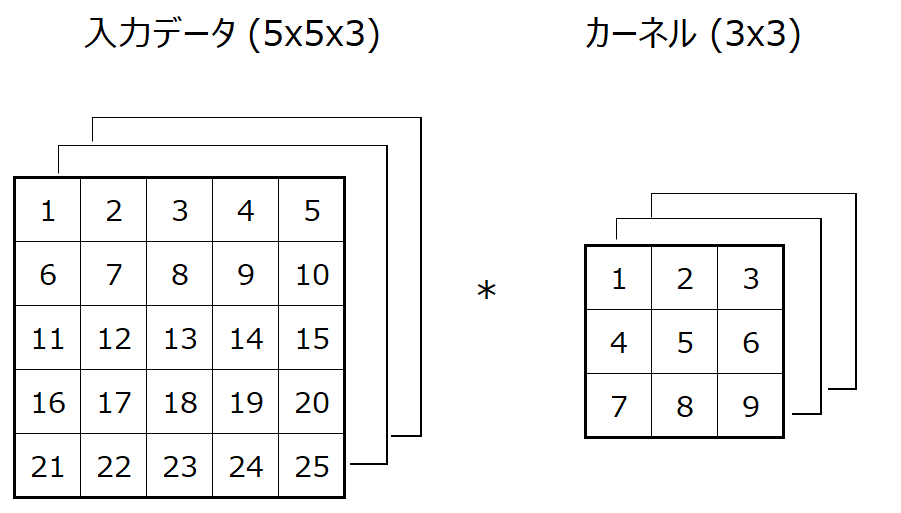
この場合だと3x3x3なので27個のパラメータになります。
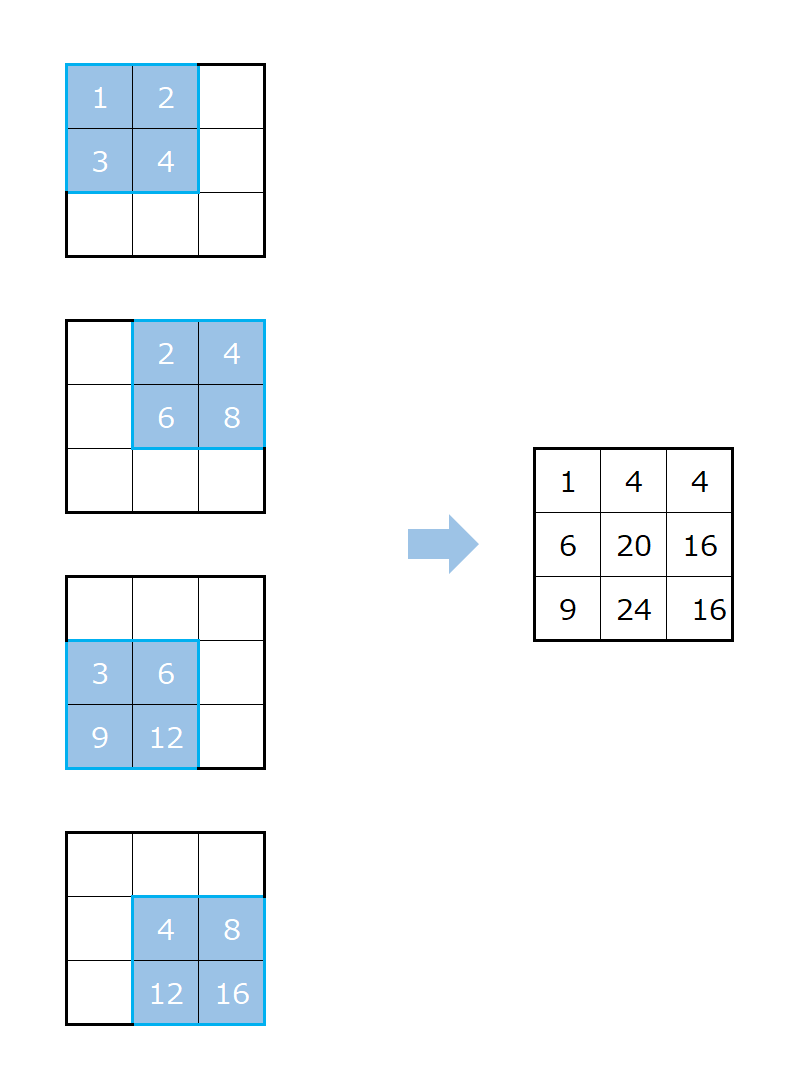
そして、チャネルごとに畳み込み演算を行います。
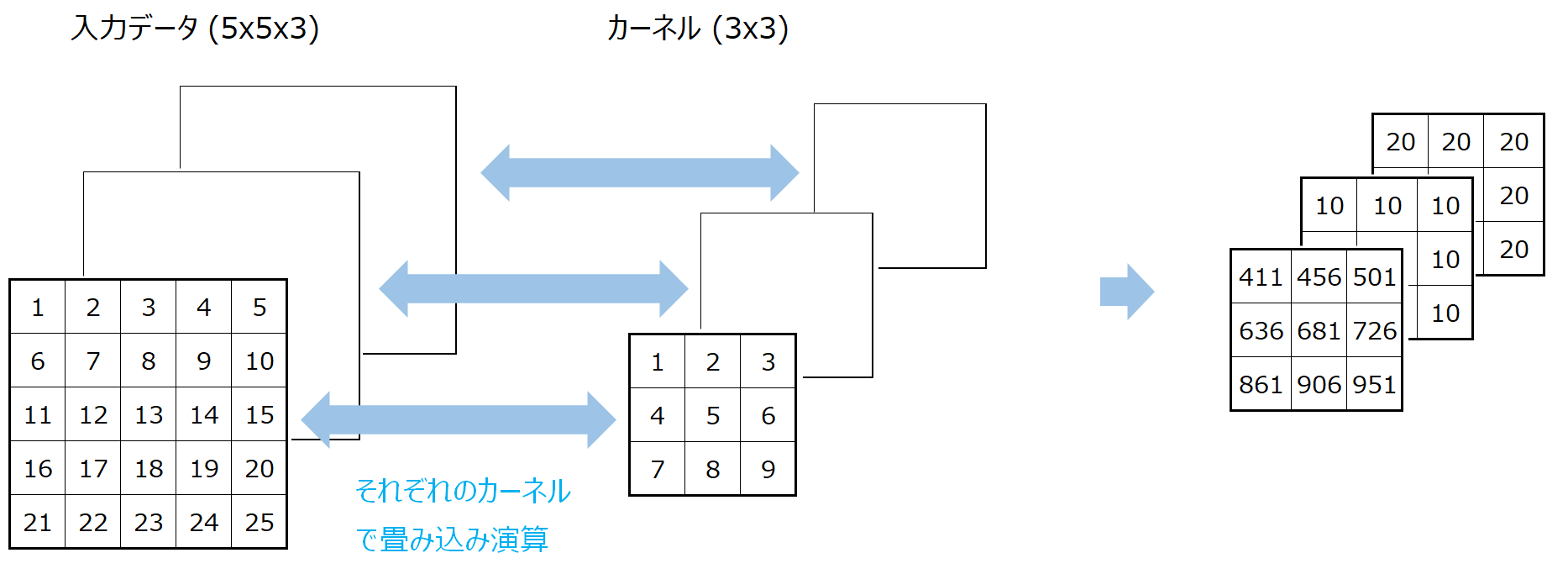
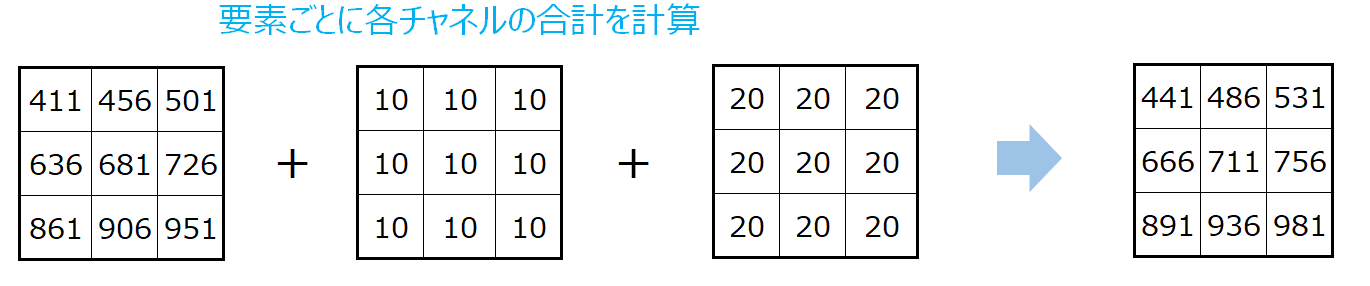
そして、最後に要素の位置ごとに各チャネルの値を合計します。
一番左上だと、411+10+20=44となります。
これで3チャネルのインプットに1つのカーネルを使って畳み込み演算をすることができました。
続いて、3チャネルのインプットデータを畳み込み演算で5チャネルにするなど、アウトプットのチャネルを増やしていくような場合です。
CNNによる分類などでは、インプットはRGB画像だと3チャネルでスタートしますが、これを畳み込み処理で32チャネル、64チャネルと増やしていくことが一般的です。
この場合は、さらにカーネルを増やします。
簡単な例として、1チャネルのインプットデータを3つのチャネルにする場合は、カーネルを3つ用意し、それぞれに畳み込み演算を行います。
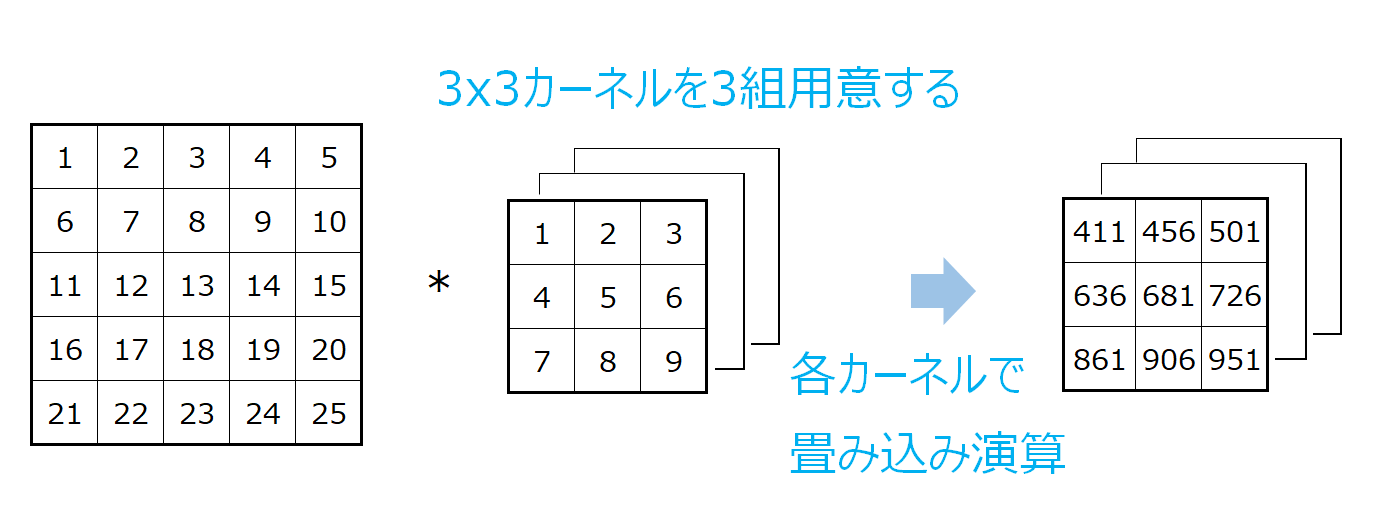
これでアウトプットが3x3x3(チャネル)となりました。
\(C_\text{in}\)チャネルのインプットデータを出力がさらに\(C_\text{out}\)チャネルにする場合は、\(C_\text{in}\)個ののカーネルを\(C_\text{out}\)組用意して、同じように畳み込み処理をします。
アウトプットのサイズ
では、アウトプットのサイズがどのようになるかを見ていきましょう。
5x5の入力データに3x3のカーネルを適用すると3x3のアウトプットになりました。
では、このサイズの計算を一般化しましょう。
インプットの横方向のサイズを\(W\)とし、カーネルサイズを\(K\)とします。
この場合、\(W\)と\(K\)が同じ場合、一つのアウトプットしか計算されないので、アウトプットのサイズは1になります。
\(W\)が1増えるとアウトプットのサイズは1増え、\(K\)が1増えるとアウトプットのサイズは1減ります。
以上より、インプットサイズ\(W\)(横幅のみ)、カーネルサイズ\(K\)の場合のアウトプットのサイズは
$$W-K+1$$
となります。
縦方向も同じ考え方ができるので、入力データのサイズが\(H\times W\)、カーネルサイズが\(K\)の場合アウトプットのサイズは
$$(H-K+1)\times (W-K+1)$$
となります。
先ほどの例だと5x5の入力データに3x3のカーネルを適用しているで、アウトプットは
$$(5-3+1)\times (5-3+1) =3\times 3$$
となっています。
このようにカーネルのサイズが2以上であればアウトプットのサイズは小さくなりますが、これは各エリアの情報を凝縮していると考えられます。
パディング
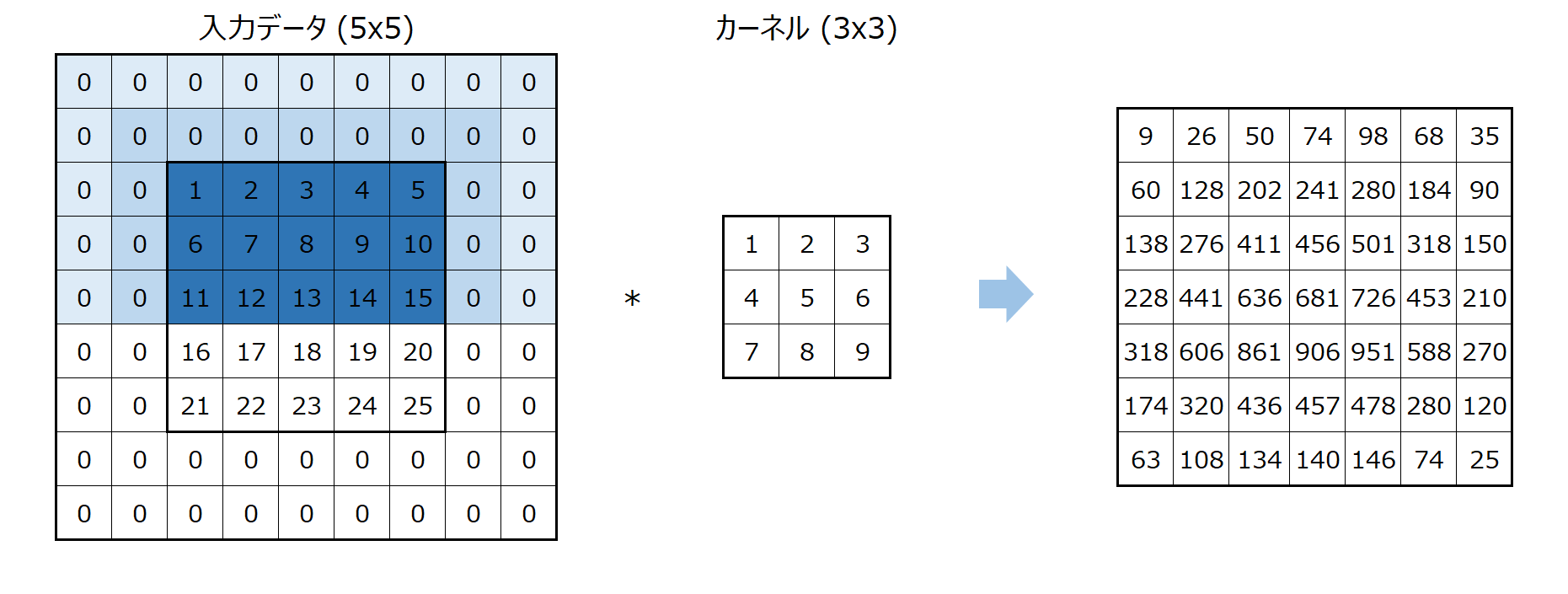
畳み込み演算をよく見ると、入力の中央は何回も計算に使われていますが、一番端の列や一番端の行は使われる回数が少なく、特に角になると1度しか計算に使われません。
以下の図のように、列方向にだけカーネルを適用した場合でも(わかりやすさのために列方向だけにしています)、濃い青の箇所は多く演算に使われ、薄い部分は演算が少なくなります。
画像処理においては、こういった端や角の部分が重要になる場合も多いです。
そこでパディングと呼ばれる処理を使います。
処理は非常に単純で入力データの周りに0の行、列を設定するだけです。
これにより、入力データの端の部分も同じ回数使われるようになります。
パディングをした場合のアウトプットのサイズ
アウトプットのサイズについては、単純にインプットのサイズがパディング数×2だけ大きくなるので、パディングを\(p\)とすると、
$$(H+p\times 2-K+1)\times (W+p\times 2-K+1)$$
となります。
ですので、カーネルサイズの半分だけ両端にパディングすると、アウトプットの出力のサイズがインプットのサイズと同じになります。
ストライド
ストライドはカーネルをずらす幅を意味します。
今までの例ではストライドを1としていたので、カーネルを1つずずらしていました。
ストライドを2以上にすると、これを複数ずらすようにします。
例えば、5x5のインプットに3x3のカーネルをストライドが2で適用します。
この場合、左上の計算は同じです。
その次は右に2つずらします。
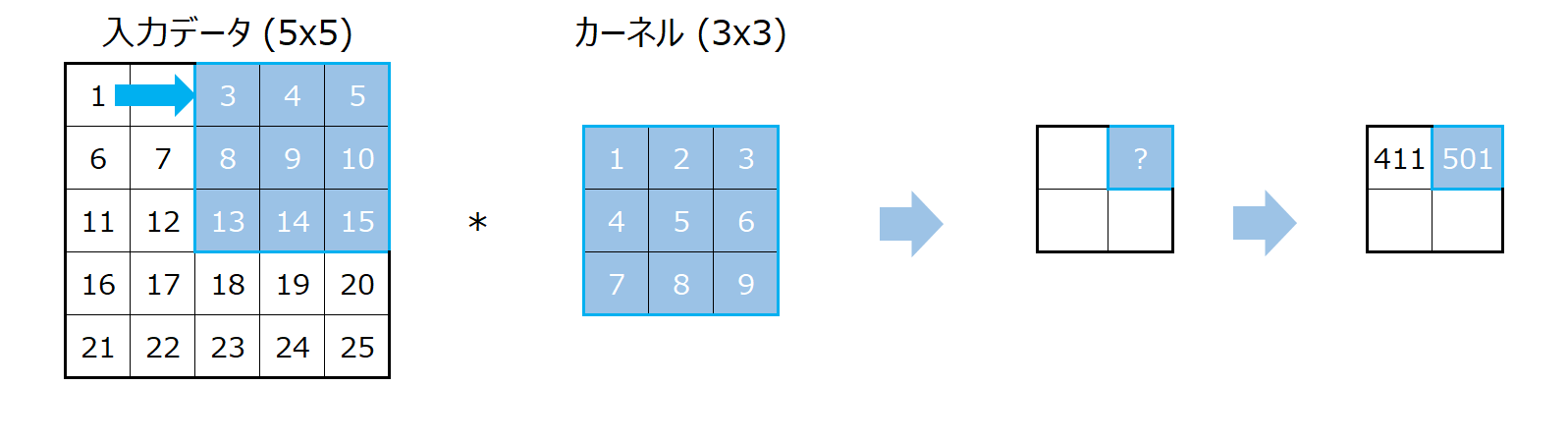
下にずらす場合も2つずつずらすことになります。
これにより、サイズが少し小さくなります。
カーネルサイズを大きくしてもアウトプットのサイズは小さくなりますが、その分計算量も増えます。
ストライドを増やすことによって、計算量を増やさずに情報を凝縮することができると考えられます。
その分、処理は粗くなってしまうので、計算量とのトレードオフになります。
ストライドを変えた場合のアウトプットのサイズ
少しややこしいですが、ストライドを2倍にすると2倍横に動かすことになるので、アウトプットのサイズが半分になります。
ですので、これを一般化するとアウトプットサイズは
$$\left(\frac{W+p\times 2-K}{s}+1\right)\times \left(\frac{H+p\times 2-K}{s}+1\right)$$
になります。
厳密には割り切れない場合があるので、整数に丸めてやる(繰り下げる)ことになります。
Max PoolingとAverage Pooling
続いてプーリングと呼ばれる処理です。
これは情報を凝縮し、データのサイズを小さくします。
名前は難しそうですが、計算方法はいたってシンプルです。
5x5のインプットに3x3のMax Pooling(最大値プーリング)を適用する場合は、畳み込み演算と同様に左上からカーネルと同じサイズのエリアを取ってきます。
そして、そのエリアの最大値を取ってきて、それがアウトプットの一番左上に設定します。
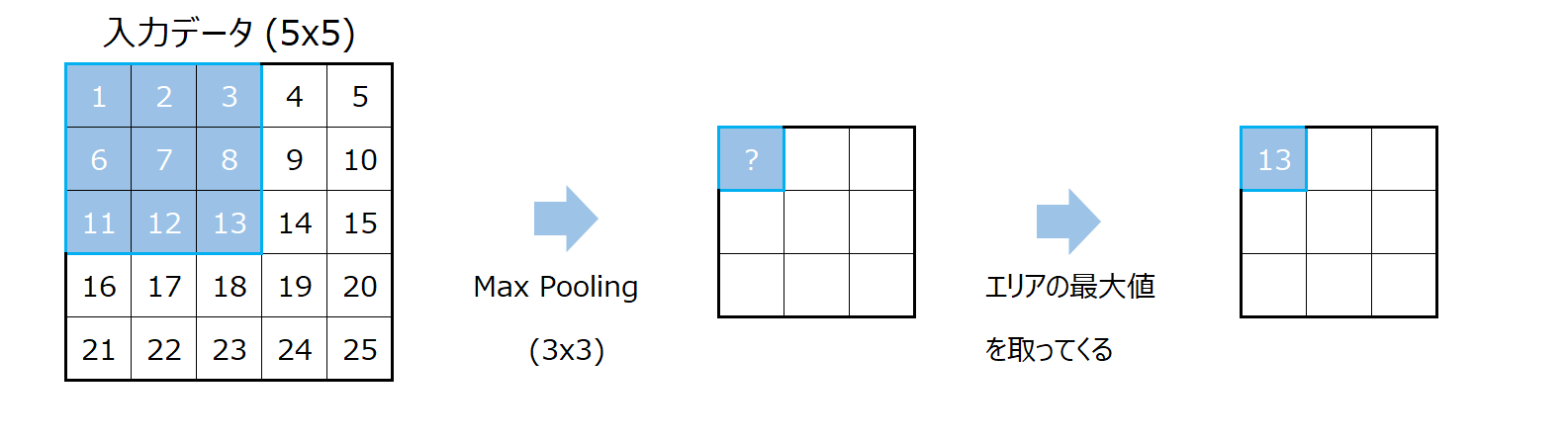
次も畳み込み演算と同様に行います。
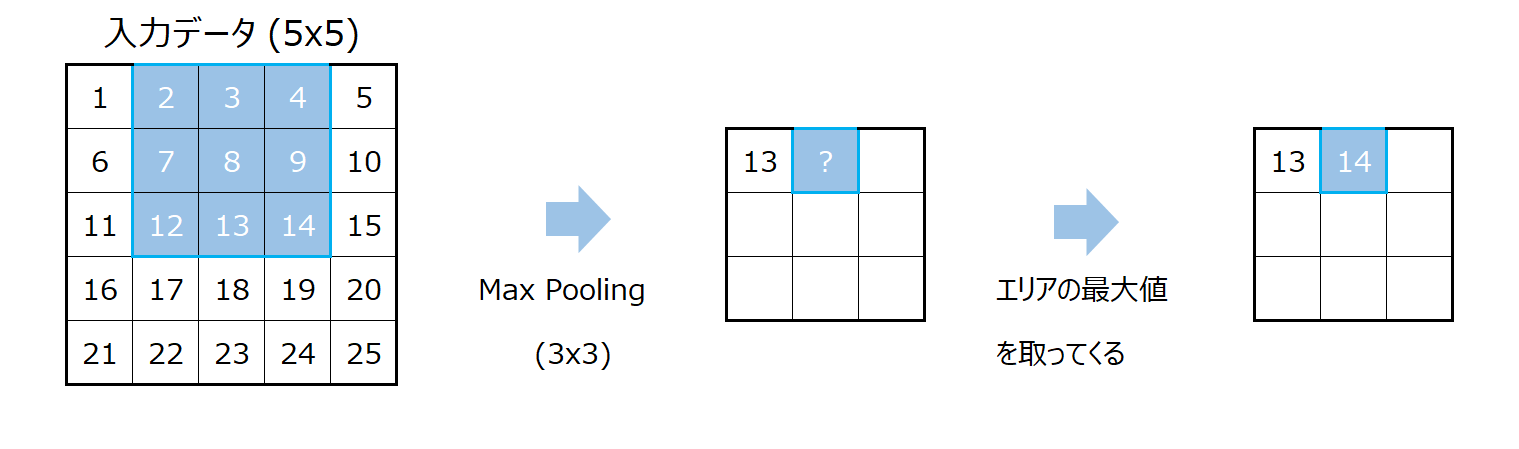
最終的なアウトプットはこのようになります。
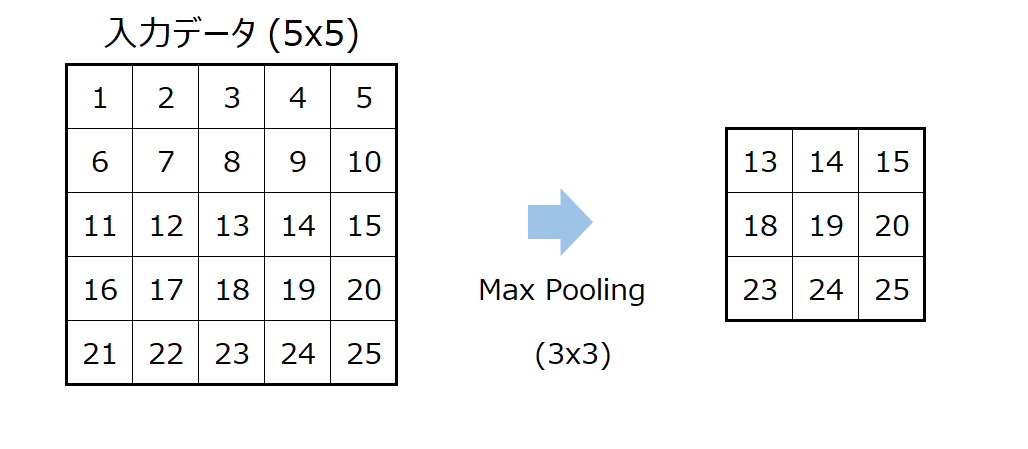
Average Pooling(平均値プーリング)もMax Poolingと同じ考えです。
Average Poolingでは最大値の代わりにエリアの平均値を使います。
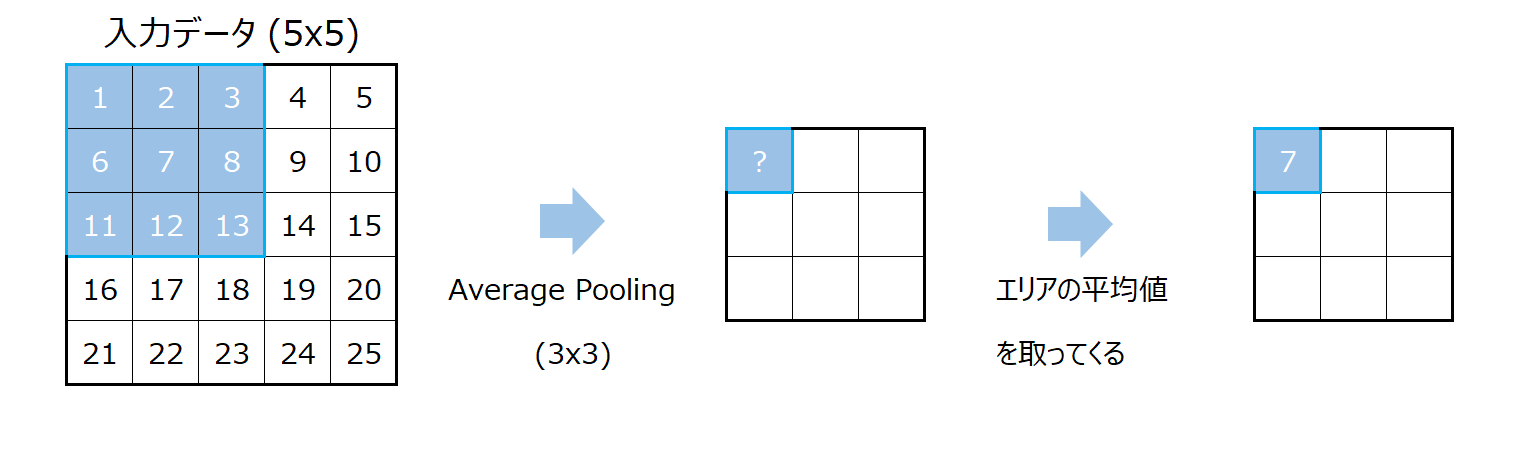
これをすべてのエリアに対して行うことで以下のような結果が得られます。

アウトプットのサイズ
Max PoolingとAverage Poolingによる出力次元についても、畳み込み演算と同様の考え方で、
$$(H-K+1)\times (W-K+1)$$
となります。
Poolingの意味
Pooling処理にはパラメータがないので、この処理自体は何も学習しません。
しかしながら、アウトプットは次元が小さくなりました。
つまり、サイズを落とす効果があります。
これをダウンサンプリングと呼びます。
その際の落とし方として、エリアの平均的や最大値が使われていますが、これはエリアの平均値がそのエリアの重要な特徴を表していると考えるか、エリアの最大値が重要な特徴を表していると考えるかの違いです。
いずれにせよエリアの特徴だけに焦点を当てることでサイズを落とすという効果があります。
転置畳み込み演算
転置畳み込みは畳み込み演算とは逆の演算で、主にサンプルサイズを大きくしたい場合に使います。
これをアップサンプリングと呼びます。
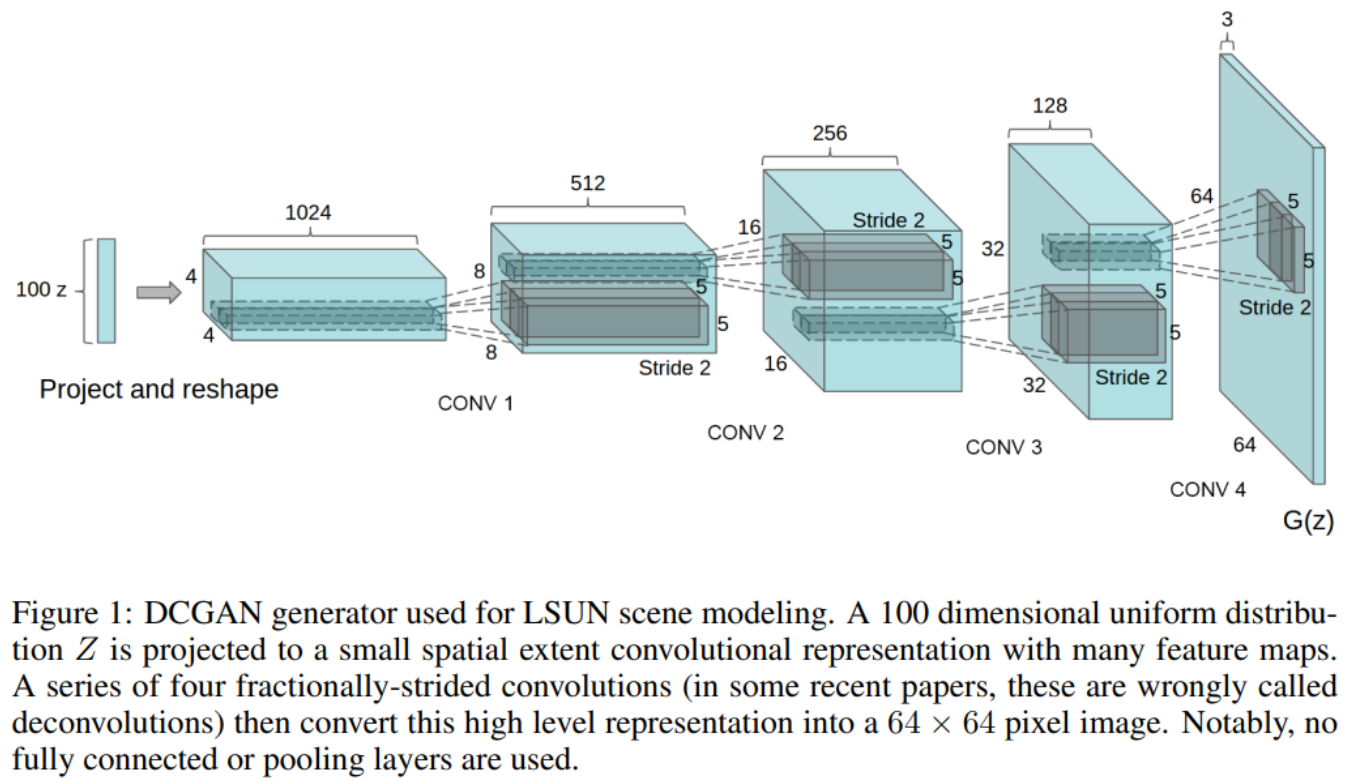
GANでは1024x1024の画像を生成するのに、例えば1次元のノイズベクトルからスタートします。
これを徐々にに大きな画像サイズにしていきます。
DCGANでは4(高さ)x4(幅)x1024(チャネル)を徐々に大きなサイズにしていき、最終的に64x64x3(RGB)などにしていきます。
計算方法も畳み込み処理と同じようにシンプルです。
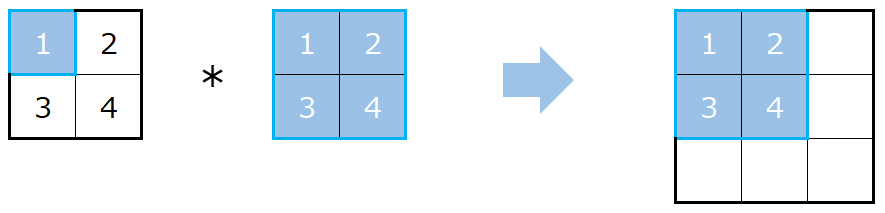
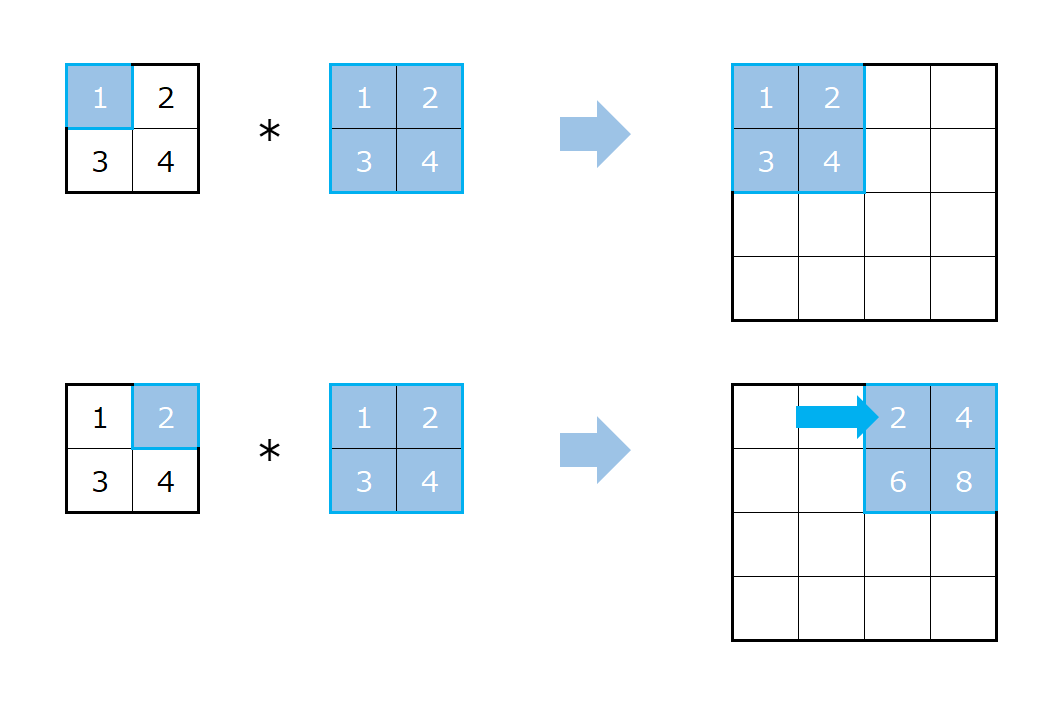
2x2のインプットに2x2のカーネルを使って転置畳み込みをする場合を考えます。
この場合は、インプットからまず左上の一つだけを取り出します。
そして、カーネルの各要素と掛け算をし、それをアウトプットの左端に並べます。
つづいてインプットを一つ右にずらします。
同様にその部分とカーネルを掛け算し、その結果をアウトプットの右に一つずらした場所に設定します。
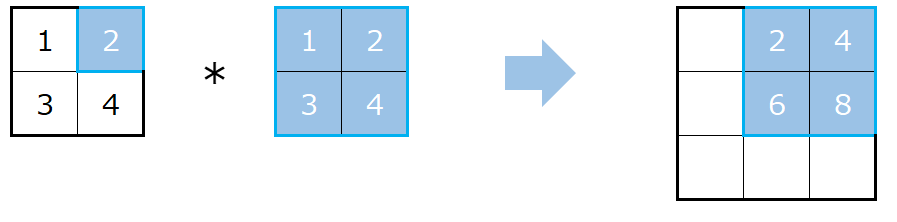
これにより、アウトプットのサイズは3になります。
同様に、左下、右下と計算していきます。
最後に上記で計算された各数値を位置ごとに合計します。
以上が転置畳み込みの基本的な計算方法です。
ここでは、1つのチャネルが入力でアウトプットも1チャネルでしたが、複数のチャネルがある場合、複数のチャネルをアウトプットとする場合についても通常の畳み込みと同様で複数の転置畳み込みカーネルを用意することで可能です。
ストライドとパディング
ストライドについても、考え方は通常の畳み込みと同じで、縦横にずらす間隔を指定します。
上記の例はストライドが1の場合でしたが、ストライドが2の場合は縦横に2ずつずらします。
パディングも同様でインプットデータの周りにゼロを設定します。
ただし、PyTorchではdilationというパラメータとカーネルのサイズを使って、以下の式で実際に入力データにパディングする数を決定します。
$$\text{実際のパディング} = dilation * (kernel\_size - 1) -padding$$
これは畳み込み処理と転置畳み込み処理を逆関係にするためのもので、padding=1と設定しても入力データの両端に1列・1行ずつ追加されるわけではないのでご注意ください。
アウトプットのサイズ
転置畳み込みの出力サイズは、インプットの幅を\(W\)、カーネルサイズを\(K\)とすると、インプットのの1つの位置に対してサイズ\(K\)のアウトプットとなり、それを1つずつ動かして合計で\(W-1\)動かすことになるので、
$$W+K-1$$
となります。
高さについても同様なので、最終的に
$$(W+K-1)\times(H+K-1)$$
がアウトプットになります。
パディングは畳み込みと逆の操作を行うので、
$$(W-1-p\times 2+K)\times(H-p\times 2+K)$$
となります。
ストライドを使うとストライド分だけ大きく動かすのでインプットが\(s\)倍されたのと同じになり、最終的に以下のようになります。
$$((W-1)\times s-p\times 2+K)\times ((H-1)\times s-p\times 2+K)$$
まとめ
今回は畳み込み処理と転置畳み込み処理について見てきました。
実際にPyTrochやTensorflowで試してみると理解が深まるかと思います。
もちろんExcelなどで実際に計算してみるのも良いと思います。
では!