前回はDiffusionモデルのコアの仕組みであるforward process、reverse process、損失関数を実装しました。
Diffusionモデル自体はニューラルネットワークのモデルを表しているのではなく、ニューラルネットワークはどこで出てくるかというとreverse processで出てくるパラメータ\(\mu_\theta\)もしくは\(\epsilon_\theta\)を求めるところです。
ということで今回は、\(\mu_\theta\)もしくは\(\epsilon_\theta\)を求めるニューラルネットワーク、U-Netについて実装したいと思います。
U-Netの原論文はこちらですので興味がある方は読んでみてください。
『U-Net: Convolutional Networks for Biomedical Image Segmentation』
Diffusionモデルについては、以下の記事で細かく解説しています。
また、今回もHuggin Faceの実装を参考にしています。
『The Annotated Diffusion Model』
目次
U-Netとは
U-Netはもともと医療用の画像のセグメンテーションのためのモデルとして2015年に提案されたモデルです。
モデルの仕組みが以下のようにU字の形をするためU-Netと名付けられています。
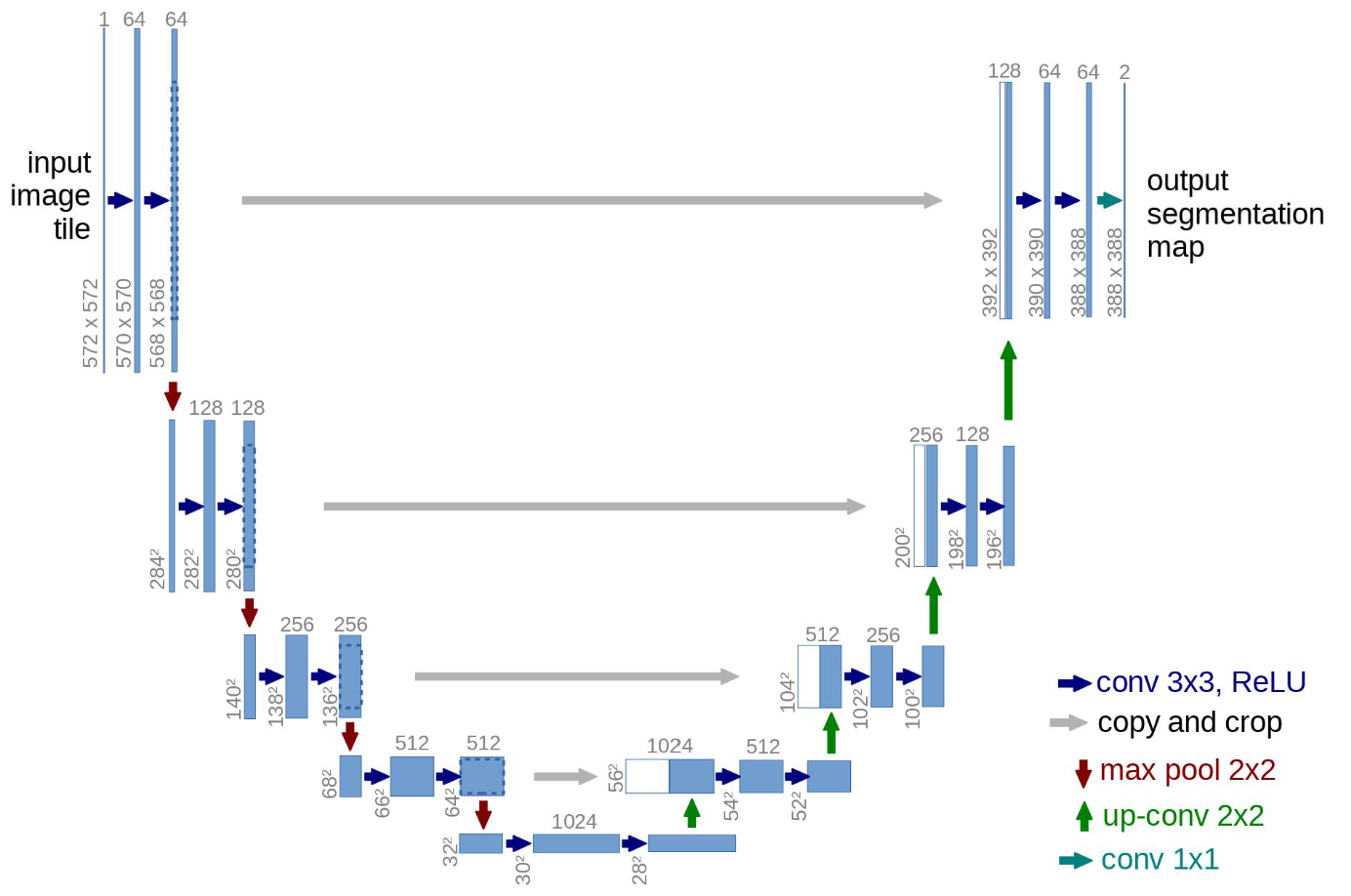
この図の仕組みを簡単に説明すると、まず図の左側の部分でインプット画像をダウンサンプルしていきます。
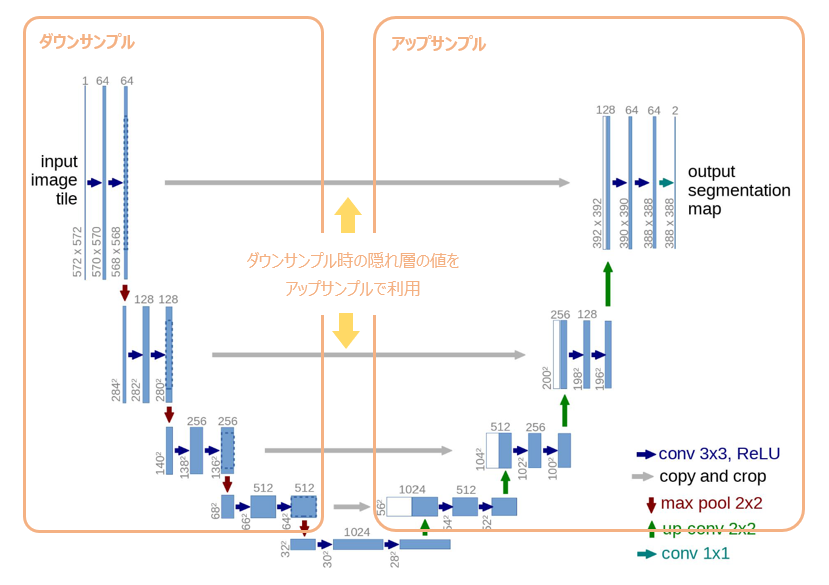
ダウンサンプルというのは、畳み込み処理を使って画像のサイズを圧縮しながら、チャネル数を増やしていくものです。
上記では、572x572x1の画像を28x28x1024に圧縮しています。
そして、右側の部分で画像をアップサンプルしていきます。
アップサンプルというのはダウンサンプルとは逆で、転置畳み込み処理を使ってダウンサンプルされた画像を大きくしていくものです。
畳み込み処理、転地畳み込み処理って何?という方はこちらをご参照ください。
そしてポイントは、アップサンプルする際に、図の灰色の横矢印のようにダウンサンプル時の隠れ層の値をアップサンプル時の隠れ層の値に結合している点です。
これにより、ダウンサンプル時の情報をアップサンプル時に利用することができるというものです。
DiffusionモデルにおけるU-Net
今回作成するU-Netの全体像はこのような形をしています。
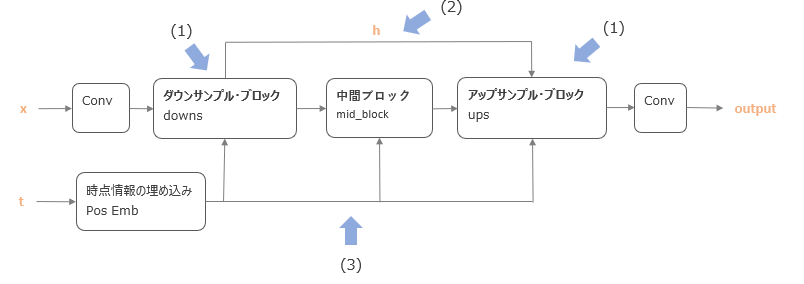
考え方はオリジナルのU-Netと同じですが、ポイントは以下です。
- ダウンサンプルして、その後アップサンプルを行う。
- ダウンサンプルの際の隠れ層の値をアップサンプル時に利用する。(上矢印のh)
- 時点情報の埋め込み表現を計算し、各ブロックに付加する。(下段のPos Emb)
1番目と2番目はオリジナルのU-Nettお同じで、3番目の時点情報の埋め込み表現を使う点はDiffusionモデル独特の部分です。
オリジナルのU-Netとの違い
若干、上述の内容と重複しますが、Diffusionモデルでは通常のU-Netをさらに改良していおり、具体的には以下の違いがあります。
- 時点情報(Position embeddings)の付加
\(\epsilon_\theta({\bf{x}}_t, t)\)はパラメータが\(\theta\)となっているように時点によらず同じパラメータを使用します(\(\theta_t\)とはなっていない)。
しかしながら、インプットパラメータに\(t\)がある通り、モデルはどの時点かを知る必要があります。
そこで、Transformerで提案されたような時点の情報を表す埋め込み表現を導入します。 - Wide ResNetの利用
論文ではResNetブロックにWide ResNetが使われています。
Hugging FaceのブログではConvNeXTブロックが実装されており、そちらが使用されていますので、興味のある方はHugging Faceのブログの実装を参照していただければと思います。
ただ、今回の実装では簡単にするため通常のResNetを使用します。 - Attentionの導入
現在では自然言語処理だけではなく画像分野でもAttentionメカニズムは非常によく使われていますが、ここではTransformerで使われているdot-porduct attention、およびlinear attentionを導入します。 - Group Normalizationの導入
バッチ正規化ではなくグループ正規化(Group Normalization)(『Group Normalization(グループ正規化)を理解する』をご参照)を使います。
以上がオリジナルのU-NetとDiffusionモデルで実装しているU-Netの違いです。
では、順番に実装しながら見ていきましょう。
Diffusionモデル版U-Netの実装
前準備をしておきます。
まずはモジュールのインポートです。
import math # positional embeddingsのsin, cos用 from inspect import isfunction # inspectモジュール from functools import partial # 関数の引数を一部設定できる便利ツール # PyTorch, 計算関係 import torch from torch import nn, einsum import torch.nn.functional as F from einops import rearrange
続いて補助関数を作成します。
引数xがNoneでなければTrueを返し、NoneであればFalseを返す関数を作成します。
def exists(x): return x is not None
また、1つめの引数valがNoneでなければvalを返し、valがNoneであれば2つ目の引数dを返す関数を作成します。
def default(val, d):
"""
valがNoneでなければTrueを返す.
Noneの場合, dが関数であれば関数を呼び出した結果を返し, 関数でなければその値を返す.
"""
if exists(val):
return val
return d() if isfunction(d) else d
では、メインとなる仕組みを見ていきましょう。
時点情報の埋め込み表現(Position Embeddings)
まずは時点情報の埋め込みです。
Diffusionモデルでは各時点\(t\)ごとにノイズを予測しますが、どの時点でもニューラルネットワークの重みは同じです。
つまり、時点\(t\)ごとにモデルを作成するわけではありません。
しかし、どの時点か?という情報がある方が、ノイズを予測しやすくなります。
そこで、モデルに時点\(t\)に対応する情報を入れることを考えます。
Diffusionモデルでは、Transformerで提案されたPosition Embeddingsという考え方を利用します。
(Transformer, Position Embeddingsについてはこちらをご参照ください 『【論文解説】Transformerを理解する』)
Transformerではsin関数、cos関数を使って以下の式で表されます。
\begin{align}
P E_{(pos,2i)} &= sin(pos/10000^{2i/d_{model}}) \tag{1}\\
P E_{(pos,2i+1)} &= cos(pos/10000^{2i/d_{model}}) \tag{2}
\end{align}
ここでは\(pos\)が時点を表し、\(i\)が次元を表します。
class SinusoidalPositionEmbeddings(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, time):
device = time.device
half_dim = self.dim // 2 # 次元の半分
embeddings = math.log(10000) / (half_dim - 1)
embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
embeddings = time[:, None] * embeddings[None, :]
embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
return embeddings
以下で、\(1/10000^{2i/d_{model}}\)の部分を計算しています。
8行目で対数を取っていますが、9行目でexponentialを取っています。
half_dim = self.dim // 2 # 次元の半分 embeddings = math.log(10000) / (half_dim - 1) embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
続いて、こちらで\(pos/10000^{2i/d_{model}}\)を計算しています。
embeddings = time[:, None] * embeddings[None, :]
最後にsin、cosを取って結合しています。
embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
では、表示して確認しましょう。
時点を1000までとし、次元を500とします。
import matplotlib.pyplot as plt
timesteps = 1000
time = torch.arange(timesteps)
pos_emb = SinusoidalPositionEmbeddings(dim=500)
emb = pos_emb(time=time)
plt.pcolormesh(emb.T, cmap='RdBu')
plt.ylabel('dimension')
plt.xlabel('time step')
plt.colorbar()
plt.show()
すると以下のように時点、次元によって[-1, 1]のある程度異なる値が設定されているのがわかります。
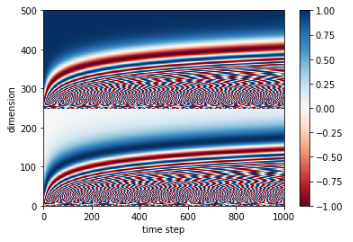
このPosition Embeddingを隠れ層の値に足すことで、隠れ層の値に時点情報を入れることができます。
ちなみに、上記の実装ですが、そのまま結合しているだけなので\((1)\)式、\((2)\)式とは若干違いますね。
このような感じで実装されているように思えます。
\begin{align}
P E_{(pos,i)} &= sin(pos/10000^{2i/d_{model}}) \text{ if }i \le d_{model} / 2 \\
P E_{(pos,i)} &= cos(pos/10000^{2i/d_{model}}) \text{ if }i > d_{model} / 2
\end{align}
(違ったらご連絡ください...)
ニューラル・ネットワークのための補助クラス
では、本体のネットワーク部分を作成していきますが、まずそこで使う補助クラスを作成しておきます。
残差結合(Residual)
残差結合を使うので、まずは残差結合のクラスを作成しておきます。
単純に\(f({\bf{x}})+{\bf{x}}\)を実装しています。
class Residual(nn.Module):
"""
残差結合
"""
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, *args, **kwargs):
"""
f(x) + x
"""
return self.fn(x, *args, **kwargs) + x
アップサンプル(Upsample)用の畳み込み層
また、アップサンプル用、ダウンサンプル用のクラスも作成しておきます。
アップサンプルは転置畳み込み処理を使います。
カーネルサイズは4、ストライドは2、パディングは1です。
class UpsampleConv(nn.Module):
"""
upsample用Transposed Convolution
"""
def __init__(self, dim):
super().__init__()
self.trans_conv = nn.ConvTranspose2d(
in_channels=dim,
out_channels=dim,
kernel_size=4,
stride=2,
padding=1
)
def forward(self, x):
return self.trans_conv(x)
ダウンサンプル(Downsample)用の畳み込み層
ダウンサンプルは通常の畳み込み処理です。
アップサンプルと同様にカーネルサイズは4、ストライドは2、パディングは1です。
class DownsampleConv(nn.Module):
"""
Downsample用Convolution
"""
def __init__(self, dim):
super().__init__()
self.conv = nn.Conv2d(
in_channels=dim,
out_channels=dim,
kernel_size=4,
stride=2,
padding=1
)
def forward(self, x):
return self.conv(x)
残差結合ブロック
ここからアップサンプル、ダウンサンプル時にメインで使われる“残差結合ブロック(ResnetBlock)”を作成していきます。
残差結合ブロックは、残差結合を用いた畳み込み処理を行うブロックです。
まずは、残差結合ブロックで使う畳み込み処理部分を作成します。
畳み込みブロック(ConvBlock)
畳み込みブロック(ConvBlock)は以下のように、「畳み込み処理 → 正規化 → 活性化関数」という順で処理を行います。

活性化関数はSiLUを使っています。
SiLUは以下で表されます。
$$\text{SiLU}(x)=x\times \sigma(x)$$
ここで\(\sigma(x)\)はシグモイド関数です。
畳み込みブロック(ConvBlock)をコードで書くとこちらになります。
class ConvBlock(nn.Module):
def __init__(self, dim, dim_out, groups=8):
super().__init__()
self.proj = nn.Conv2d(dim, dim_out, 3, padding=1) # conv
self.norm = nn.GroupNorm(groups, dim_out) # normalization
self.act = nn.SiLU() # activation
def forward(self, x):
x = self.proj(x) # conv
x = self.norm(x) # normalization
x = self.act(x) # activation
return x
残差結合ブロック(ResnetBlock)
では、上記の畳み込みブロック(ConvBlock)を利用して、残差結合ブロック(ResnetBlock)を作成します。
Hugging FaceのブログではConvNeXTBlockというのを使用していますが、ここでは簡単にするため通常のResNetを使いたいと思います。
残差結合ブロック(ResnetBlock)は以下のような形になります。
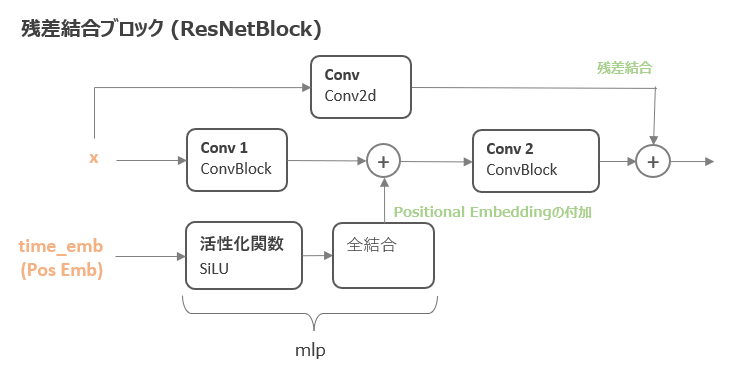
time_embは上記で作成した時点を表すPositional Embeddingで、その情報を画像情報に付加しています。
では、実装してみましょう。
self.mlpが時点を表す情報(time_emb)の処理になります。
class ResnetBlock(nn.Module):
def __init__(self, dim, dim_out, time_emb_dim = None, groups=8):
super().__init__()
# 時点情報(time_emb)
if exists(time_emb_dim):
self.mlp = (
nn.Sequential(
nn.SiLU(),
nn.Linear(time_emb_dim, dim_out)
)
)
else:
self.mlp = (None)
# 画像(x)の処理
self.block1 = ConvBlock(dim, dim_out, groups=groups)
self.block2 = ConvBlock(dim_out, dim_out, groups=groups)
if dim != dim_out: # インプットとアウトプットのサイズが違えばconv
self.res_conv = nn.Conv2d(dim, dim_out, 1)
else:
self.res_conv = nn.Identity()
def forward(self, x, time_emb=None):
# conv1
h = self.block1(x)
# time embの付加
if exists(self.mlp) and exists(time_emb):
time_emb = self.mlp(time_emb)
h = rearrange(time_emb, "b c -> b c 1 1") + h
# conv 2
h = self.block2(h)
# conv + 残差結合
return h + self.res_conv(x)
30行目の以下の処理は、einopsのrearrangeを使って、「バッチサイズ × チャネル数」の2次元の時点の埋め込み情報を「バッチサイズ × チャネル数 × 1 × 1」の4次元に変換しています。
(einopsは適宜インストールしてください)
h = rearrange(time_emb, "b c -> b c 1 1") + h
einopsは行列の次元を交換したりするのに便利なモジュールです。
einopsについてはこちらをご参照ください。(個人的にこのチュートリアル好きです)

Attentionメカニズム
DiffusionモデルのU-NetではAttentionメカニズムを導入しています。
Attentionはもともとは自然言語処理分野で提案されましたが、今や画像分野など様々な分野で欠かすことのできない技術の一つです。
Attentionメカニズムについてはこちらの記事をご参照ください。
⇒ 『Attentionメカニズムを理解する』
ここでは、2種類のattentionを使い分けており、ダウンサンプリング、アップサンプリングの際はlinear attentionを、ダウンサンプリング後の中間ブロックの畳み込み処理には通常のdot-product attentionを使っています。
dot-product attentionについてはこちらをご参照ください
⇒ 『【論文解説】Transformerを理解する』
では、実装していきましょう。
dot-product attention
通常のdot-product attentionのattention weight(「どこに注意を向けるか」を表すウェイト)は、クエリ\(Q\)、キー\(K\)、バリュー\(V\)を使って以下の行列計算で表されます。
\begin{align}
\text{Attention_Weight}=\text{softmax}\left(\frac{QK^T}{\sqrt{d_{\text{model}}}}\right) \tag{3} \\
\end{align}
そして、attention weightとValue \(V\)を掛けて最終的なアウトプットを計算します。
\begin{align}
output =\text{Attention_Weight}\cdot V \tag{4}
\end{align}
通常は、ヘッドを複数に分けたmulti-head attention(マルチ・ヘッド・アテンション)が利用され、multi-head attentionは以下で表されます。
\begin{align}
\text{MultiHead}(Q, K, V) &= \text{Concat}\left(\text{head}_1, \cdots, \text{head}_h\right)W^O \\
\text{where } \text{head} _i &= \text{Attention}\left(QW_i^Q, KW_i^K, VW_i^V\right)
\end{align}
イメージとしては、まず\(Q\)、\(K\)、\(V\)をヘッドの数に分割し、それぞれでattentionを使ってアウトプットを計算し、その後にもとのサイズに結合するものです。
Transformerの論文では、そうする方がうまくいったというのことです。
実装を見た方がわかりやすいと思いますので、まず実装してみましょう。
class Attention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
self.scale = dim_head ** (- 0.5) # d^(-1/2)
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.to_out = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim=1) # Q, K, Vの3つにわける
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q * self.scale
sim = einsum("b h d i, b h d j -> b h i j", q, k)
sim = sim - sim.amax(dim=-1, keepdim=True).detach()
attn = sim.softmax(dim=-1)
out = einsum("b h i j, b h d j -> b h i d", attn ,v)
out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
return self.to_out(out)
処理を一つ一つ見ていきましょう。
まず12行目の処理ですが、こちらはself.to_qkv()で通常の畳み込み演算を行い、chunkメソッドで3つに分けています。
qkv = self.to_qkv(x).chunk(3, dim=1) # Q, K, Vの3つにわける
以下のようなイメージです。
1次元のバッチの次元は除いています。PyTorchに合わせてバッチの次元の次はチャネルの次元にしています。
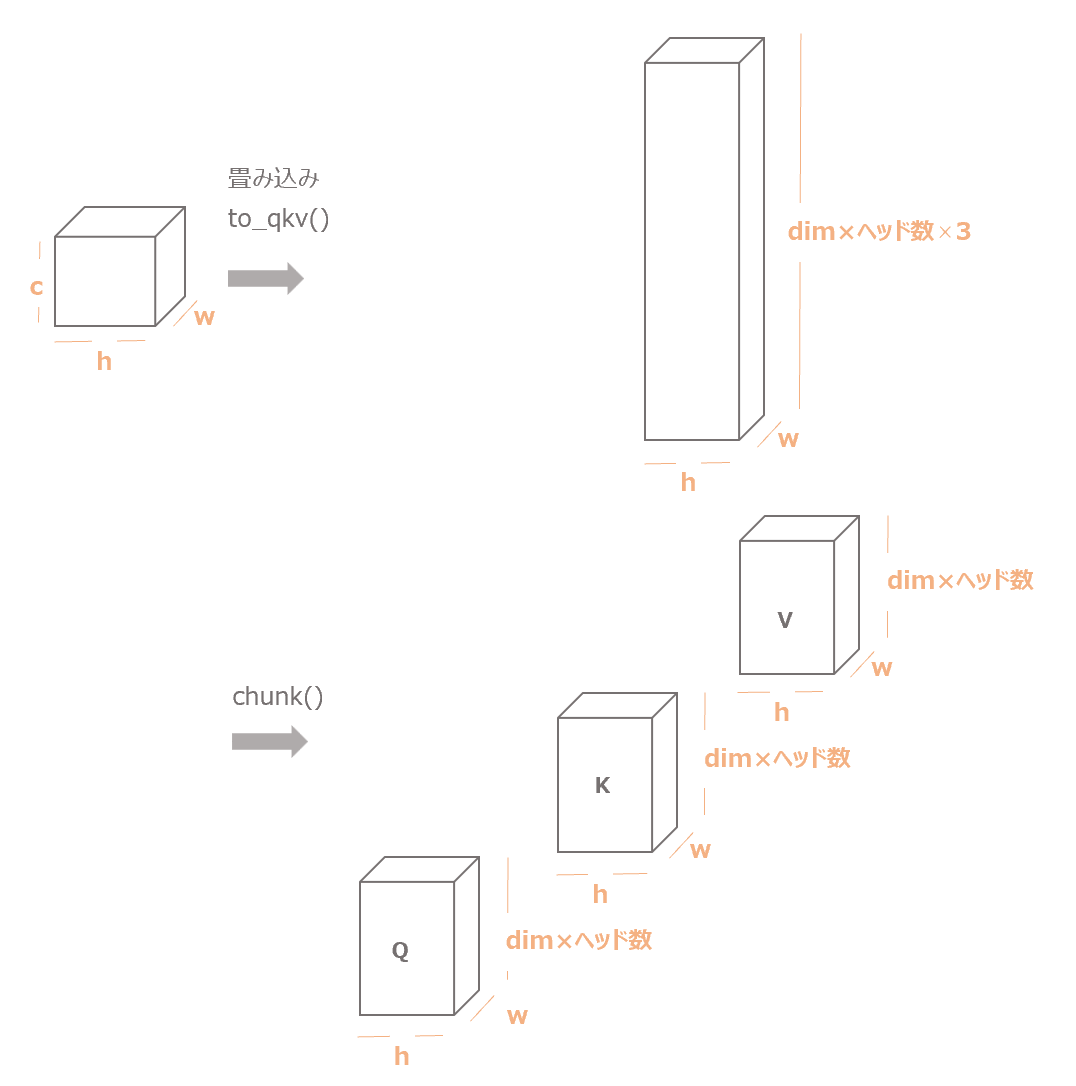
続いて、13行目の処理で形を変形しています。
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
以下の図のように、\((dim \times heads) \times h \times w\)だった行列を\(heads \times dim \times (w\times h)\)に変形しています。
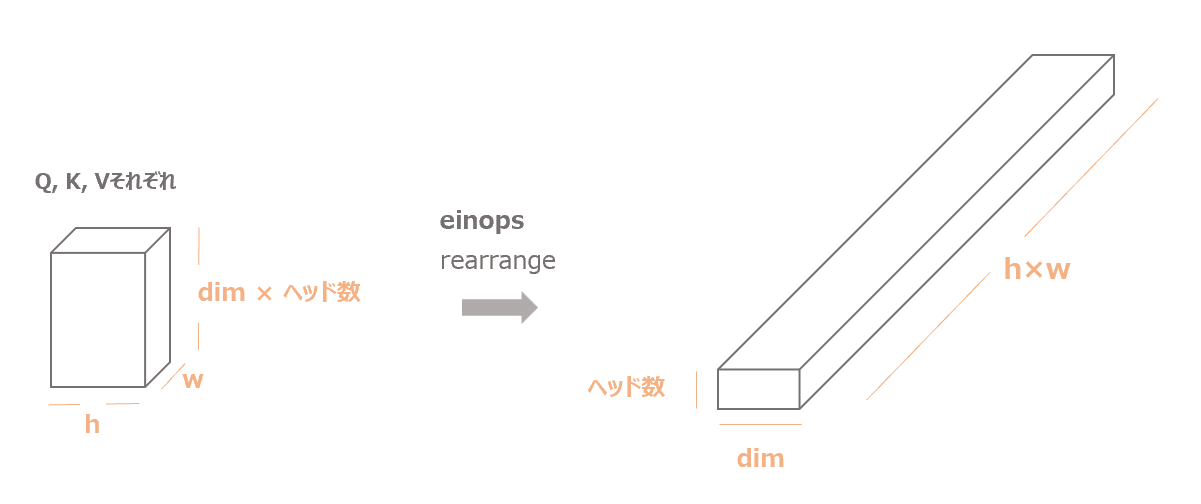
以下は、\(Q/\sqrt{d_\text{model}}\)を計算して、スケーリングしています。
q = q * self.scale
そして、以下の式の通りattentionを計算しています。(softmaxを取る際に計算を安定させる際に最大値を引いています)
\begin{align}
\text{Attention_Weight}=\text{softmax}\left(\frac{QK^T}{\sqrt{d_{\text{model}}}}\right)
\end{align}
sim = einsum("b h d i, b h d j -> b h i j", q, k)
sim = sim - sim.amax(dim=-1, keepdim=True).detach()
attn = sim.softmax(dim=-1)
18行目で行列計算をしていますが、その際にeinsumという関数を使っています。
einsumはPyTorchの関数で行列演算に便利な関数です。『PyTorchのドキュメント』
続いて、attentionとV(value)を掛け合わせてattentionを考慮した出力を計算します。
\begin{align}
Attention=\text{Attention_Weight}\times V
\end{align}
out = einsum("b h i j, b h d j -> b h i d", attn ,v)
out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
最後に畳み込み処理で元の次元(チャネル数)に戻しています。
return self.to_out(out)
以上がdot-product attentionの説明です。
linear attention
では、続いてlinear attentionを実装します。
まず、なぜlinear attentionを使うかについて説明しておきます。
上記のdot-product attentionは\(QK^T\)を計算していますが、この計算はメモリや計算負荷が非常に高くなります。
\(Q\)、\(K\)が\(n\times dim\)だとすると(\(n\)は文章の長さを表します)、出来あがりの行列は\(n\times n\)の行列となります。
例えば、文章の長さが10単語であれば、10×10の100個の要素ですが、1000単語になると1,000,000要素になり、メモリ使用量、計算量が\(O(n^2)\)になることがわかります。
ここが通常のTransformerの欠点と言われており、そのため計算負荷を小さくしたSparse Transformer、Reformer、Longformerなどが提案されています。
今回の画像処理についても同様で、以下の部分で\(i\times dim\)と\(dim\times j\)の行列積をしています。\(i\)、\(j\)は(画像の高さ(h)×幅(w))です。
sim = einsum("b h d i, b h d j -> b h i j", q, k)
ですので、\((h \times w)\)が大きいと非常にメモリ使用量が大きく、計算負荷が高くなります。
このように、\(Q\)、\(K\)の大きさにより計算負荷が非常に高くなってしまうという欠点に対応するためにlinear attentionを使用します。
linear attentionの計算負荷は\(O(n)\)と\(n^2\)ではなく\(n\)に比例する形になります。
linear attentionは以下で実装できます。
class LinearAttention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
self.scale = dim_head ** (- 0.5)
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1),
nn.GroupNorm(1, dim))
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim=1)
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q.softmax(dim=-2)
k = k.softmax(dim=-1)
q = q * self.scale
context = torch.einsum("b h d n, b h e n -> b h d e", k, v)
out = torch.einsum("b h d e, b h d n -> b h e n", context, q)
out =rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)
return self.to_out(out)
イメージは\((QK^T)V\)を\(Q(K^TV)\)という形にして、先に\(K^TV\)を計算することで\(O(n^2)\)にならないようにしています(\(dim\times dim\)になります)。
Group Normalization
Group Normalizationは2018年に以下の論文で提案されたバッチ正規化(Batch Normalization)の改良版です。
以下の論文の図の一番右側がGroup Normalizationです。
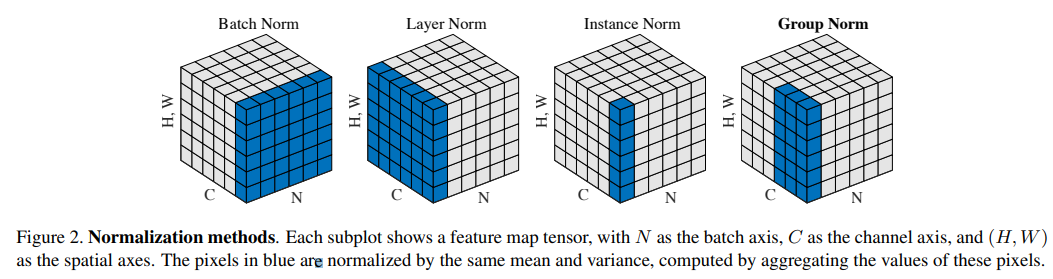
バッチ正規化(Batch Normalization)では、各チャネルごとにバッチ×縦・横の平均・標準偏差で正規化していましたが、Group Normalizationでは1つのバッチだけを使い、チャネル、縦、横の平均・標準偏差で正規化します。
ただし、全チャネルを使うのではなく、チャネルのグループを決め、そのグループで計算します。
詳しくはこちらの記事をご参照ください。
では、ある処理\(f(x)\)の前にGroup Normalizationを行うPreNormクラスを作成しておきます。
PreNormはattentionの前にGroup Normalizationを適用する形で使用します。
Group Normalizationはtorch.nn.GroupNorm()関数を使います。
nn.GroupNormの引数には、グループの数を表すnum_groups、チャネル数を表すnum_channelsを指定します。
num_channelsはnum_groupsで割り切れないといけませんのでご注意ください。
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.fn = fn
self.norm = nn.GroupNorm(num_groups=1, num_channels=dim)
def forward(self, x):
x = self.norm(x)
return self.fn(x)
U-Netの作成
非常に長くなりましたが、以上で、U-Netで必要なパーツはすべて作成しました。
では、これらのパーツを使って、U-Netを構築してみましょう。
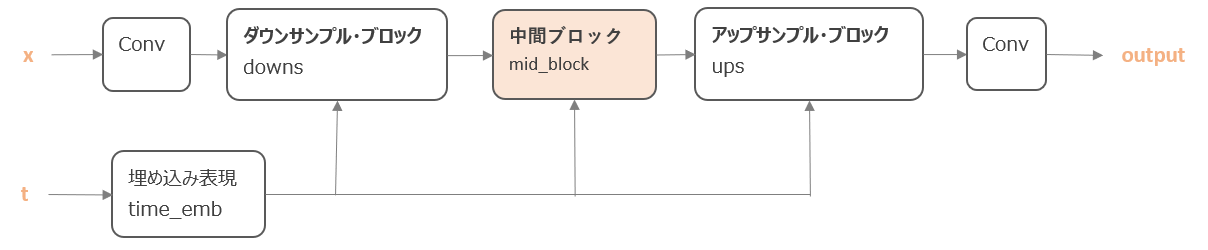
全体像は以下のように、畳み込み → ダウンサンプル → 中間ブロック → アップサンプル → 畳み込み、という順で処理をしていきます。
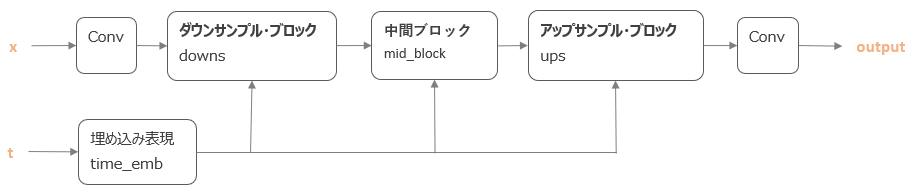
また、ダウンサンプル、中間、アップサンプル時には、時点を表す情報の埋め込み表現もインプットとして利用します。
class Unet(nn.Module):
def __init__(
self,
dim,
init_dim=None,
out_dim=None,
dim_mults=(1, 2, 4, 8),
channels=3,
with_time_emb=True,
resnet_block_groups=8,
):
super().__init__()
self.channels = channels
init_dim = default(init_dim, dim // 3 * 2)
self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3)
dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:])) # (input_dim, output_dim)というタプルのリストを作成する
resnet_block = partial(ResnetBlock, groups=resnet_block_groups)
# time embeddings
if with_time_emb:
time_dim = dim
# time_mlp: pos emb -> Linear -> GELU -> Linear
self.time_mlp = nn.Sequential(
SinusoidalPositionEmbeddings(dim),
nn.Linear(dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
else:
time_dim = None
self.time_mlp = None
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out) # blockを処理する回数
# ダウンサンプル
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(
nn.ModuleList(
[
resnet_block(dim_in, dim_out, time_emb_dim=time_dim),
resnet_block(dim_out, dim_out, time_emb_dim=time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
DownsampleConv(dim_out) if not is_last else nn.Identity(),
]
)
)
# 中間ブロック
mid_dim = dims[-1]
self.mid_block1 = resnet_block(mid_dim, mid_dim, time_emb_dim=time_dim)
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = resnet_block(mid_dim, mid_dim, time_emb_dim=time_dim)
# アップサンプル
for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):
is_last = ind >= (num_resolutions - 1)
self.ups.append(
nn.ModuleList(
[
resnet_block(dim_out * 2, dim_in, time_emb_dim=time_dim),
resnet_block(dim_in, dim_in, time_emb_dim=time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
UpsampleConv(dim_in) if not is_last else nn.Identity(),
]
)
)
out_dim = default(out_dim, channels)
self.final_conv = nn.Sequential(
resnet_block(dim, dim),
nn.Conv2d(dim, out_dim, 1)
)
def forward(self, x, time):
x = self.init_conv(x)
t = self.time_mlp(time) if exists(self.time_mlp) else None
h = []
# ダウンサンプル
for block1, block2, attn, downsample in self.downs:
x = block1(x, t)
x = block2(x, t)
x = attn(x)
h.append(x)
x = downsample(x)
# 中間
x = self.mid_block1(x, t)
x = self.mid_attn(x)
x = self.mid_block2(x, t)
# アップサンプル
for block1, block2, attn, upsample in self.ups:
x = torch.cat((x, h.pop()), dim=1) # downsampleで計算したhをくっつける
x = block1(x, t)
x = block2(x, t)
x = attn(x)
x = upsample(x)
return self.final_conv(x)
ちょっと長いですのでブロックの中身を見ていきましょう。
時点情報の埋め込み表現を計算
まずは以下のオレンジ色の部分の時点情報の埋め込み表現を計算する部分です。
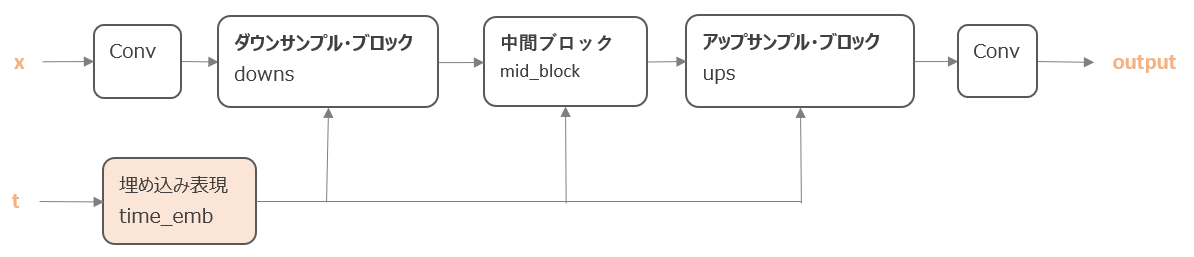
こちらは、まず、作成したSinusoidalPositionEmbeddingsクラスにより、sin・cos関数を使って時点情報の埋め込み表現を作成します。
それを「全結合 → 活性化関数 → 全結合」により最終的に付加する値を計算します。
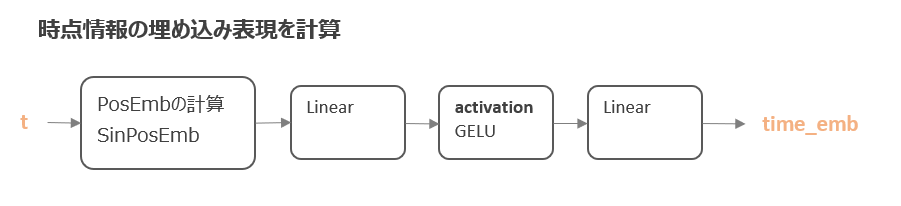
コードでは以下が対応します。
23行目から、nn.Sequentialで一連の処理を作成しています。
# time embeddings
if with_time_emb:
time_dim = dim
# time_mlp: pos emb -> Linear -> GELU -> Linear
self.time_mlp = nn.Sequential(
SinusoidalPositionEmbeddings(dim),
nn.Linear(dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
else:
time_dim = None
self.time_mlp = None
forwardメソッドの対応する箇所は85行目です。
t = self.time_mlp(time) if exists(self.time_mlp) else None
ダウンサンプル・ブロック
続いて、ダウンサンプル・ブロックです。
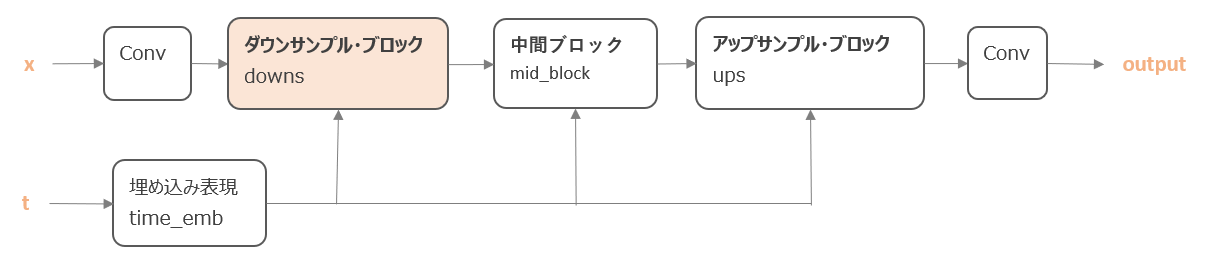
ダウンサンプル・ブロックは以下のように、「残差結合ブロック → 残差結合ブロック → Attention → 畳み込み処理」という順番になっています。
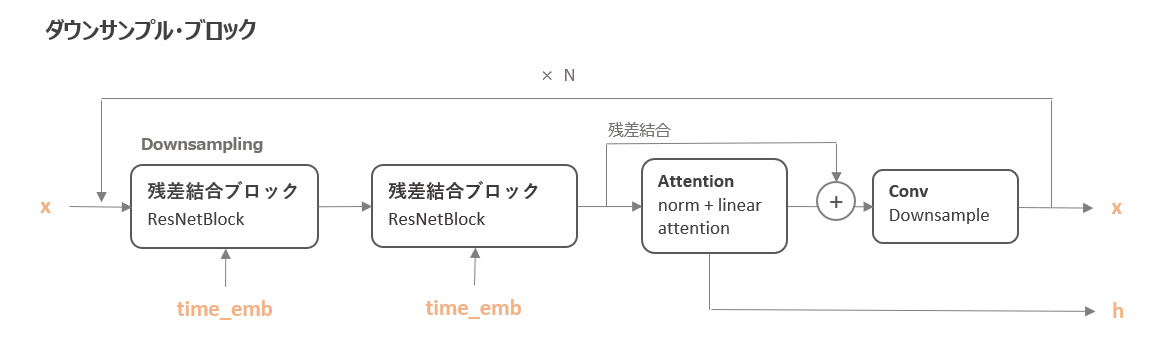
xともう一つ出力しているhは、アップサンプル時に利用するものです。
コードは以下の抜粋部分が対応します。
「残差結合ブロック → 残差結合ブロック → Attention → 畳み込み処理」というブロックを変数in_outの回数(num_resolutions)だけループして作成しています。
in_outは(input_dim, output_dim)の組合せのリストです。
# ダウンサンプル
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(
nn.ModuleList(
[
resnet_block(dim_in, dim_out, time_emb_dim=time_dim),
resnet_block(dim_out, dim_out, time_emb_dim=time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
DownsampleConv(dim_out) if not is_last else nn.Identity(),
]
)
)
最後は一番最後の処理は畳み込みではなくnn.Identity()となっています。
forwardメソッドの中身では以下が対応します。
# ダウンサンプル for block1, block2, attn, downsample in self.downs: x = block1(x, t) x = block2(x, t) x = attn(x) h.append(x) x = downsample(x)
中間ブロック
次に、中間ブロックです。
中間ブロックは、「残差結合ブロック → attention → 残差結合ブロック」という順番で処理をします。
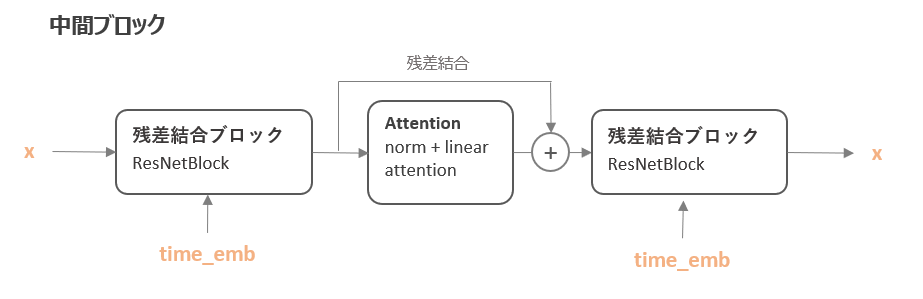
コードでは以下のブロックが対応します。
# 中間ブロック mid_dim = dims[-1] self.mid_block1 = resnet_block(mid_dim, mid_dim, time_emb_dim=time_dim) self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim))) self.mid_block2 = resnet_block(mid_dim, mid_dim, time_emb_dim=time_dim)
Attentionの処理の前にPreNormクラスでGroupNormalizationを使い、さらにResidualにより残差結合を行っています。
forwardメソッドでは以下が対応します。
# 中間 x = self.mid_block1(x, t) x = self.mid_attn(x) x = self.mid_block2(x, t)
アップサンプル・ブロック
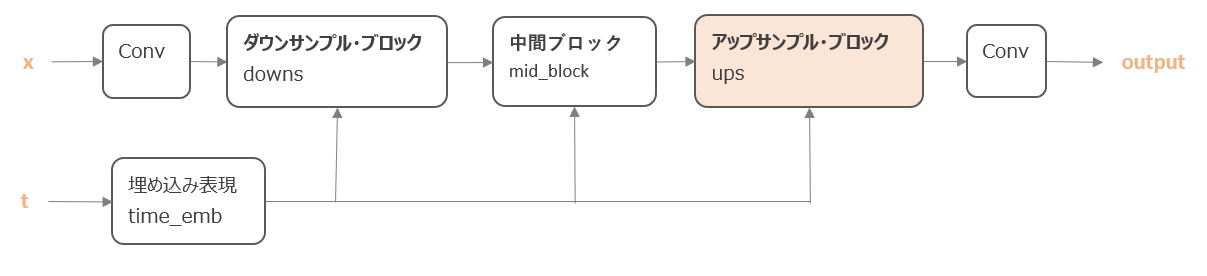
アップサンプルもダウンサンプルとほぼ同じで、「残差結合ブロック → 残差結合ブロック → Attention → 畳み込み処理」という順で処理をします。
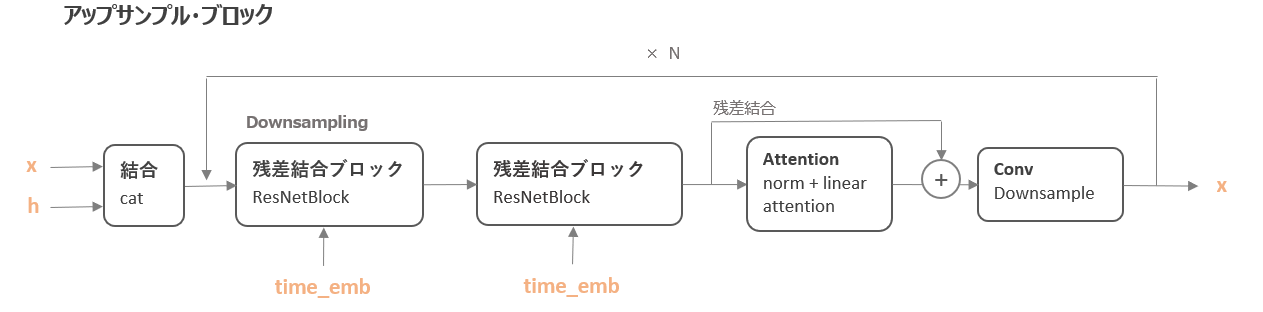
コードでは以下が対応します。
# アップサンプル
for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):
is_last = ind >= (num_resolutions - 1)
self.ups.append(
nn.ModuleList(
[
resnet_block(dim_out * 2, dim_in, time_emb_dim=time_dim),
resnet_block(dim_in, dim_in, time_emb_dim=time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
UpsampleConv(dim_in) if not is_last else nn.Identity(),
]
)
)
forwardメソッドでは以下が対応します。
# アップサンプル for block1, block2, attn, upsample in self.ups: x = torch.cat((x, h.pop()), dim=1) # downsampleで計算したhをくっつける x = block1(x, t) x = block2(x, t) x = attn(x) x = upsample(x)
長い道のりでしたが以上でU-Netが完成しました!
動作確認
では、ちゃんと動くかここで確認しておきましょう。
まずは、パラメータを設定します。
image_size = 128 channels = 3 batch_size = 8 timesteps = 200
そして、U-Netのモデルをインスタンス化します。
model = Unet(
dim=image_size,
dim_mults=(1, 2, 4, 8),
channels=channels,
with_time_emb=True,
resnet_block_groups=2,
)
投入する画像データと時点\(t\)の情報を作成します。
data = torch.randn((batch_size, channels, image_size, image_size)) t = torch.randint(0, timesteps, (batch_size,)).long()
では、モデルで処理してみましょう。
output = model(data, t) output.size()
これでエラーにならずに8×3×128×128の配列が返って来ればいったんは大丈夫です!
まとめ
今回は、Diffusionモデルで使われているニューラルネットワークであるU-Netを実装しました。
これでDiffusionモデルを学習するパーツはそろいましたので、次回は実際に学習するためのコードを実装していきたいと思います。
では!!



