さて、今回はOpenAIから提案された、attentionを効率化することで長い系列を取り扱うことを可能にしたSparse Transformerの論文について解説したいと思います。
この仕組みはGPT-3やDALL-Eなどでも使われている技術です。
ほかにもLongformerなど、Sparse Transformerを発展させたモデルもありますので、そちらもご参照いただければと思います。
もとの論文はこちらです。
『Generative Modeling with Sparse Transformer』
Transformerと言えば自然言語処理分野で主流となっているモデルですが、このSparse Transformerでは文章だけでなく、画像や音楽の生成にも応用しています。
以下は、Sparse Transformerによって生成された画像です。(おじさんが気になってしょうがないですが…)
音楽は“https://openai.com/blog/sparse-transformer”から聞くことができます。

よくわからない画像もありますが、各画像において最初から最後まで内容が一貫していることはわかります。
つまり、長距離の依存関係をきちんと捉えているというです。
これが近くの依存関係しか捉えていないと、画像の初めと最後の方で全く関係のない画像になってしまいます。
これでだいぶわかってきたかもしれませんが、Sparse Transformerは、Transformerでは扱えないような長い系列を処理するためのモデルです。
Transformerをよく知らないという方は、まずTransformerを押さえた方が良いと思いますので、以下の記事をご参照ください。
では、論文に沿って詳細を見ていきましょう。
目次
Sparse Transformerとは
Self-attentionを使ったTransformerは非常に汎用性の高い極めて優れたアーキテクチャです。
ただ、Transformerにも欠点はあり、それは長い系列を扱うことが難しいということです。
Dot-Product Attentionの\(QK^T\)のところでattentionを向ける場所を\(n\times n\)で表現するため(\(n\)はインプット系列の長さ)、メモリの使用量がインプット系列の長さの二乗に比例し、系列が長くなるほど処理の負荷が高くなります。
以下は、各データの種類ごとのattentionで使うメモリ量です。

1024単語のテキスト情報で1GBです。
それなりに長い情報を扱おうとすると1024単語以上になることはよくあります。
画像になると解像度が32×32で9.6GB、64×64で154GB、音楽あと24,000サンプルで590GBととてもGPUで処理できる量ではありません。
そこで、使うメモリ量を減らすためSparse Transformerではattentionの向け方を工夫します。
従来のTransformerのattentionでは、自分自身とそれより前の部分にすべてにattentionを向けますので、それが\(O(n^2)\)のメモリ使用量になっていました。
これを、自分より前の単語すべてではなく、自分より前の単語の一部分に限定することにより、\(O(n\sqrt{n})\)のメモリ使用量にします。
つまり、attentionを向ける先をsparse(疎)にするということです。
では、どのようにsparseにするか、など詳細を見ていきましょう。
Sparse TransformerのAttention
どこにattentionを向けるべきか
Sparse Transformerではattentionを向ける先を限定すると言いましたが、どこに限定すれば良いかを見ていきましょう。
以下の図はTransfomerの各レイヤーにおいて、attentionが向いている先を表しています。
黒い部分がマスクなので、黒い部分の直前のピクセルまで画像が生成されているということです。
そして、光っているところが大きくattentionを向けている先です。

例えば、左上のaの図は下位のレイヤーですが、生成されているピクセルの直前が光っているので、そこにattentionが向いていることがわかります。
つまり下位レイヤーは、自分自身の直前の情報に注意を向けており、局所的な情報を見ていると言えます。
右上の図bは19番目、20番目のレイヤーですが、左の4つは行方向(横方向)にattentionが向いており、右の4つは列方向(縦方向)にattentionが向いていることがわかります。
cでは画像によって違ってきており、画像全体に散らばってattentionが向いています。
dは64-128番目のレイヤーで、かなりまばらになってきています(いまいちどこにattentionが向いているのかわかりませんが)。
Sparse Transformerでは、これらの特徴を捉えたattentionを検討します。
Sparse Transformerのattention
以上の考察より、効率的なattentionの向け先を考えます。
Sparse Transformerでは以下の図の(b)、(c)のattentionを使います。
上は6×6の画像の場合の例で、下の図はattentionマトリックスです。
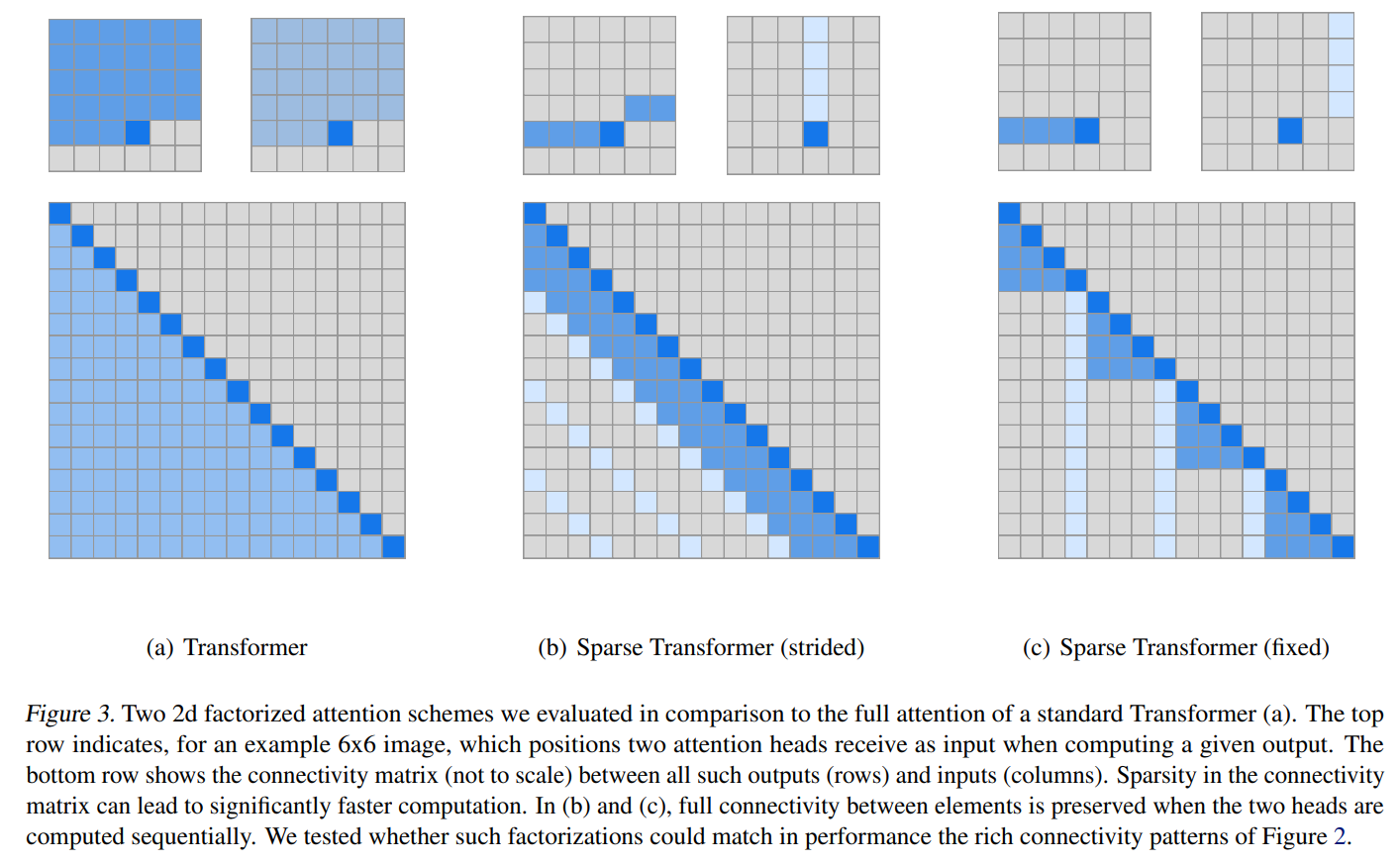
では、順番に見ていきましょう。
通常のattention(Full attention)
一番左の(a)は通常のTransformerです。

上の図を見てもわかる通り、自分より前の位置すべてにattentionを向けています。
下段の図のattentionマトリックスで言うと、自分より左、つまり自分より前の位置すべてにattentionを向けています。
Strided attention
(b)はSparse Transformerで提案されているattentionで、“strided attention”と呼ばれるものです。

2つのヘッドに分けて、1つ目がヘッドが濃い青のattention、2つ目のヘッドが薄い青のattentionです。
まず、下の図から見ていくと、濃い青の方は、自分より前の位置すべてにattentionを向けるのではなく、直前の3つの位置だけにattentionを受けています。
このように、自分の位置から直前のいくつ、という形でattentionを向けます。
そして、薄い青の方は、3つおきにattentionを向けています。
これを画像で表すと、上段の図になります。
薄い青は縦にattentionを向けていることがわかります。
前の画像で見たattentionのパターンですね。
このようなattentionは、画像や音楽など周期的な傾向のあるデータに関して有効と考えられます。
Fixed attention
(c)は、Sparse Transformerで提案されているもう一つのattentionパターンである、”fixed attention”です。
(b)のstride attentionが相対的だったのに対し、(c)ではそれに絶対的な位置の要素も付け加えます。
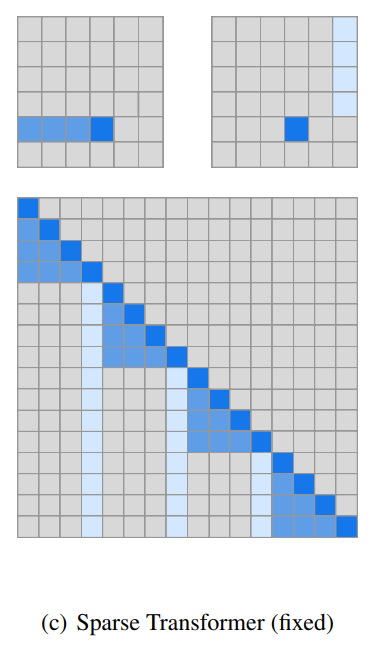
濃い青は、自分より前のいくつかですが、いくつと固定はされていません。
上段の画像の例では、自分より左側にattentionを向けていることがわかります。
薄い青は一定の位置において縦のラインすべてにattentionを向けています。
上の図で見ると、特定縦の列にattentionが向いています。
このように特定の位置のインプットにattentionを向けます。
これは、後で詳しく見ていきますが、このfixed attentionパターンは文章などのテキスト情報に有効という結果が出ています。
数式による定式化
以上で感覚的にどういったattentionがあるのかわかったと思います。
これをもう少し厳密に数式で表現しましょう。
まず、\(X\)をインプットとします。
そして、\(S=\{S_1, \cdots, S_n\}\)、\(S_i\)を\(i\)番目のインプットがattentionを向ける先のインデックスを表すものとします。
例えば、10番目のインプットが1, 4, 7番目のインプットにattentionを向ける場合、\(S_{10}=\{1, 4, 7\}\)です。
そして、attentionは、
$$\begin{align}
\text{Attend}(X, S)=\left(a({\bf{x}}_i, S_i)\right)_{i\in\{1,\cdots,n\}}
\end{align}$$
と表します。
\(i\)番目のインプット\(x_i\)の値とattentionを向ける先\(S_i\)を使って計算します。
そして、Dot-Product attentionです。
\({\bf{x}}_i\)の向けるattentionは以下で表されます。
$$\begin{align}
a({\bf{x}}_i, S_i)=\text{softmax}\left( \frac{(W_q{\bf{x}}_i)K_{S_i}^T}{\sqrt{d}} \right)V_{S_i}
\end{align}$$
queryは\(W_q{\bf{x}}_i\)なので特に変わりはありません(Transformerの論文でいう\(Q\)です)。
ポイントは、keyとvalueがそれぞれ\(K_{S_i}\)と\(V_{S_i}\)になっている箇所です。
すべてにattentionを向けるのではなく、\(S_i\)だけにattentionを向けますので、
$$\begin{align}
K_{S_i}&=\left( W_k{\bf{x}}_j\right)_{j\in S_i}, \\
V_{S_i}&=\left( W_v{\bf{x}}_j\right)_{j\in S_i}
\end{align}$$
というように表します。
\({\bf{x}}_j\)の\(j\)は\(S_i\)に含まれているものだけですので、そこだけを計算することになります。
これで、\(K\)のサイズが小さくなり、メモリ使用量を減らすことが可能になります。
特にattentionを向ける先の数を\(\sqrt{n}\)に近い値にすることで、メモリの使用量が\(O(n^2)\)から\(O(n\sqrt{n})\)にすることが可能です。
Transformerのattention
通常のTransformerの場合は、\(S_i=\{j:j\le i\}\)となります。
自分自身とそれより前すべてにattentionを向けるということになります。
繰り返しになりますが、Sparse Transformerでは、この\(S_i\)の要素を減らすことを考えます。
とくに、\(S_i\)の要素をインプットの長さ\(n\)に対して\(\sqrt{n}\)になるように選ぶことで、メモリ使用量を\(O(n\sqrt{n})\)とします。
では、先ほど図で見た2つのattentionパターンについて、定式化していきます。
Strided Attention
(b)のパターンです。
attentionを2つのヘッドに分けます。
これは、上図で見た濃い青色と薄い青色のattentionに対応します。
1つ目のヘッドのattentionは、直前の\(l\)個のインプットにattentionを向けます。
つまり、
$$A_i^{(1)}=\{t, t+1, \cdots, i\}, \hspace{10pt} t=\max(0, i-l)$$
とします。
\(i\)番目から、\(i-l\)番目までにattentionを向けるということですね。
そして、2つ目のヘッドのattentionを、
$$A_i^{(2)}=\{j:(i-j)\mod l=0\}$$
とします。
\(i\)が自分自身の位置になので、差が\(l\)の倍数となるような\(j\)ということで、“自分自身から\(l\)個ずつ離れた場所すべて”になります。
薄い水色部分ですね。
Fixed Attention
次に(c)のパターンのFixed attentionパターンです。
1つ目のヘッドを
$$A_i^{(1)}=\{j:(\lfloor j/l \rfloor =\lfloor i/l \rfloor \}$$
とします。\(\lfloor \cdot \rfloor\)はフロア関数を表します。
わかりづらいですが、\(l\)は間隔(stride)で、自分自身の位置\(i\)をそれで割って商が同じになるということなので、ようは“自分自身とそれより前の割り切れる位置までの間すべて”ということになります。
そして、2つ目のヘッドは、
$$A_i^{(2)}=\{j: j \mod l \in\{t,t+1, \cdots, l\}, \hspace{15pt} t=l-c\}$$
とします。
\(c\)はハイパーパラメータです。
こちらはさらにややこしいのですが、\(l=128\)、\(c=8\)とすると、\(t=120\)となります。
ですので、128で割ったときのあまりが120, 121, ..., 128なので、128より大きい位置のインプットはすべて120, 121, ..., 128番目にattentionを向けます。
本論文では\(c\in\{8, 16, 32\}\)、\(l=\{128,256\}\)とします。
\(c\)を増やせば増やすほど、attentionを向ける先が多くなり、計算量が増加します。
Sparse Transformer全体
それでは、sparse attentionについて理解できたところで、Sparse Transformer全体について説明します。
まず、最終的なattention層のアウトプットは、
$$\text{attention}(X)=W_p\cdot\text{attend}(X,S)$$
とします。
\(\text{attend}(X,S)\)で、どこにどれだけattentionを向けるかというのを計算し、それに重み行列を掛けています。
上述の複数のヘッドによってattentionの仕方が違うsparse attentionの仕組みを取り込んでいきます。
これには複数の方法があります。
一つは、各レイヤーによって\(A^{(1)}\)を使うか\(A^{(2)}\)を使うかを変える方法です。
\(p\)個のヘッドを考える場合は以下のように表されます。
$$\text{attention}=W_p\cdot\text{attend}(X,A^{(r \mod p)})$$
\(p=2\)であれば、\(A^{(1)}\)と\(A^{(1)}\)を交互に使います。
もう一つの方法は、2つのattentionを混ぜてしまう方法です。
$$\text{attention}=W_p\cdot\text{attend}(X,\cup_{m=1}^p A^{(m)})$$
3つ目の方法は、TransformerのMulti-head attentionのようにヘッドごとに分けて、結果を連結させる方法です。
$$\text{attention}=W_p\left(text{attend}(X,A)^{(i)}\right)_{i\in\{1,\cdots,n_h\}}$$
全体の構成
少しだけTransformerとは変更されています。
左がSparse Transformer、右がTransformerのデコーダのTransformerブロックだけを抜き出したものです。
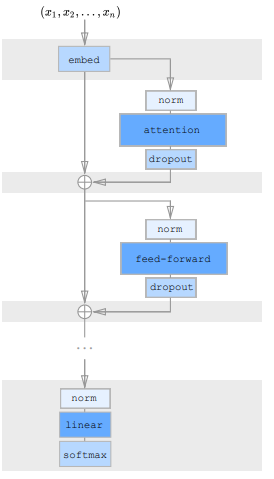
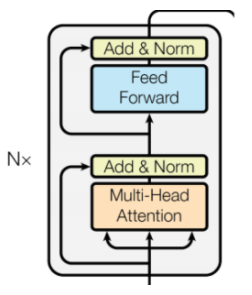
向きが逆でわかりにくいかもしれませんが、Normalization層がattention層やfeed forward層の後に来ていましたが、Sparse Transformerでは前に来ています。
では、順番に見ていきましょう。
まず、インプットの埋め込み表現を求めます。
$$H_0=\text{embed}(X,W_i)$$
そして、\(k\)番目のレイヤーでは、その前のレイヤーのアウトプットとresblockのアウトプットについて残差結合を行います。
$$H_k=H_{k-1}+\text{resblock}(H_{k-1})$$
ここでresblockは以下のように\(a(H)\)と\(b(H)\)の和で表されます。
$$\begin{align}
\text{resblock}(H)&=a(H)+b(H)
\end{align}$$
\(a(H)\)は以下の部分で、attention層の部分です。
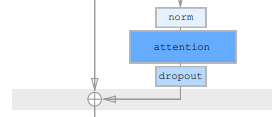
$$\begin{align}
a(H)&=\text{dropout}(\text{attention}(\text{norm}(H)))\\
\end{align}$$
と表されます。
そして、\(b(H)\)は以下のFeed Forward層の部分です。
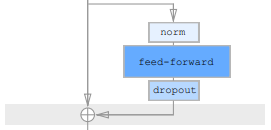
$$\begin{align}
b(H)&=\text{dropout}(\text{FeedForward}(\text{norm}(H+a(H))))\\
\end{align}$$
と表されます。
それらを残差結合して次の(Sparse)Transformerブロックに渡します。
これを\(N\)回繰り返します。
最後は、それを正規化して、softmax層を通します。
$$y=\text{softmax}(\text{norm}(H_N)W_{out})$$
なお、Feed Forward層の活性化関数はBERTやGPTなどで使われているGELUを使います。
色々な種類のデータに対応する
Transformerでは、位置情報をpositinal encoding(positional embedding)として付加していました。
Sparse Transformerでも同様に位置情報を考慮したインプットの埋め込み表現\(\text{embed}(X, W_e)\)を計算しますが、以下のようにすることでデータの構造やattentionパターンに関する情報も付加します。
$$\text{embed}(X,W_e)=\left({\bf{x}_i}W_e+\sum^{n_{emb}}_{j=1}{\bf{o}}_i^{(j)}W_j\right)_{{\bf{x}}_i\in X}$$
ここで、画像の場合、\(n_{emb}=d_{data}\)(\(d_{data}\)はインプットの次元=3)、テキスト・音声の場合は\(n_{emb}=d_{attn}\)(Sparse Transformerのattentionの次元=2)とします。
また、\({\bf{o}}_i^{(j)}\)は\(i\)番目のインプットの\(j\)番目の次元であるということを表すone-hotベクトルです。
その他のテクニック
他にも“Gradient checkpoints”という手法でメモリ使用量を減らしたり、効率的にSparse Attentionを計算したりしていますので、ご興味のある方は論文をご参照ください。
『Training Deep Nets with Sublinear Memory Cost』
Gradient checkpointsは、バックプロパゲーションの際に、メモリの利用を効率化することで、レイヤー数を増やしてもメモリの使用量が大きく増えないようになります。
それにより、レイヤー数を大幅に増やすことができるというものです。
実験結果
では、Sparse Transformerの実験結果を見ていきましょう。
ここでは、画像データセットであるCIFAR-10、ImageNet 64×64と、自然言語処理用データセットEnwiki8、クラシック音楽のデータセットを使って学習します。
各データセットの結果は以下のようになっています。
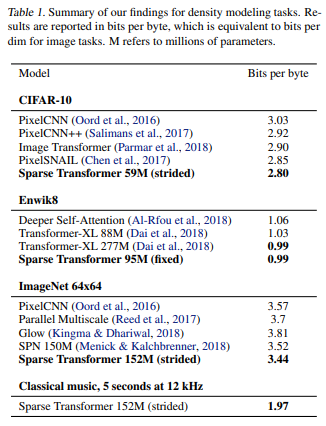
では、個別に見ていきましょう。
CIFAR-10
CIFAR-10は解像度が32×32なので、インプットは32×32×3の3072個の系列になります。
そして、48000サンプルを学習データに2000サンプルをテストデータにしています。
2.80 bits per byteと当時のSoTAを更新しています(上表Table 1)。
bits per byteはbits per dimensionと同じで、1ピクセル単位当たりの負の対数尤度みたいなものです。
ですので、小さい方が精度が良いということになります。
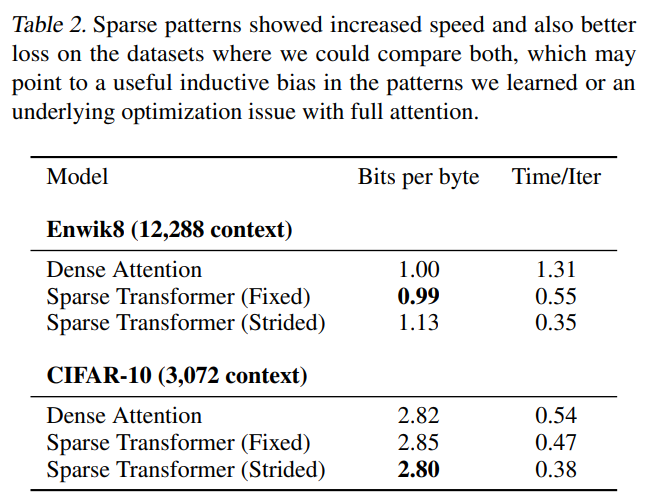
また、attentionの違いによっても精度を見ています。
下段のCIFAR-10だとStrided attentionを使うのが精度が高く、Fixed attentionでは精度が悪化しています。
Enwik8
では、長いテキスト情報を使った精度を見ていきましょう。
EnglishWikipediaのインプットは12,288個と非常に長い文章になっています。
Transformer-XLと同程度の0.99bits per byteとなっています(Table 1)。
Transformer-XLの方は277Mパラメータなのに対して、Sparse Transformerはその約3分の1の95Mパラメータで達成しています(Transformerも長文に対応したTransformerですが、attentionはほぼfull attentionになっています)。
また、attentionの種類による比較では、Fixed attentionが良く、Strided attentionでは精度がかなり悪化しています。
計算時間も通常のattentionよりもかなり短くなっています。
ImageNet 64x64
ImageNet 64x64では、32×32よりも長い系列を取り扱う必要があります。
Strided attentionで3.44 bits per byteと、こちらも非常に良い結果になっています。
また、以下はImageNet 64x64で学習し、画像の一部を与えるというようなことはせず、そのまま生成した画像です。
よくわからない画像もありますが、基本的には初めから最後まで一貫した画像になっていると思います。

Classical Music from Raw Audio
こちらは聴いていただいた方が早いので、ご興味のある方はこちらのOpenAIのブログから聴いてみてください。
5秒ごとに違うサンプルです。
(過去のモデルだとどんな感じかわからないので、いまいちすごいのかどうかわかりません…)
まとめ
今回はOpenAIによるattentionを効率化することにより、長い系列を処理することができるSparse Transformerを見てきました。
これに続いて、LongformerなどSparse Transformerをさらに改良したようなモデルが出てきていますので、そちらもご覧いただければと思います。
では、また!

