前回の記事ではGANの評価指標としてよく用いられているInception Scoreについて解説しました。
今回はもう一つの代表的な評価指標であるFrechet Inception Distance(FID)について解説したいと思います。
Inception Scoreは人間の感覚に比較的合っている指標とされているものの、本物の画像と比較をしていないという欠点がありました。
そこで、FIDでは本物の画像の情報も精度評価に使おうというものです。
FIDはInception Scoreと同様にInception-v3モデルを使って、本物と生成された画像それぞれの埋め込み表現を計算し、それらの平均と共分散を比較し、その距離が近い、つまり値が小さいほど良いスコアということになります。
では見ていきましょう。
論文はこちらになります。
『GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium』
Frechet Inception Distanceとは
Frechet Inception Distanceを計算する際は、現実の画像の埋め込み表現の分布と生成された画像の埋め込み表現の分布がそれぞれ多変量正規分布に従うと考えます。
(FIDでは計算に平均・分散を使うからというだけなので、あまり深く考えなくても大丈夫です)
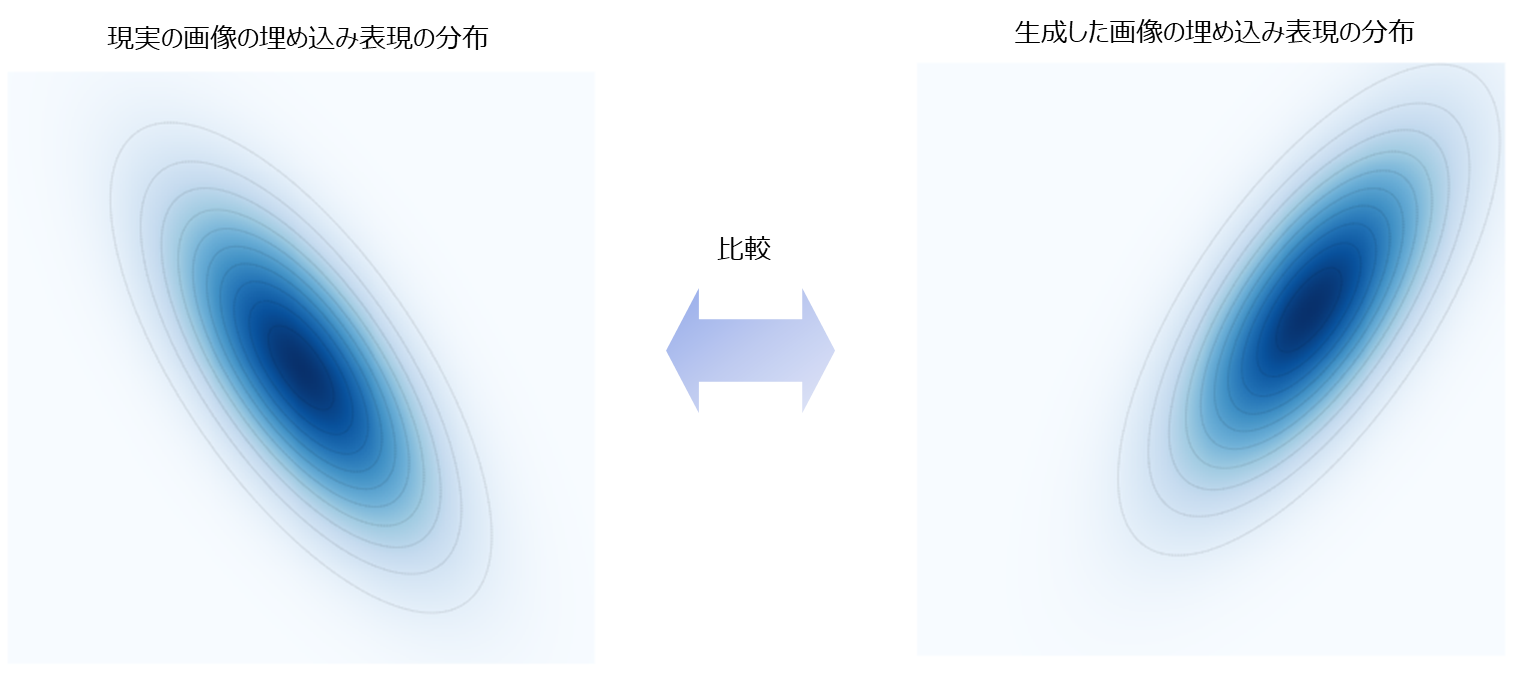
そして、現実の画像の平均・分散と生成された画像の平均・分散を比較することによって、生成された画像がどれだけ現実の画像に近いかを評価します。
ただし、生成された画像の各ピクセルの平均・分散を使うと位置がずれているだけで全然違う画像という評価になってしまうので、FIDでは各画像から埋め込み表現を計算し、その平均・分散を比較します。
埋め込み表現を求めるために利用するモデルは、Inception Scoreと同様にInception-v3モデルを使います。
まず、Inception-v3の最後のPoolingレイヤーのアウトプットをその画像の埋め込み表現と、大量の画像に対して埋め込み表現を求めます。
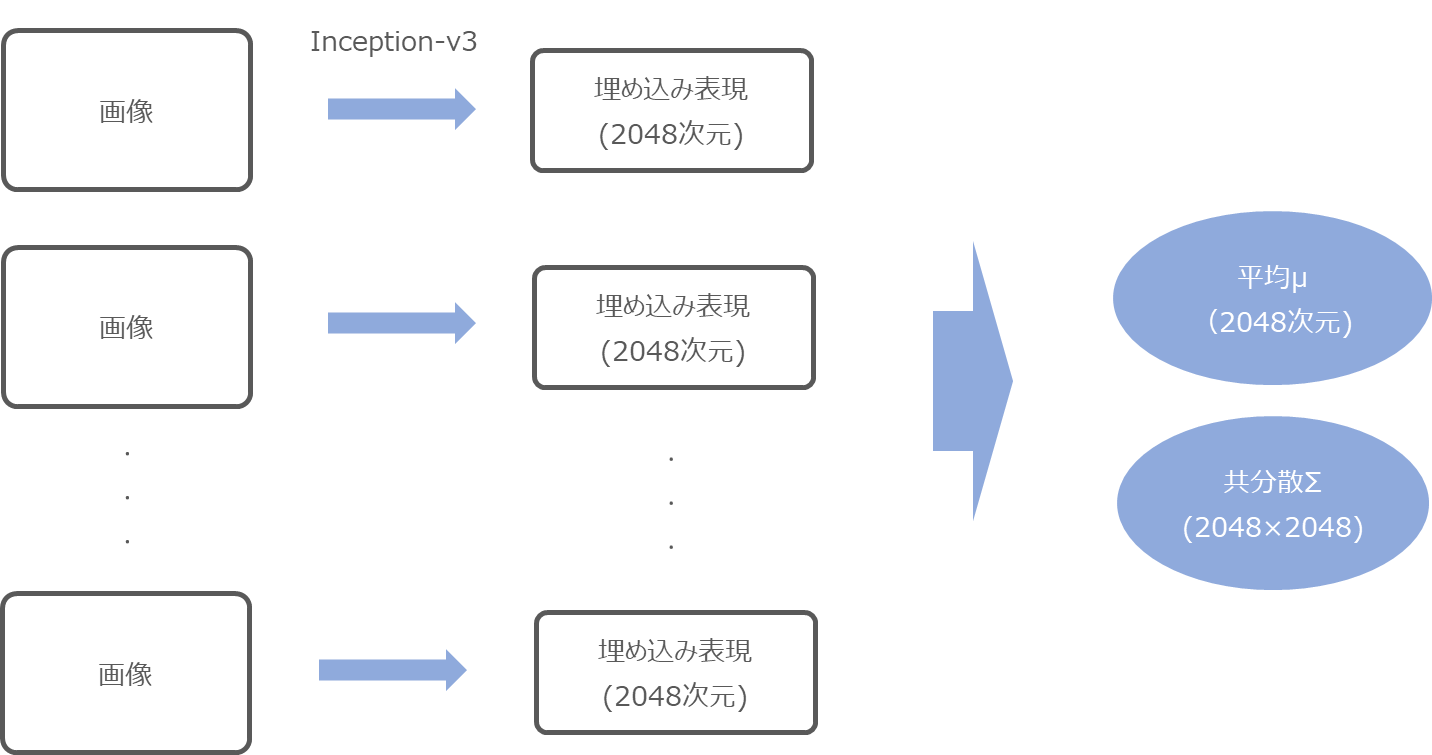
これを本物の画像と生成された画像それぞれにについて行います。
そして、本物の画像と生成された画像それぞれについて、埋め込み表現の平均・共分散を求めます。
これらの平均(\(\mu_X\), \(\mu_Y\))・共分散(\(\Sigma_X\), \(\Sigma_Y\))について、以下のような距離で計測します。
$$\begin{align}
\text{FID}=\|\mu_X-\mu_Y\|^2 +\text{Tr}\left(\Sigma_X+\Sigma_Y-2\sqrt{\Sigma_X\Sigma_Y}\right)
\end{align}$$
\(\text{Tr}\)はトレース(対角線上の要素の合計)を意味しています。
この距離がFIDになります。
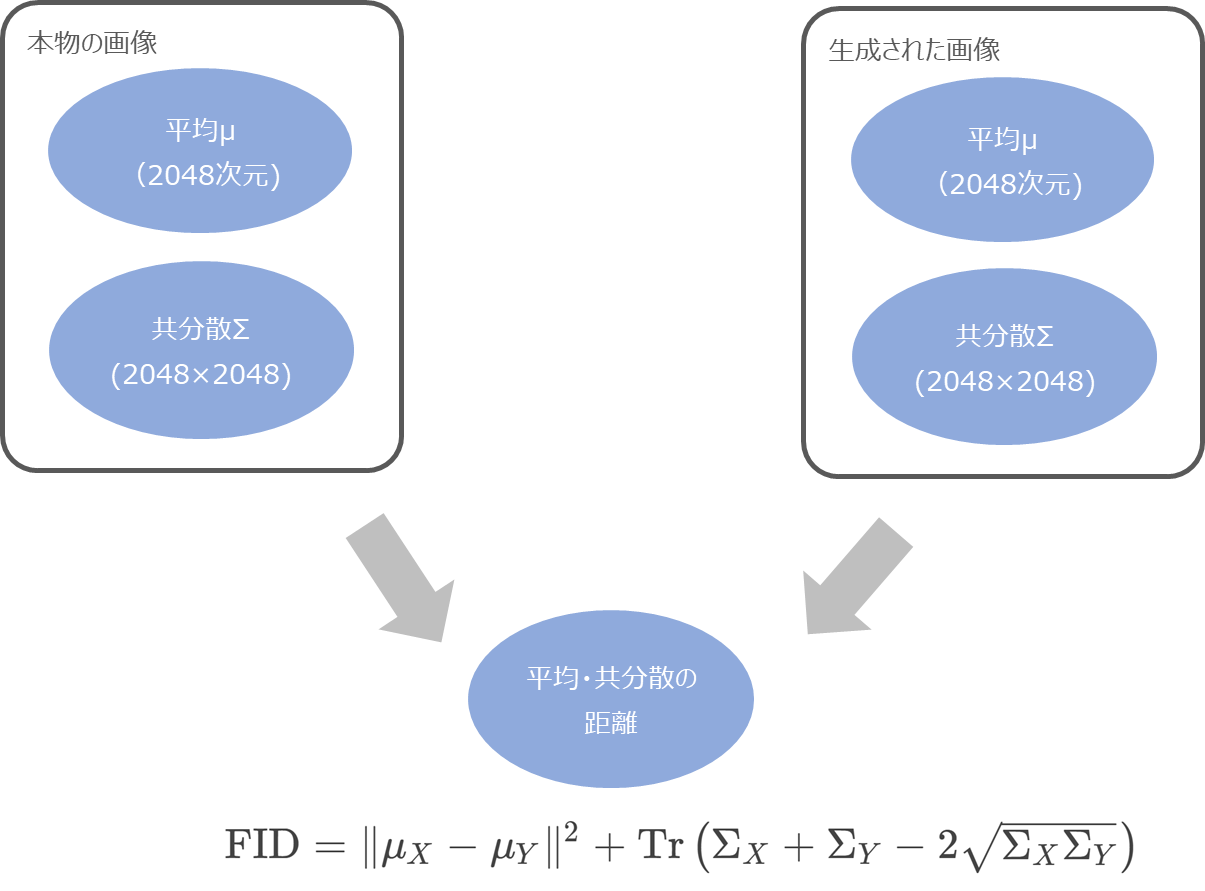
ここからわかるように、FIDは小さければ小さいほど良いと考えられる指標です。
実装イメージ
今回はGANを実装するわけではないので、GANのモデルはgeneratorとして既にあるものとして、FIDを計算する過程のみを説明していきます。
実際に計算したい人はこちらのTensorflowの公式実装もしくはPyTorchの実装をお使いください。
流れとしては、まず、学習済みInception-v3をロードします。
GANのgeneratorで画像を生成し、実際の画像と生成された画像を299x299のサイズにリサイズします。
次に、ロードした学習済みInception-v3モデルを使って生成された画像の埋め込み表現を計算します。
# 埋め込み表現を求める real_embeddings = model.predict(real_images) fake_embeddings = model.predict(fake_images)
そして、FIDは以下の式で表されるので平均・共分散と行列の平方根を計算します。(行列の平方根は複素行列になる場合があるので、実数部分だけを使っています)
$$\begin{align}
\text{FID}=\|\mu_X-\mu_Y\|^2 +\text{Tr}\left(\Sigma_X+\Sigma_Y-2\sqrt{\Sigma_X\Sigma_Y}\right)
\end{align}$$
# 平均・分散・行列の平方根を計算する from scipy.linalg import sqrtm real_mu = real_embeddings.mean(axis=0) real_sigma = cov(real_embeddings, rowvar=False) fake_mu = fake_emeddings.mean(axis=0) fake_sigma = cov(fake_embeddings, rowvar=False) covmean = sqrtm(real_sigma.dot(fake_sigma)).real
あとは、上記の式に従って計算するだけです。
# FIDを計算する fid = numpy.sum((real_mu - fake_mu)**2.0) + trace(real_sigma + fake_sigma - 2.0 * covmean)
計算は以上です。
欠点
FIDも欠点はあり、例えば以下のようなものが挙げられます。
学習済みモデルを利用する
Inception Networkという学習済みモデルで埋め込み表現を評価していました。
このInception NetworkはImageNetで学習しているのですが、もちろんすべての画像に対応しておらず、もしアニメの画像などを評価したい場合、Inception Networkで計算された埋め込み表現は良い埋め込み表現になっていないと考えられます。
平均と分散のみを利用している
平均と分散しか使っていないので、それ以外の情報はすべて捨てていることになります。
分布が全く違っても、同じような平均と分散を取るということはあり得るので、その平均・分散だけを見てモデルの良し悪しを判断すると間違った結果になる可能性があります。
たくさんのサンプル数が必要
平均・分散を計算するのでサンプル数が多く必要になってきます。
少ないサンプルで平均・分散を比較しても、外れた画像の存在により、正しい結果にならない可能性があります。
だいたい1万サンプル以上が推奨されています。
計算が遅い
大量のサンプルが必要でしたが、その場合計算が遅くなります。
というように、完璧な指標ではありませんが、人間の判断とある程度近い指標を利用することにより一定の評価ができるようになります。
Inception ScoreやFIDだけで判断するのは危険ですので、それ以外に人間の目で確認するなどが必要になります。
まとめ
今回はFIDについて簡単に見てみました。
他にもPrecision/RecallやHYPE(Human eYe Perceptual Evaluation)などがありますので、また機会があれば見ていきたいと思います。
では!
