今回は、BERT や GPT3 などの言語モデルを評価する際に一般的に利用されている perplexity (パープレキシティ)について解説したいと思います。
ここでは、厳密な説明というよりは直観的にわかりやすく、論文等を読んでいてぱっとイメージが湧くような説明をしたいと思います。
言語モデルとは
まず、言語モデルとは、ざっくり言うと次にどんな単語が出現する?かという確率を計算するモデルのことを言います。
これではわかりにくいので簡単な例で見てみましょう。
例えば「私は 犬が 好き です」という文章があるとします。
そして、「私は 犬が 好き ( )」として、カッコの中に入る単語は以下のうちどれでしょう?という問題を考えます。

- 猫
- です
- 行った
- 丸い
- 犬
日本語がある程度わかっている人であれば、文法的にも意味的にも2の「です」を選ぶのではないでしょうか。
これは、「?」に入る可能性の高い単語を「です」と評価していると考えられます。
言語モデルというのは、このように次の単語やカッコの中に入る単語が何か?ということを機械学習で学習させたものです。
日本語をきちんと理解しているほど、もう少し難しい文章になっても、どの単語が出てくるかを正しく予測できると考えられます。
言語モデルの良し悪し
ではここで、どんな言語モデルが良いのか?という言語モデルの良し悪しを考えてみましょう。
例えば、上記の「私は 犬が 好き ( )」という例を確率で表すと以下のような感じになっているのではないでしょうか。
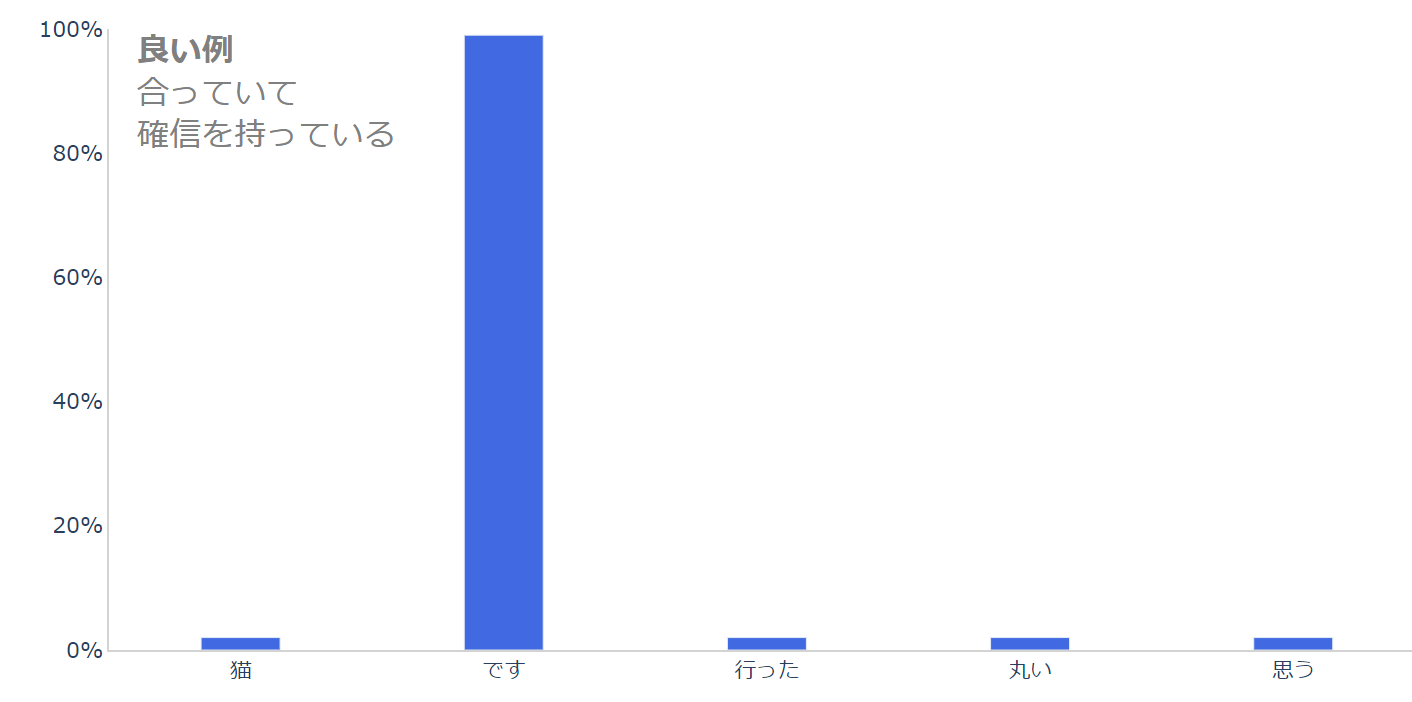
正しく、「です」を選び、かなり確信を持っています(「です」に確率が集中しています)。
一方で悪いモデルだとこんな感じになっているかもしれません。
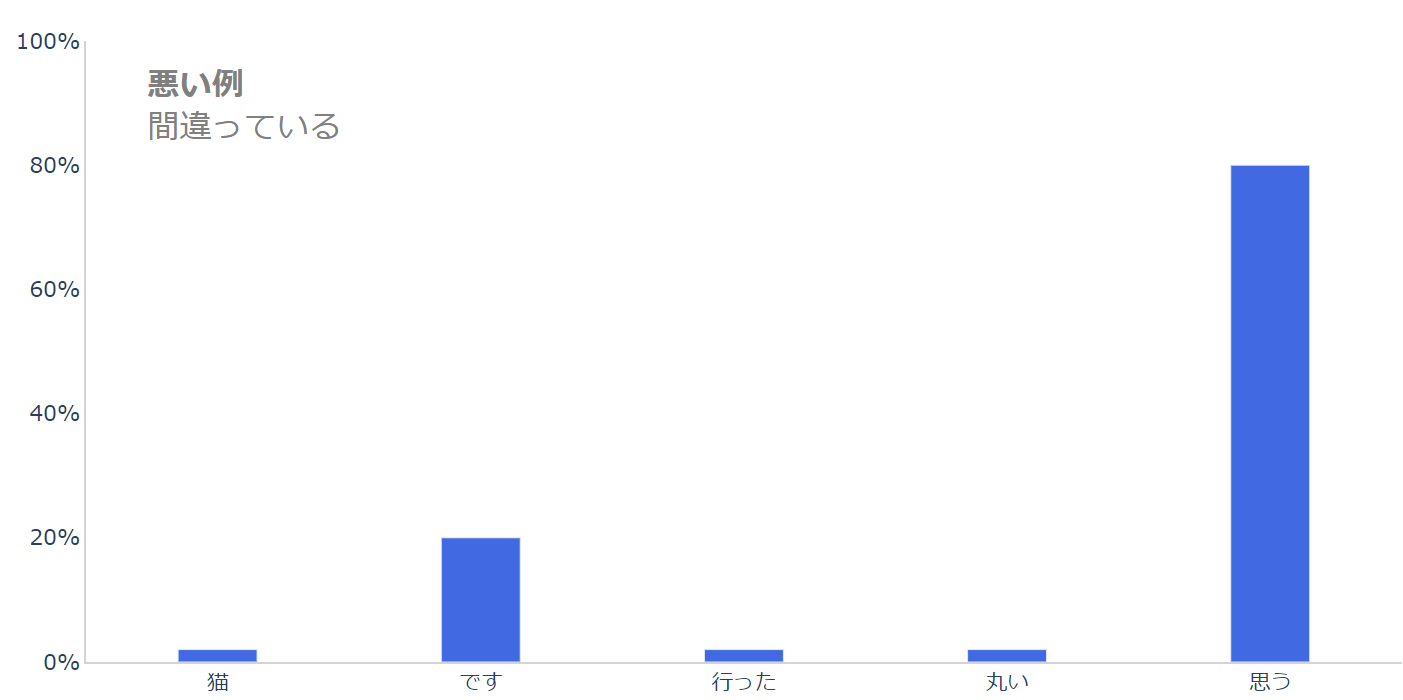
間違えて「思う」を選んでしまってますね。
人間でも、日本語がわかっていなかったり、すごく小さい子供であれば、このようになる可能性があり、言語モデルとしてはこれでは良くありません。
続いて、次の例は、正しく「です」を選んでいますが、あまり確信を持てていない場合です。
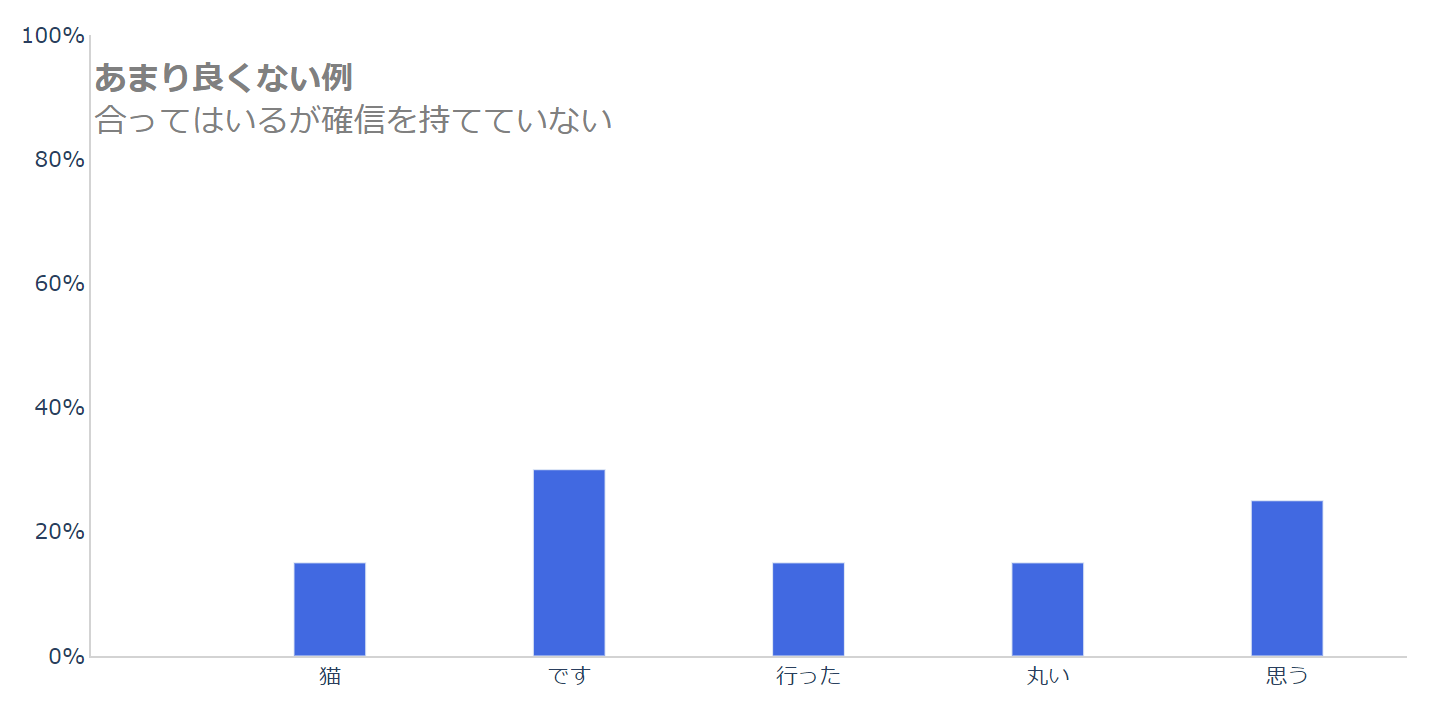
前の例よりはましですが、これもあまり良くありませんね。
この問題は人間にとっては非常に簡単な例なので、ちゃんと確信をもって、正解である「です」と答えてほしいところです。
以上から考えると、正しい単語の予測確率が高くなるような言語モデルが良いと考えられます。
perplexityとは
では、ここから本題の perplexity について説明します。
perplexity は、上記のように言語モデルの良い・悪いというものを機械的に評価する指標です。
上記の感覚的な説明のように、正しい単語を正しく予測していれば小さくなる指標です。
まず、たくさんの文章からなるデータセットがあるとします。
詳細の説明はのちほどしますが、そのときの perplexity は以下の式で計算できます。
$$\text{ppl}=\exp\left(-\frac{1}{N}\sum_{n}\sum_k t_{n,k}\log p_\text{model}(y_{n, k})\right)$$
ややこしくてわけがわかりませんね。
これからこの式の意味を少しずつ説明していきます。
とりあえず記号の意味ですが、\(n\) はデータセット中の \(n\) 番目の単語を表します。
\(t_{n, k}\) は \(n\) 番目の単語の正解ラベル (one-hot エンコーディングされているので、単語のリストである辞書の中の正解ラベルに対応する単語が1、それ以外はゼロ)、\(p_\text{model}(y_{n, k})\) は \(n\) 番目の単語に \(k\) を予測する確率を表します。
\(n\) 番目の正解の単語が「です」の場合、「です」のインデックスが105だとすると、\(t_{n,k}\) は以下のように \(t_{n, 105}\) だけが1で、それ以外は0になります。
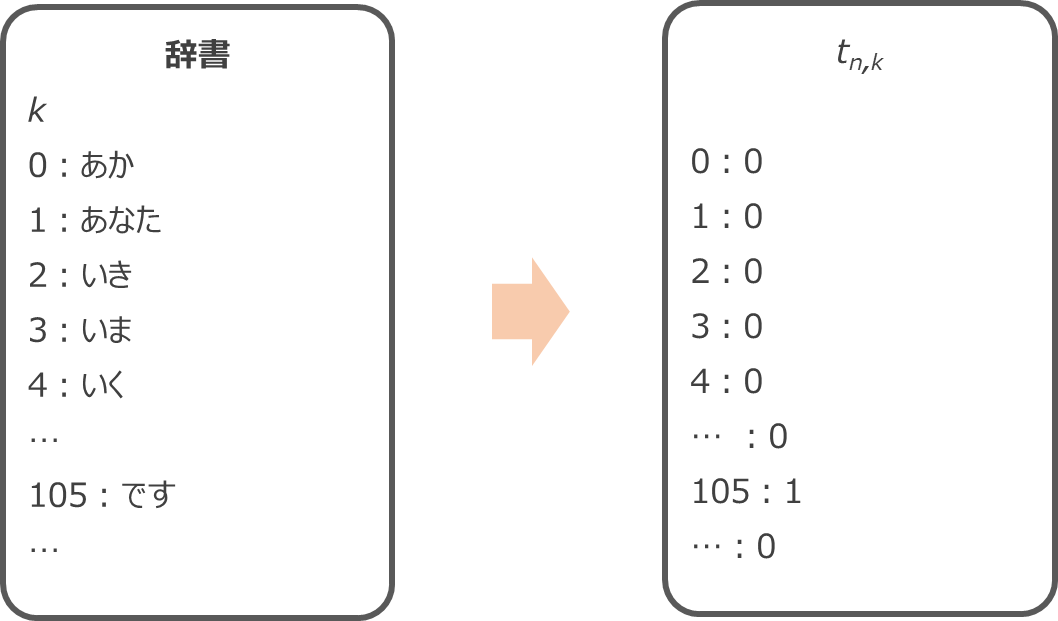
これを踏まえて、上記の式をもう少しわかりやすく書くと、
$$\text{ppl}=\exp\left(-\frac{1}{N}\sum_{n} \log (\text{正解となる単語の予測確率})\right)$$
と表されます。
つまり、log の中身は、正解となる単語、先ほどの例の場合だと「です」のモデルによる予測確率になります。
log の中身は正解となる単語をどれぐらい確信をもって予測しているか?
つまり、正しい答えを予測する確率が高いほど log の中身は大きくなります。
N分の1しているのは、すべての単語の平均を取っているということです。
ただ、この式だと perplexity がどういうものか直観的には理解できないので、少し単純化して見てみましょう。
1つの単語で考える
1つの単語について見ると、\(N=1\) なので
$$\begin{align}
\text{ppl}&=\exp\left(-\log (\text{正解となる単語の予測確率})\right)\\
&=\frac{1}{\text{正解となる単語の予測確率}}
\end{align}$$
となります(\(e\) の肩に \(log\) が乗っていると、\(log\) の中身になります)。
つまり、正しい単語の予測確率の逆数となります。
上記の例だと、「です」の予測確率なので、100%自信を持って「です」と予測する場合は perplexity が1になり、1%しか自信がなければ perplexity は100になります。
まんべんなく20%と予測していると perplexity は1÷0.2=5となります。
このことからも、正しい単語を自信を持って予測している場合 perplexity は小さくなるので、perplexityは小さいほどよい指標であることがわかりますね。
さらに、perplexity が1ということは、予測確率が100%なので「です」という単語1択に絞られていると解釈することができます。
perpleity が2 (予測確率が50%) ということは、2回に1回は正解ラベルを当てることができ、残りの1回は他のラベルを選択することを意味していますので、2個の選択肢に絞られていると解釈できます。
予測確率が10%の場合は perplexity が10なので、10個の選択肢に絞られていると考えることができます。
ということから、perplexityは “分岐数” と呼ばれることがあります。
直観的には perplexity の数値は次の単語がいくつの選択肢に絞られているか、を表す。
perplexty の最小値は1つの単語に絞られている場合の1になり、モデルが悪くなるにつれ大きくなっていきます。
単語列で考える
実際は一つの単語について perplexity を評価するのではなく、データセット中の大量の文章に対して perpleixty を計算します。
複数の文章について、前から順番に単語を予測していき、perplexity を計算します。
そして、全部で \(N\) 個の単語が存在する文章群の場合、各単語の perplexity の平均を取るだけです。
$$\text{ppl}=\exp\left(-\frac{1}{N}\sum_{n} \log (\text{正解となる単語の予測確率})\right)$$
厳密には exponential を取るタイミングにより1つの単語の perplexity の平均にはなっておらず、exponential の中身を平均しています。
(exponential は水準を調整するために使っているので、先に平均を計算しています)
以上が perplexity の直観的な解釈になります。
ちなみに、以下のように書くと、\(L\)はクロスエントロピー誤差なので、クロスエントロピー誤差に exponential を取ったものと考えられます。
$$\begin{align}
\text{ppl}&=\exp (L)\\
L&=-\frac{1}{N}\sum_{n}\sum_k t_{n,k}\log p_\text{model}(y_{n, k})
\end{align}$$
つまり、誤差が大きいほど perplexity も大きくなります。
まとめ
今回は言語モデルの評価指標である perplexity について見てきました。
情報理論の観点から見ると、もっと奥の深い話にはなってくるのですが、使う上では上記のような解釈で十分かなと思います。
今回の記事は、以下の本を参考にしておりますので、興味のある方はご参照いただければと思います。
「ゼロから作るDeep Learning ❷ ―自然言語処理」
「深層学習による自然言語処理」
わかりやすさで言うと「ゼロから作るDeep Learning ❷ ―自然言語処理」の方がわかりやすいですが、下の「深層学習による自然言語処理」もしっかりと理解するには非常によい本だと思います。
では!