さて今回は、最近テーブルデータの予測においてKaggleでもよく使われているTabNetの解説をしたいと思います。
このサイトでは自然言語処理分野がメインで画像認識分野を少しという感じでしたが、テーブルデータについても面白い発展があるようですね。
以下は簡単にまとめたTabNetの特徴です。
- ディープラーニングをベースとしたモデル。
- 特徴量の選択や加工などの前処理が不要で、end-to-endで学習することができる。
- アテンション・メカニズムを使い、各決定ステップ(decision step)において使用する特徴量を選択する。
アテンション・メカニズムにより解釈性が向上し、重要な特徴量をうまく学習することができる。 - 全サンプル共通ではなくサンプルごとに重要な特徴量を選択する。
- いくつかの特徴量をマスクし、それを予測するという事前学習を行う。
特徴量の選択が不要で、自動的に、しかも全体ではなくサンプルごとに重要な重要な特徴量を選択する、解釈性も高い、事前学習も行うということで興味が湧きますね。
もちろん精度面においても、現在主流の勾配ブースティングなどを上回る結果が出ています。
では、論文をもとに仕組みを見ていきましょう。
論文はこちらです。
『TabNet: Attentive Interpretable Tabular Learning』
論文とは説明の順序を少し変えていますのでご注意ください。
説明が長くなってしまい、一度読んだだけではわかりにくいかもしれませんが、何度か読んでいただけると整理されてくると思いますので、根気よく付き合っていただけると幸いです。
目次
TabNetの仕組み
では、TabNetの仕組みを見ていきましょう。
TabNetの概要
論文に沿ってTabNetのアイデアを説明します。
複数の決定ステップ(decision step)
以下の図はTabNetの処理イメージです。
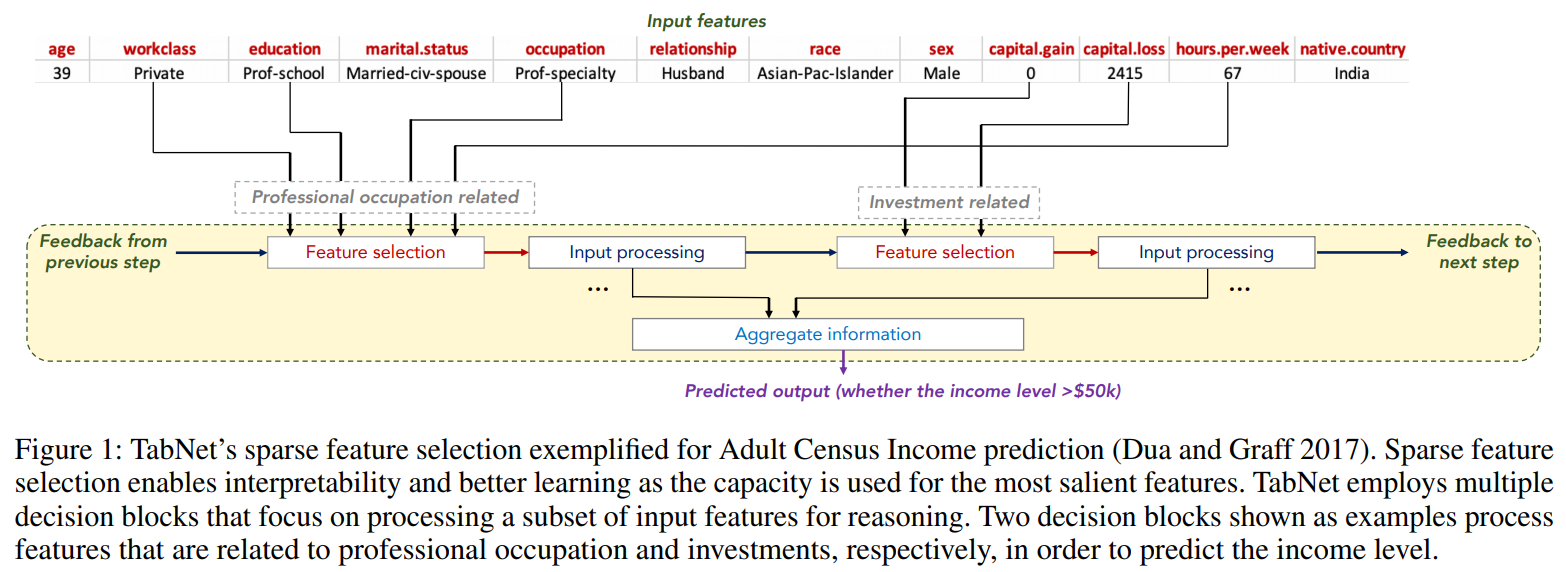
収入を予測するタスクの例ですが、上段がインプットとなっている特徴量、下段が処理の内容です。
TabNetは複数の意思決定ステップ(decision step)から構成され、前のdecisionステップからのフィードバックをもとに、次のステップで使う特徴量を選択し、その特徴量を処理していきます。
これを次のステップ、次のステップと繰り返していきます。
例えば上の図では、一つ目のdecisionステップにおいてはworkclass、educationといった職業・経歴に関する特徴量が選択されており、2つ目のdecisionステップでは、capital_gainなど投資に関する特徴量が選択されています。
このように、各意思決定ステップでデータをもとに自動的に特徴量を選択し処理するというのがTabNetの大きな特徴です。
ディープラーニング(Deep Learning) + 決定木(Decision Tree)
TabNetはベースはディープラーニングですが、そこに決定木(Decision Tree)の考え方を組み合わせます。
例えば、以下の左図のようにディープラーニングの形ですが、そのインプットである特徴量にマスクをすることで決定木の考え方を組み合わせることができます。
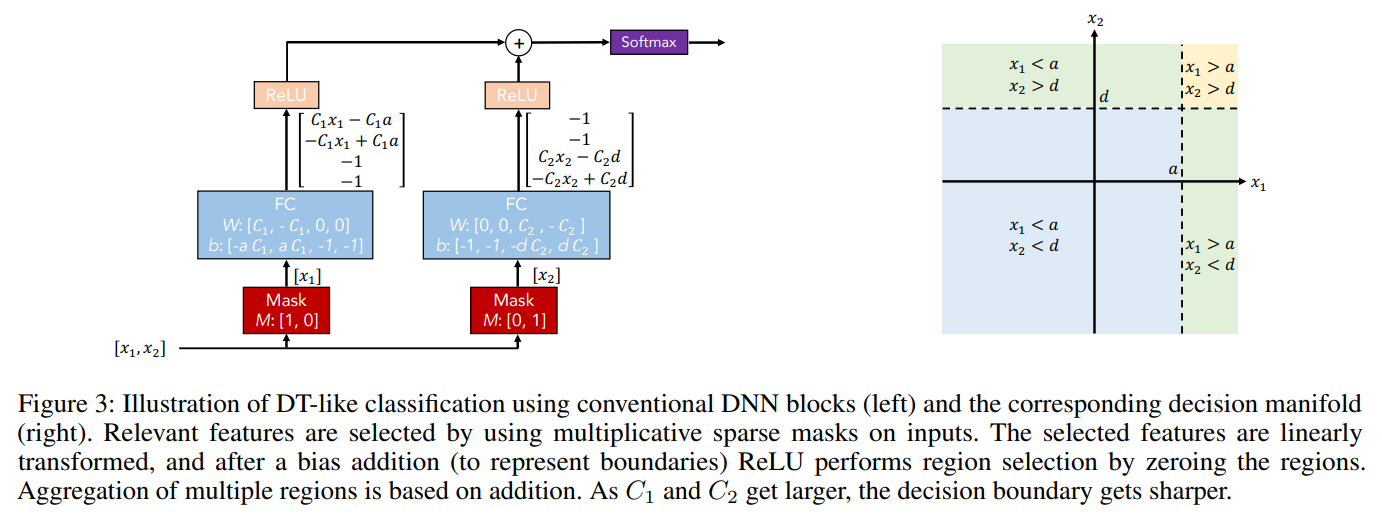
インプット\(x_1\)、\(x_2\)に対し、マスクをすることで特徴量を選択します。
例えば左側の1つ目のステップでは\(x_1\)だけを使うようにし、右側の2ステップ目では\(x_2\)のみを使うようにマスクをしています。
そして、全結合層のあとにReLUを適用し、その2つを結合してsoftmax関数を適用します。
これにより、右図にある決定木のような決定境界となります。
このように決定木とディープラーニングを組み合わせることで勾配ブースティングなどのテーブルデータでは主流になっている決定木ベースのモデルの精度を超えることが可能です。
事前学習-ファインチューニング
事前学習とは、タスクを解くための学習の前に、前もって事前知識などを学習をするというものです。
自然言語処理では一般的になっており、例えば文書分類のラベル付きデータを教師あり学習する前に、Wikipediaなどのラベルのない文章データを使って言語の仕組みを学習しておくといったものです。
そして、事前学習を終えたら、分類用のレイヤーを追加し、解きたいタスクのラベル付きデータを使って教師あり学習をします。
この解きたいタスクのラベル付きデータを使った学習をファインチューニングと呼び、事前学習-ファインチューニングというステップを行うことで飛躍的に精度が向上しています。
自然言語処理にける事前学習-ファインチューニングの解説はこちらの記事『事前学習 – ファインチューニングを理解する』をご参照ください。
TabNetではその考え方をテーブルデータに適用します。
ちなみに、事前学習はラベルがないデータを使うので、教師なし学習(Unsupervised Learning)とも言われますが、実際には自分が持っているデータをラベルとして使って学習するので自己教師あり学習(Self-supervised Learning)とも言えます(どちらが正しい呼び方かは知りません)。
では、以下がTabNetにおける教師なしの事前学習から教師ありのファインチューニングの例です。
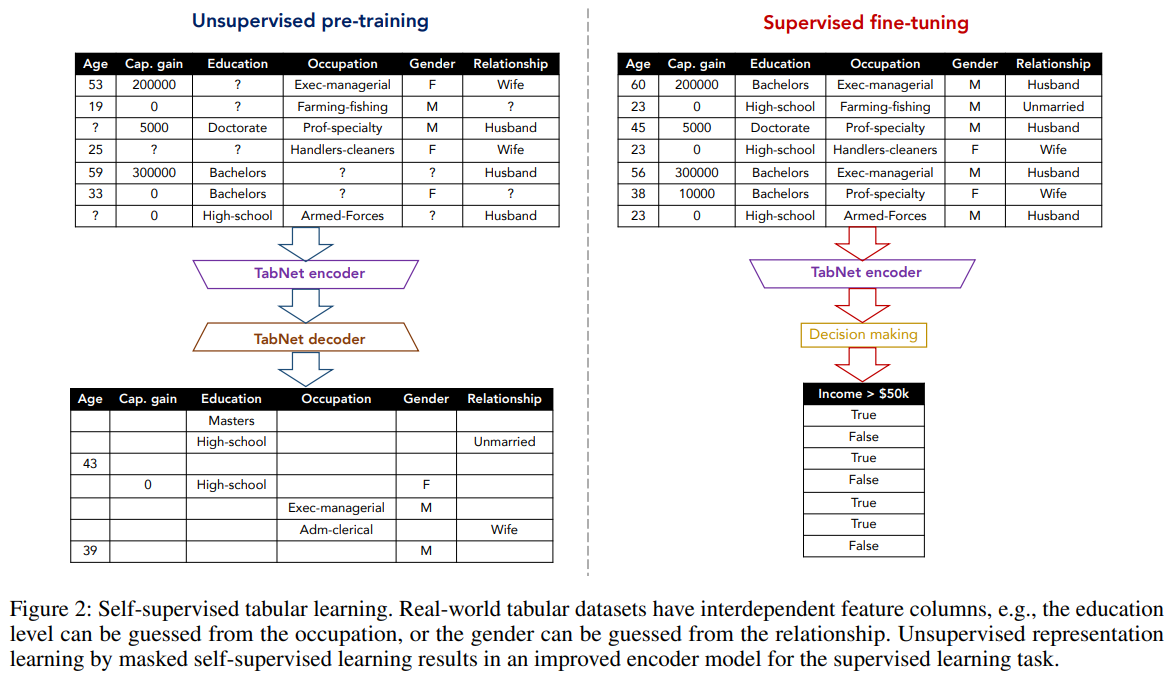
TabNetの教師なし学習(自己教師あり学習)では、各サンプルについてランダムに特徴量をマスクします。
例えば、左側の1行目のサンプルでは、Educationの値がマスクされており、それをTabNetエンコーダ、TabNetデコーダに通し、“?”になっていたEducationが何かを予測します。
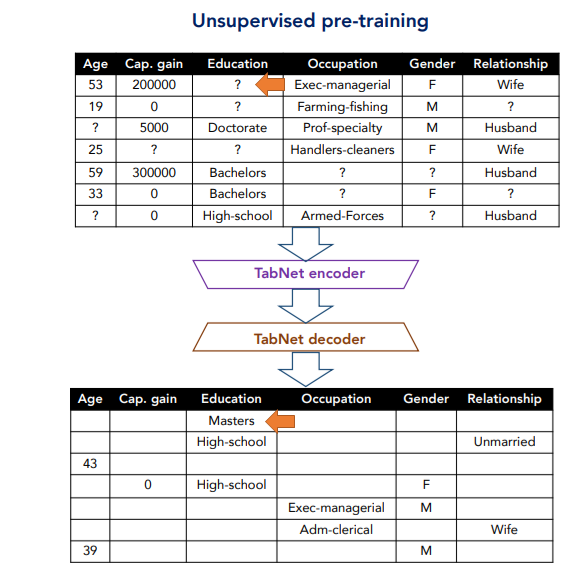
ここでは、答えはMastersです。
4行目のサンプルではCap. gainとEducationの2つがマスクされています。
TabNetの詳細
では、ここからはモデルの詳細について解説していきます。
TabNetの詳細を図で表したものが以下です。
といっても、なかなか簡単には解釈できないので、これからパーツごとに説明していきます。
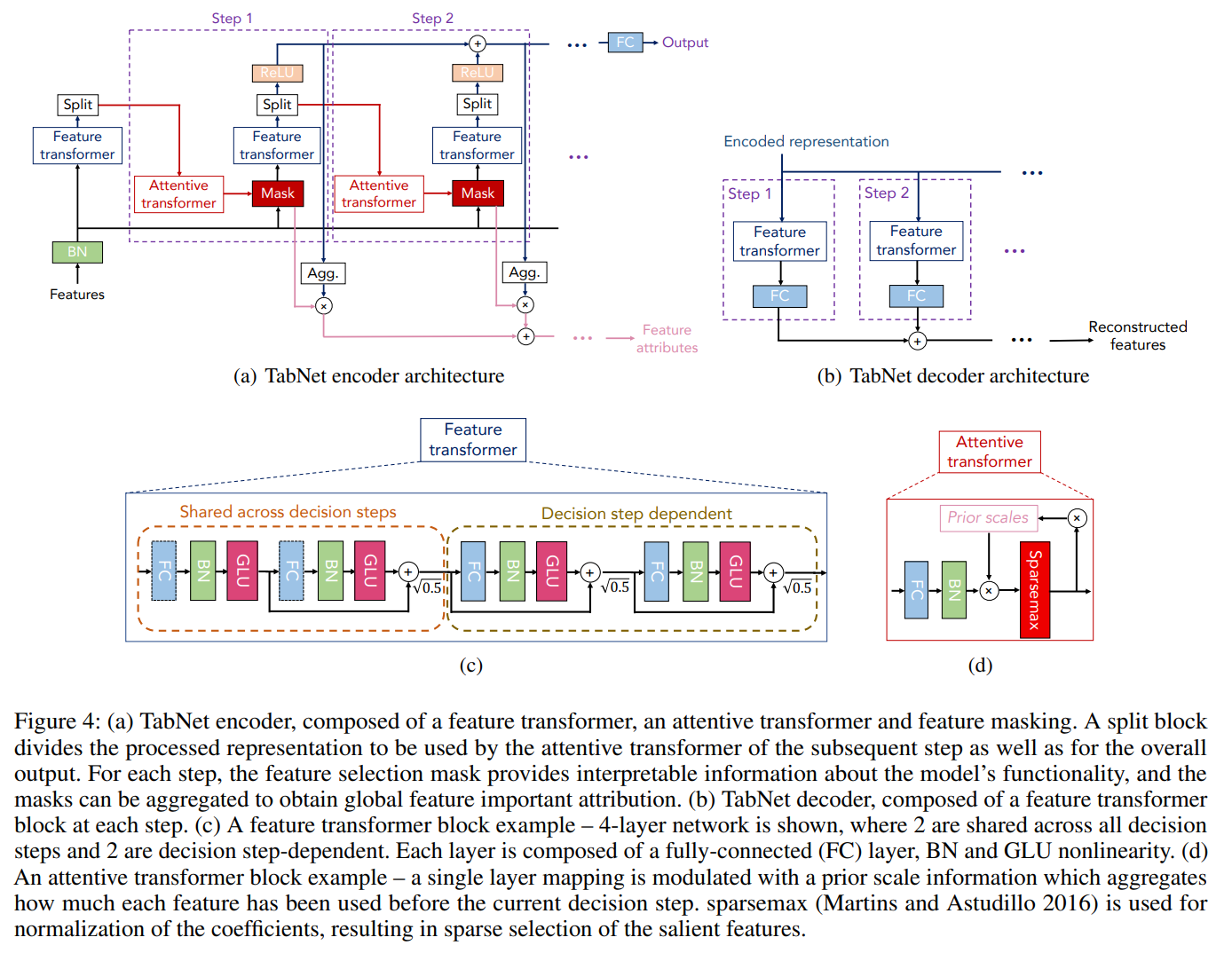
図は(a)から(d)のパーツに分かれていて、各図の意味は以下です。
- (a) エンコーダ
タスクの教師あり学習をする際の全体の構成です。大きくは、Feature TransformerとAttentive Transformerから構成されます。 - (b) デコーダ
事前学習をする際に使います。全結合層とFeature Transformerで構成されています。 - (c) Feature transformer
インプットされたマスク付きの特徴量を処理し、各ステップのアウトプットを計算します。2つのdecision stepの4つレイヤーで構成されます。 - (d) Attentive transformer
各ステップでサンプルごとにどの特徴量にフォーカスするかを決定します。Softmax関数ではなく、Sparsemax関数を使います。
(a)のエンコーダはTabNetの全体を表し、(c)のFeature transformerと(d)のAttentive transformerはそのエンコーダの一部のブロックになります。
では、順番に見ていきましょう。
まずは、全体像である(a)のエンコーダです。
(a) エンコーダ
エンコーダは実際にラベル付き学習をする際や推論をする際の仕組みです。
これをTabNetの仕組みと考えても問題ありません。
エンコーダの仕組みは以下のようになっています。
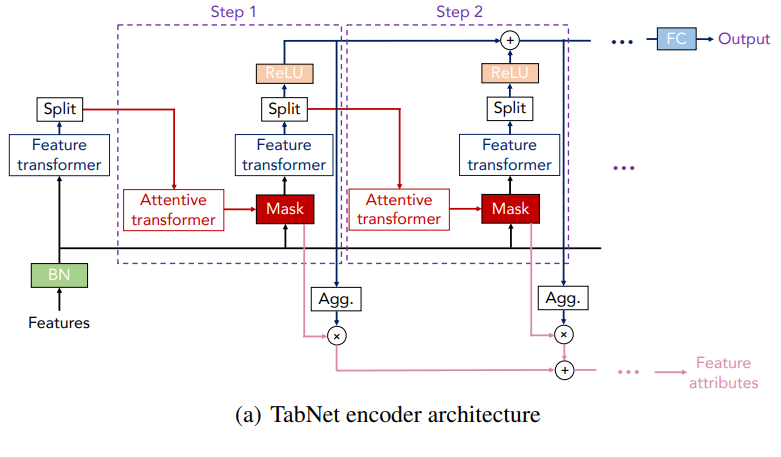
インプットの処理
まず、一番左のインプット部分を見ていきましょう。
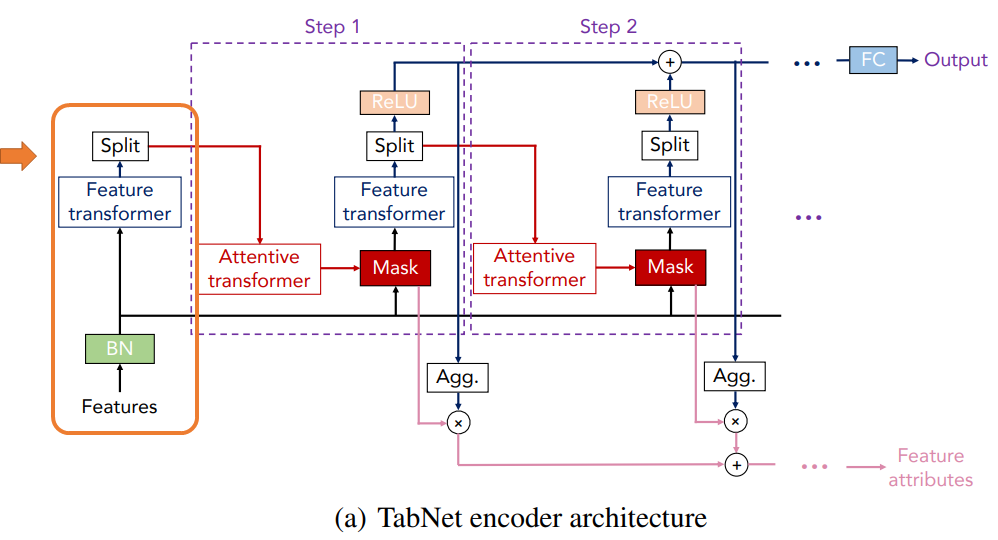
インプットは生の特徴量(Features)で、
「インプットの特徴量 → バッチ正規化 → Feature transformer → アウトプット」
という順番に処理をします。
まずインプットの特徴量を“BN”層でバッチ正規化(Batch Normalization)を行っています。
(バッチ正規化については『Batch Normalizationを理解する』で詳しく解説しています。)
そこから、“Feature transformer”でアウトプットを計算します。
“Split”という層はあとで出てきますのでここではいったん省略します。
この2つの仕組みはのちほど説明しますので、一旦、ここまではそういうものだと思っていただき、次のStep1に進みます。
続きのステップでは前のステップのアウトプットと生の特徴量をインプットとして、次で説明する処理を繰り返し行います。
Decisionステップの処理
では、Step1の処理を説明していきます(ただし、一般化するために\(i\)というステップを表す添え字も使用しています)。
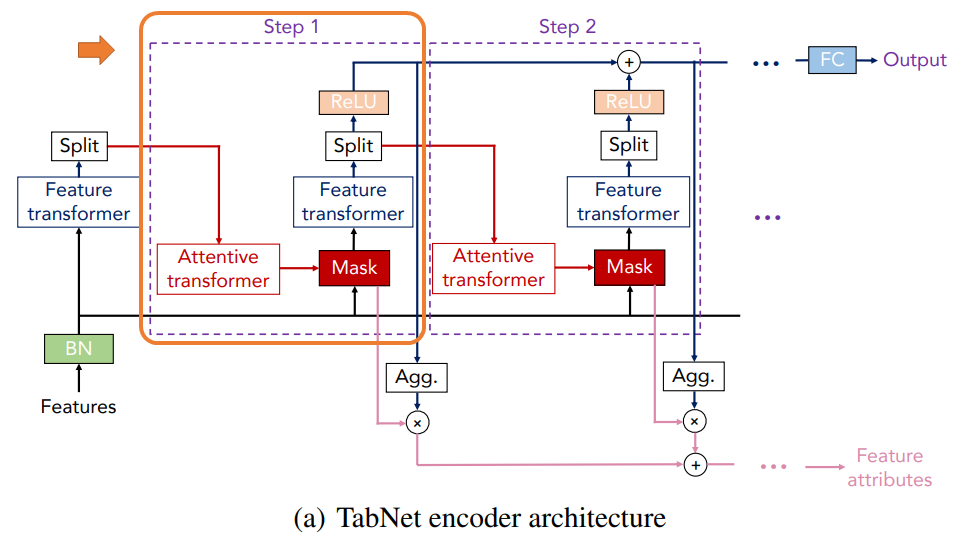
まず、前のステップのアウトプットを“Attentive transformer”というブロックに通します。
詳細はのちほど説明しますが、Attentive transformerブロックではどの特徴量が重要か?という情報を取り出し、そのステップにおいて使用する特徴量を選択します。
そして、その選択された特徴量に対してマスクをします。
\(i\)ステップ目のマスクを\(M[i]\in \mathbb{R}^{B\times D}\)とします。
\(B\)はバッチサイズで\(D\)はインプットする特徴量の次元です。
例えば、バッチサイズが3で特徴量が4つであれば以下のような3x4の行列になります。
$$\begin{align}
M[i]=\left[\begin{array}{cccc}0.0&0.2&0.8&0.0\\
0.1&0.0&0.0&0.9\\
0.2&0.6&0.2&0.0\end{array}\right]
\end{align}$$
各行の合計は1になるようになっています。
1つ目のサンプルに対するAttentive transformerの出力は[0.0, 0.2, 0.8, 0.0]というようになっており、0となっている特徴量はそのステップでは使用されません。
この値が1に近いほど、その特徴量は多く使われるイメージです。
(正規化された)\(f\)を生の特徴量とすると、マスクを要素ごとに掛け合わせた\(M[i]\cdot f\)が実際に使用する特徴量になります。
特徴量を薄めたり濃くしたりするイメージですね。
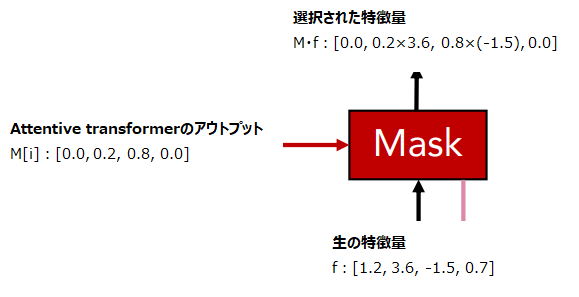
そして、これを“Feature transformer”ブロックにインプットし、特徴量を処理します。
Feature transformerブロックの詳細は次で解説します。
そして、Feature transformerブロックのアウトプットを“Split”という層で以下のように\(d[i]\)と\(a[i]\)の2つに分けます。
$$\left[d[i], a[i]\right]=f_i(M[i]\cdot f)$$
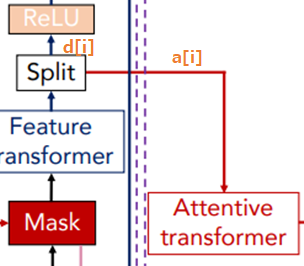
\(f_i\)が\(i\)ステップ目のFeature transformerの処理です。
2つに分けたうちの一つの\(a[i]\in \mathbb{R}^{B\times N_a}\)は次のステップのインプットとします。
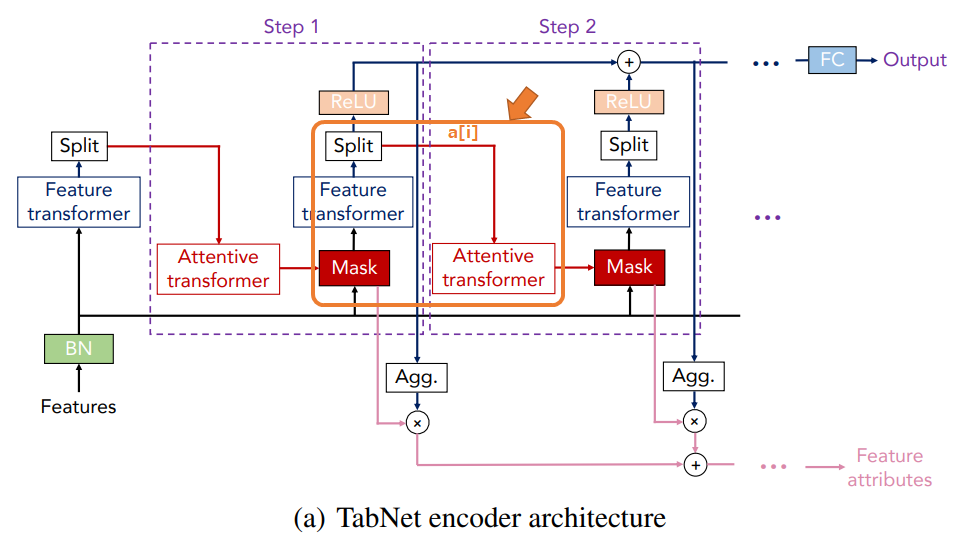
もう1つの\(d[i]\in\mathbb{R}^{B\times N_d}\)は、活性化関数ReLUを通し、その上で最終的なアウトプットを計算するために使います。
少しややこしいですが、\(d[i]\)はさらに2つのアウトプットを計算するために使われ、そのうちの1つは以下の部分のように最終的な推論をするために、各ステップの\(d[i]\)を足し上げて、全結合層で処理をします。
$$d_{out}=\sum^{N_{steps}}_{i=1}\text{ReLU}(d[i])$$
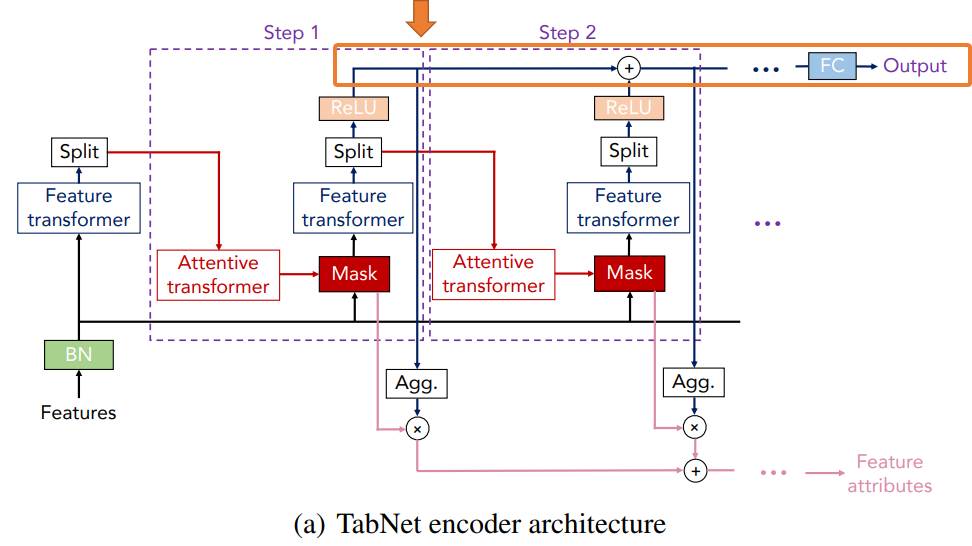
この\(d_{out}\)をdecision embeddingと読んでいます。
\(d[i]\)のもう一つ使い道は、特徴量の重要性を測ることです。
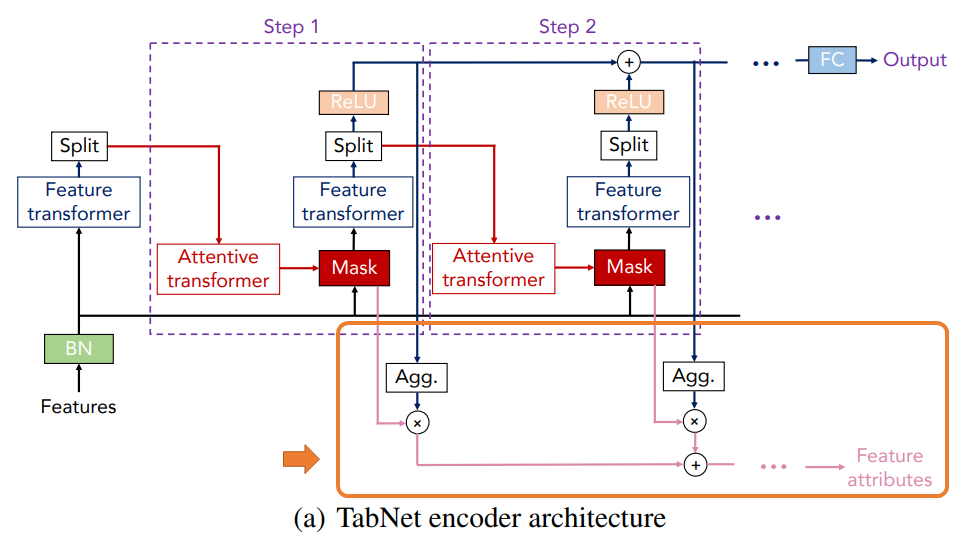
これについては、後程詳細を説明します。
ここでdecisionステップの処理をざっくりまとめておきます。
- Attentive transformerで注意を向ける先を決め(処理の詳細はのちほど)、それがマスク\(M[i]\)で表される。
- 生の特徴量\(f\)とマスク\(M[i]\)を掛けて、それをFeature transformerのインプットとして処理をする。
- Feature transformerで処理をしたアウトプットを\(a[i]\)と\(d[i]\)の2つに分ける。
- \(a[i]\)は次のdecisionステップに渡す。
- \(d[i]\)には2つの用途で使用する。
- 最終的な予測するために各ステップの\(d[i]\)を足し上げdecision embeddingを求め、全結合層で処理をする。
- 特徴量の重要性を測る。
(c) Feature Transformer
では、続いてTabNetを理解する上で重要な仕組みであるFeature transformerについて見ていきましょう。
Feature transformerブロックは特徴量を処理し、次のステップに流す情報や最終的な予測結果を出力するための情報を計算します。
ですので、一番重要な層と言えるかもしれません。
Feature transformer層は大きく2つの部品から構成されます。
- すべてのステップでパラメータが共通の部品(Shared across decision steps)
- 上記に続く各ステップごとにパラメータが異なる部品(Decision step dependent)
パラメータを減らすために各ステップで共通の部分を導入しています。
そして、各部品はそれぞれ2つの「全結合層(FC)→バッチ正規化層(BN)→GLU層(GLU)」というレイヤーから構成されます。
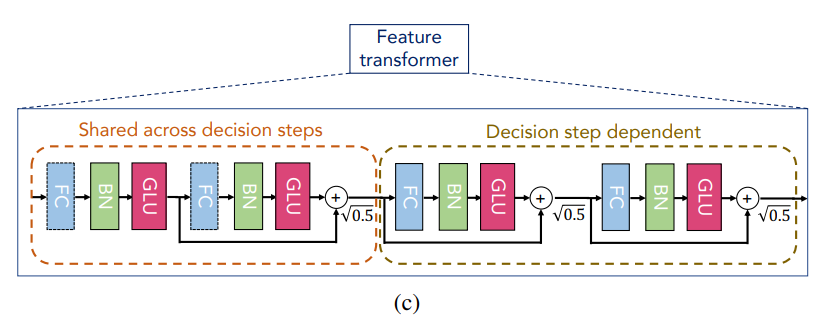
では、詳細を見ていきましょう。
パラメータが共通のステップ前半
まずは、すべてのステップで共通のパラメータからなる部品のうちの一つ目の層です。
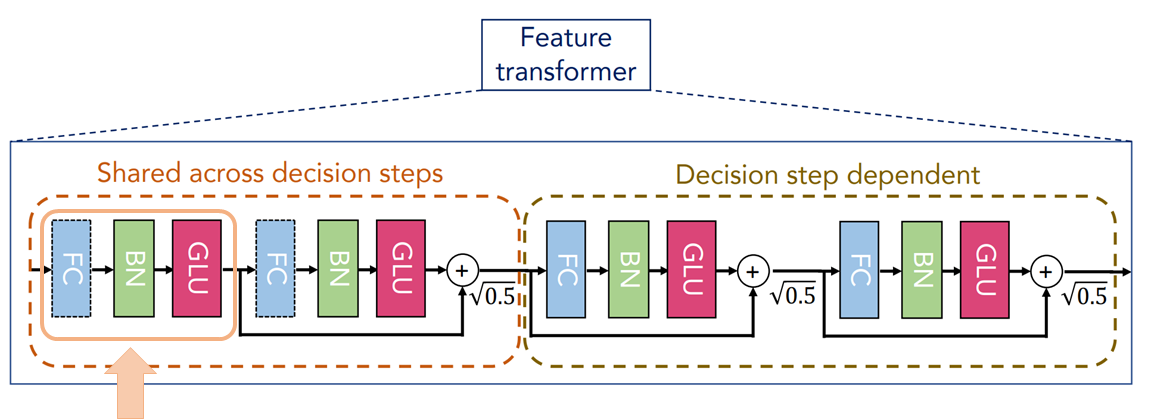
全結合層(FC)、バッチ正規化層(BN)ときて、最後に活性化関数GLU(Gated Linear Unit)で処理をします。
ここで、バッチ正規化と活性化関数GLUについて説明しておきます。
Ghost Batch Normalization
バッチ正規化はここではGhost Batch Normalizationという手法を使います(バッチ正規化の詳細については『Batch Normalizationを理解する』こちらをご参照ください)。
Ghost Batch Normalizationは『Train longer, generalize better: closing the generalization gap in large batch training of neural networks』で提案されたバッチ正規化の亜種です。
発想としては、収束を早くするためバッチサイズを大きくしたいのですが、単純にバッチサイズを大きくすると学習データの精度は改善してもテストデータの精度がそこまで改善しないという事象が見られます。
この差をgeneralization gap(汎化ギャップ)と呼びますが、これを改善するためにミニバッチをさらに小さな仮想的なバッチ(ghost batch)に分け、ghost batchごとにバッチ正規化を行うというものです。
なお、なぜこのようにすると汎化ギャップが改善するかということは論文には記載されていません。
アルゴリズムは次のようになっています。

詳細は割愛しますが、ポイントは以下のように
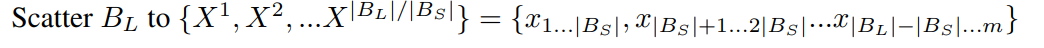
サイズが\(|B_L|\)のミニバッチをさらにサイズ\(|B_S|\)のghostバッチ\(X^1,X^2,\cdots\)に分割するところです。
そして、そのghostバッチごとに(移動平均で)平均・分散を計算して、ghostバッチごとに正規化しています。
TabNetの論文の1つの実験の設定を見ると、バッチサイズを\(B=3000\)として、ghostバッチのサイズを\(B_v=100\)としていますので、ミニバッチをさらに30のghostバッチに分けています。
また、このようにするのは学習時のみでテスト時は通常のバッチ正規化を行います。
GLU(Gated Linear Unit)
GLU層で非線形性が入ります。
GLU(Gated Linear Unit)は『Language Modeling with Gated Convolutional Networks』で提案された活性化関数で、
$$(X*W+b)\otimes \sigma(X*V+c)$$
で計算されます。
はじめの\((X*W+b)\)が次の層に流したい値で、インプット\(X)を線形変換したものになっています。(Linear)
\(\sigma(X*V+c)\)は0から1を取るので、その値をどれだけ流すか?を表します(\(\sigma(\cdot)\)はシグモイド関数)。
つまり、\(\sigma(X*V+c)\)が再帰的ニューラルネットワーク(RNN)などで良く出てくるゲートになっており(Gated)、1であればすべての情報を流し、0であれば何も流さない、0.5では半分程度を流す、というものです。
なのでGated Linear Unitという名前がついています。
なお、こちらの公式実装では、バイアスは省略し、\(W\)と\(V\)を結合した\(U\)を使って、
$$Y=X*U$$
として出力次元の2倍の大きさにし、その半分を流す情報に、残りの半分をゲートとして、
$$\text{GLU}=Y[:output\_dim]\otimes\sigma(Y[output\_dim:])$$
で計算しています(雑な数式ですみません…)。
そして、そのアウトプットを次の層に渡します。
パラメータが共通のステップ後半
次でも、同様に「全結合層→バッチ正規化層→GLU層」となっています。
基本的には前半と同じです。
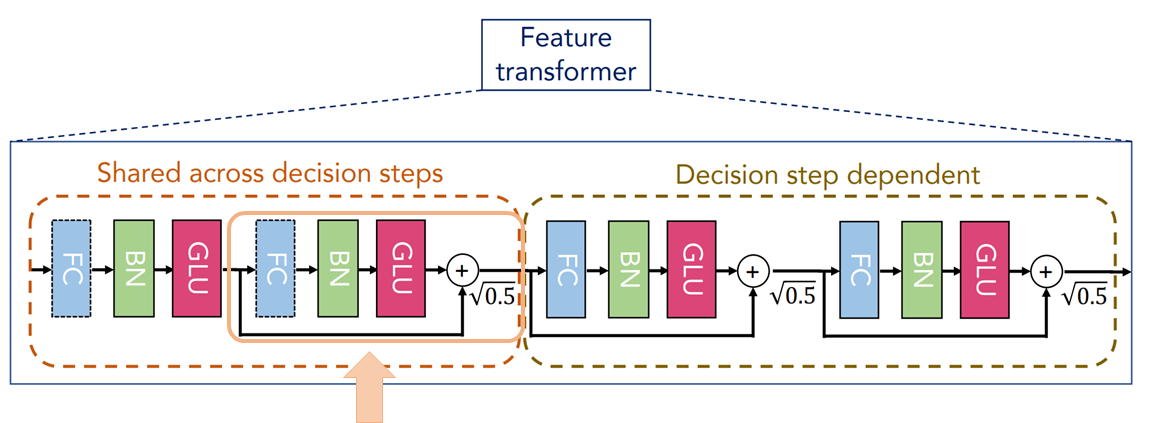
ただし、ここでは残差結合を適用します。
この層のアウトプットと前の層のアウトプットと足しています。
簡単に書くと
$$o + g(o)$$
です。\(g\)がパラメータが共通のステップの後半部分の処理を表し、\(o\)は前半のステップのアウトプットを表します。
さらに\(\sqrt{0.5}\)を掛けて正規化することで学習を安定させるようです。
以上が、すべてのステップで共通のパラメータを持つ部分です。
パラメータが異なるのステップ
続いて、各ステップごとにパラメータが異なる部分に入ります。
ここについては、以下を見ていただければわかるように、「全結合層→バッチ正規化層→GLU層」に残差結合を行ってものが2回続きます。
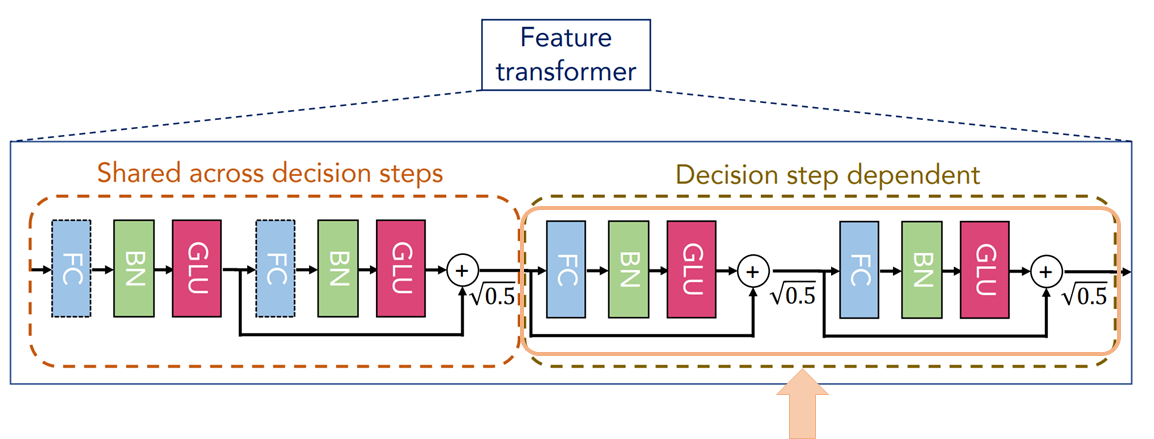
特に前の部分とあまり変わらないので説明は省略しますが、前の部分との違うところは各ステップごとにパラメータが異なるという点です。
(d) Attentive Transformer
では、続いてこちらもTabNetで重要なAttentive transformerブロックです。
Attentive transformerは重要な特徴量を選択するという役割を担っています。
以下のような仕組みです。
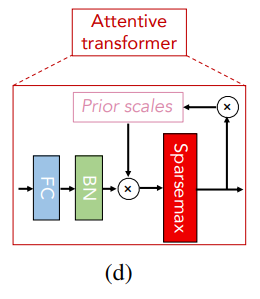
まず、attentive transformerブロックへのインプットを\(a[i-1]\in \mathbb{R}^{B\times D}\)としましょう。
\(a[i-1]\)は前のdecisionステップのアウトプットです。
全結合層、バッチ正規化層
まず、\(a[i-1]\)を全結合層(FC)、バッチ正規化層(BN)で処理をします。
ここのバッチ正規化層もghost batch normalizationを使っています。
\(a[i-1]\)に全結合層を適用することでどこに注意を向けるか?を計算するのですが、全結合層のパラメータを学習することで、どの部分が大事か?を学習します。
アテンション・メカニズムがわかっている方が理解しやすいのでこちらの記事『Attentionメカニズムを理解する』もご参考にしていただければと思います。
この2つの層の処理を関数\(h_i\)とすると、アウトプットが\(h_i(a[i-1])\)になります。
この\(h_i(a[i-1])\)にPrior scales \(P[i-1]\)を掛けます。
これについては後で説明しますのでいったん置いておきます。
Sparsemax関数
そして、その\(P[i-1]\cdot h_i(a[i-1])\)にsparsemax関数というsoftmax関数を改良したものを適用することで、どの特徴量を使うか?という0から1の間を取るマスク\(M[i]\)が求まります。
\(M[i]\)がゼロの特徴量は使われず、非ゼロの特徴量だけが使われます。
sparsemax関数はsoftmax関数と似ていますが、softmax関数がすべての候補カテゴリに対して確率非ゼロを割り当てるのに対し、sparsemax関数は一部については確率ゼロを割り当て、それ以外については非ゼロとなる関数です。
例えば10個のカテゴリがあるとsoftmax関数では以下のように1~10すべてのカテゴリに対し確率を割り当てるのに対し、
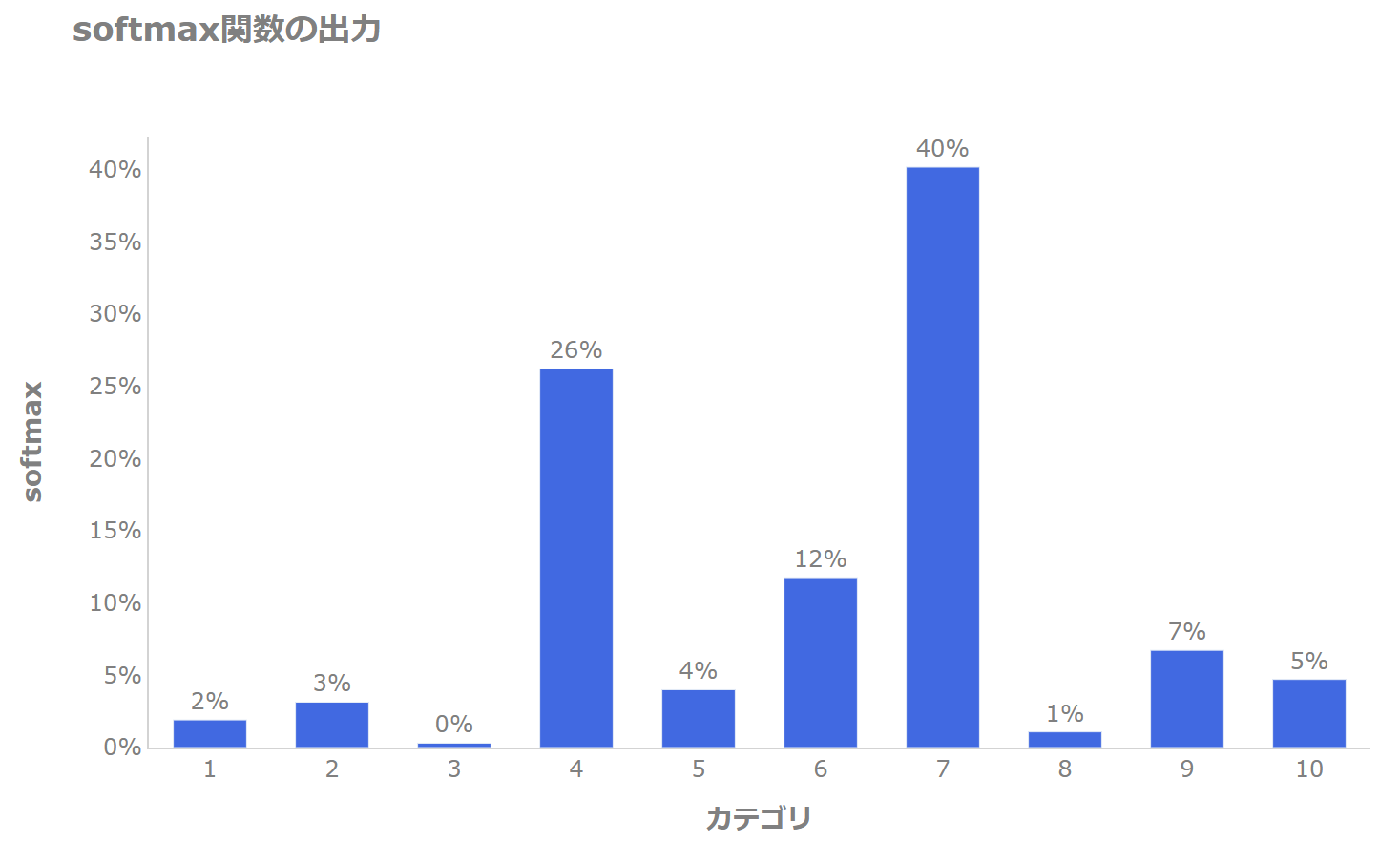
sparsemax関数では以下のようにカテゴリ特定のカテゴリ、この場合では4と7のカテゴリだけに確率を割り振り、それ以外については確率がゼロになります(スパース(疎)になります)。
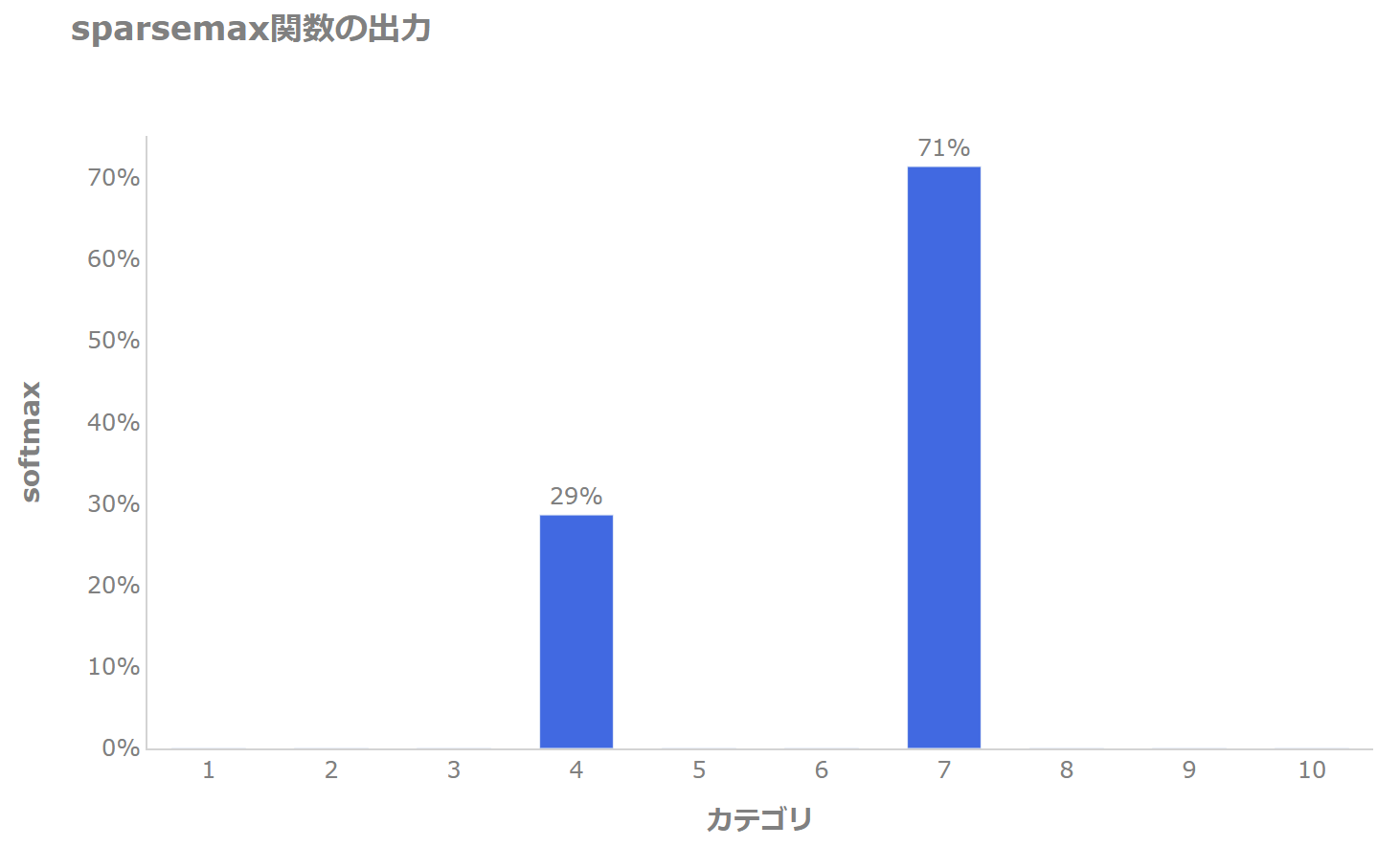
このようにすることで、特定の特徴量を使うように仕向けることを可能にします。
sparsemax関数の詳細については以下の記事をご参照ください。
これにより前の全結合層で求めたどこに注意を向けるか?を表す実数全体を取る数値を0から1の値に変換することができます。
例えば上記の図の場合だと、4つ目の特徴量は29%、7つ目の特徴量は71%使い、そしてそれ以外の特徴量はそのステップでは使わない、というイメージです。
Prior Scales
では、残っていたPrior Scales \(P[i]\)ですが、これは以下で表されます。
$$P[i]=\prod^i_{j=1}\left(\gamma -M[j]\right).$$
ここで、\(\gamma\ge 1\)はリラクゼーション・パラメータと呼ばれ、例えば\(\gamma=1\)であれば、
$$P[i]=\prod^i_{j=1}\left(1-M[j]\right).$$
となります。
\(M[j]\)は過去のステップのマスクで、各要素は0から1の範囲を取り、0であればそのステップではその特徴量は使われません。
例えば、仮にあるステップ\(i\)で1つの\(k\)番目の特徴量だけが使われる状態、つまり\(M_k[i]=1\)だったとしましょう。
その場合、上の式を適用すると\(i\)ステップ目以降のステップ\(j\)ではすべて\(P_k[j]=0\)になります。
それを\(h_i(a[i-1])\)に掛けることになるので、sparsemaxへのインプットは0になります。
そうすると、その特徴量は今後使われづらくなります。
それでも使われることがありますが、その場合\(P_k\)はマイナスになっていきますので、sparsemax関数ではさらに0が割り当てられる可能性が高くなってきます。
逆に\(\gamma\)を3とか5とか大きい数字にすると、一度使われても何度もその特徴量が使われることになります。
つまり、\(\gamma\)はその特徴量を使える容量みたいなもので、ざっくり言うと1つのステップだけしか使えなくするか、何度も使えるようにするか、というイメージです。
実験では\(\gamma\)は1.5や2.0といった値が使われています。
なお、\(P[0]={\bf{1}}^{B\times D}\)とします。
以上で、ステップ\(i\)でどの特徴量を重視するか?ということを決めることができるようになりました。
スパース性に対するペナルティ
1つのステップで、たくさんの特徴量を使うのではなく、より重要な特徴量に絞って使うようにすることを可能にすることを考えます。
ここでは、スパースにするために以下のような損失関数の項を追加します。
$$L_{sparse}=\sum^{N_{step}}_{i=1}\sum^{B}_{b=1}\sum^{D}_{j=1}\frac{-{\bf{M}}_{b, j}[i]\log\left({\bf{M}}_{b, j}[i]+\epsilon\right)}{N_{steps}\cdot B}$$
\(N_{steps}\)はdecisionステップの数、\(B\)はバッチサイズです。
\(M_{b,j}[i]\)は\(i\)番目のステップの\(b\)のバッチ、\(j\)番目の特徴量を表します。
マスクは各ステップ、各バッチ、各特徴量について適用されますので、すべてのマスクにおける各特徴量のマスクの合計をステップ、バッチで平均を取っています。
\(-x\log x\)は以下のような関数形なので、例えば0.4や0.5という中途半端な値を取ると\(L_{sparse}\)が大きくなります。
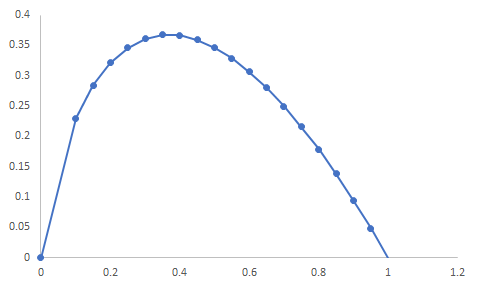
ですので、マスクを0や1といった値を取りやすくすることでスパース性をコントロールすることが可能です。
最終的な損失関数は
$$L + \lambda_{sparse} L_{sparse}$$
として、計算します。
\(\lambda_{sparse}\)はハイパーパラメータで、これが大きいほど非スパースなことにに対するペナルティが大きくなるので、より重要な特徴量のみが使用されるようになります。
実験では、\(\lambda_{sparse}\)は0.0001、0.01、0.005などが使われています。
解釈性
では、あるアウトプットが出力されたときに、どの特徴量が重要か?を説明する方法についてです。
一般にディープラーニングでは解釈性が低いことが問題になります。
例えば、よく出される例として、住宅ローンなどの申請を金融機関に行って、その結果、借入不可となった場合に金融機関は「なぜ借り入れができないのか?」を説明できる必要があります(申請者に説明する義務はありませんが、金融機関内部ではある程度説明できる必要があります)。
TabNetではattentionを使っているので、そこをある程度説明することが可能になります。
その説明のために、マスク\(M[i]\)を使います。
\(M_{b, j}[i]\)は\(i\)番目のステップにおける\(b\)番目のサンプルの\(j\)番目の特徴量のマスクを表します。
これが1に近いと\(j\)番目の特徴量が使われ、ゼロであれば使われません。
ただ、このマスクはステップごとに違います。
このマスクの値をステップごとに合計して正規化するというのも一つのやり方ですが、TabNetでは各ステップ自体の重要性も考慮します。
それが上記で詳細の説明を後回しにしたエンコーダの以下の部分です。

decisionステップの重要性
まず、\(b\)番目のサンプルの\(i\)番目のステップの重要性を、
$$\eta_{b}[i]=\sum_{c=1}^{N_d}\text{ReLU}(d_{b, c}[i])$$
とします。
\(d[i]\)は、ステップ\(i\)のFeature transformerブロックで処理された最終的な予測に使うための埋め込み表現でしたので、\(d_{b, c}[i]\)はステップ\(i\)における\(b\)番目のサンプルの\(c\)番目の次元の要素です。
例えば、\(b\)番目のサンプルのステップ\(i\)における埋め込み表現が以下のようになっています。
$$[-0.12, 0.22, -0.87, 1.2, ...]\in \mathbb{R}^{N_d}$$
これをReLUを通して、
$$[0, 0.22, 0, 1.2, ...]\in \mathbb{R}^{N_d}$$
として、各要素\(c\)について合計することで、\(b\)番目のサンプルにおける各\(i\)番目のステップの重要性が表されます。
なぜこれがステップの重要性を表すと考えられるかというと、最終的な予測に使う埋め込み表現は以下で与えられ、
$$d_{out}=\sum^{N_{step}}_{i=1}\text{ReLU}(d[i])$$
これを使って最終的な予測を行います。
つまり、\(d[i]\)がゼロ以下であればReLU関数によりゼロが設定され、予測に有用な値にはなりません。
なので、重要な情報はゼロ以上になるように学習します。
例えば、\(b\)番目のサンプルにおける各\(i\)番目のステップの埋め込み表現にあたる\(d_{b, c}[i]\)がすべて0よりも小さければ、そのステップでの埋め込み表現はすべてゼロになるので、\(d_{out}[i]\)の\(b\)番目の要素には貢献せず、大きい値をもつステップほど最終的な予測に貢献するということです。
ステップの重要性を考慮した特徴量の重要性
そして、このdecisionステップの重要性\(\eta_b\)も考慮して、最終的に特徴量の重要性を以下で表します。
$$M_{agg-b,j}=\frac{\sum^{N_{steps}}_{i=1}\eta_b[i]M_{b,j}[i]}{\sum^D_{j=1}\sum^{N_{steps}}_{i=1}\eta_b[i]M_{b,j}[i]}$$
基本的には\(M_{b,j}\)が\(b\)番目のサンプル、\(j\)番目の特徴量の重要性を表しますが、これにそのサンプルについての各ステップの重要性\(\eta_b\)で重みづけをしています。
分母は特徴量で合計を取っていますので、\(M_{agg-b,j}\)は各特徴量の相対的な重要性になります。
事前学習 - テーブル自己教師あり学習(Tabular self-supervised learning)
最後に事前学習についてです。
前述の通り、TabNetの事前学習は以下のようにサンプルごとにランダムに特徴量をマスクし、それを他の特徴量から予測するものです。
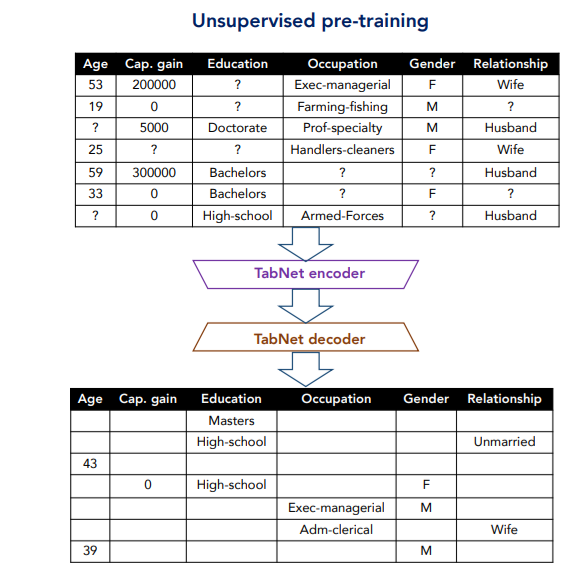
ここで、TabNet encoder、TabNet decoderとありますが、前述の(a)エンコーダで特徴量を処理して埋め込み表現\(d_{out}\)に圧縮し、圧縮した情報をデコーダでもとに戻すイメージです。
このマスクされた部分を予測するように学習することで、各特徴量の関連性などを学習することができます。
インプットの特徴量を\(f\)とすると0か1のマスク\(S\in \{0, 1\}^{B\times D}\)を使って\((1-S)f\)をエンコーダのインプットとします。
\(S_{b, j}=1\)であればマスクをするのでインプット\((1-S_{b,j})f_{b,j}\)はゼロになります。
そして、デコーダで予測したものが\(S\cdot\hat{f}\)です。
エンコーダは既に説明した以下の部分になりますので、このアウトプットに対して前述のFeature transformerと全結合層を適用し、足しこむことで特徴量を再構築するように学習します。
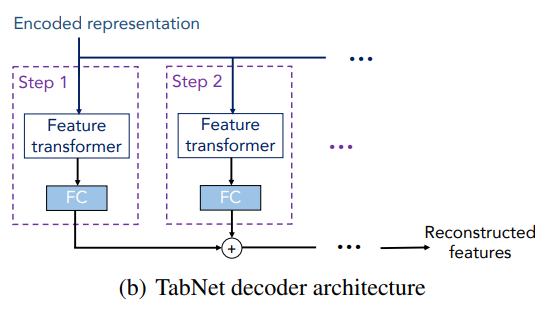
再構築誤差(reconstruction error)は以下とし、この再構築誤差を小さくするように学習します。
$$L_{reconstruct}=\sum^B_{b=1}\sum^D_{d=1}\left|\frac{\left(\hat{f}_{b,j}-f_{b,j}\right)\cdot S_{b,j}}{\sqrt{\sum^B_{b=1}\left(f_{b,j}-1/B\sum^{B}_{b=1}f_{b,j}\right)^2}}\right|$$
分母は標準偏差で正規化しているイメージです。
これを教師あり学習をする前に行い、事前に特徴量に関する知識を埋め込みます。
最終的には、事前学習により特徴量の関連性などを学習したあとに、ファインチューニングと呼ばれる教師ラベルを使った教師あり学習を行います。
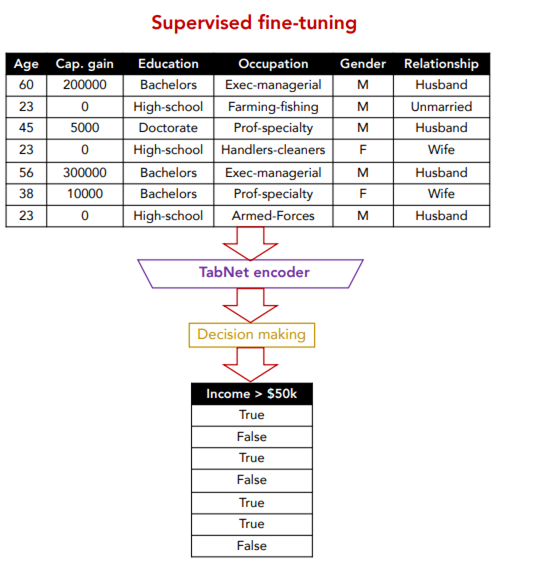
このときは学習したデコーダは使わずに捨てて、Decision makingという層を追加し、エンコーダで圧縮した情報を使ってDecision making層で分類タスクを学習します。
Decision makingとある層は一般的なロジスティック関数やsoftmax関数などです。
実験結果
さて、仕組みを見たところで実験結果を見ていきましょう。
実験方法
詳細は論文をご参照いただきたいのですが、実験に当たって重要な点は以下です。
- カテゴリ変数については、1次元の学習可能な埋め込み表現に変換します。
例えば、子供あり・子供なしという2つのカテゴリが合った場合、それぞれ1次元の数値に変換し、子供ありは4.3、子供なしは-0.8などと学習します。
次元を増やしてもいいのですが、各次元の意味を解釈できないため1次元にしているとのことです。 - 数値情報はそのまま入力とし、前処理は行いません。
これはTabNetでは前処理は不要という意味ではなく、行った方が精度が改善する可能性がありますが、この実験では行わないということです。
実験結果
では、実験結果を見ていきましょう。
サンプルごとの特徴量選択(Instance-wise feature selection)
1万学習サンプルからなる6つの手作りデータで確認します。
Syn1からSyn3のデータセットは重要な特徴量がすべてのサンプルで共通で、重要な特徴量はX3からX6になります。
つまり、これらのデータセットでは、サンプルごとに特徴量を変えないことで精度が改善します。
Syn4からSyn6はサンプルごとに重要な特徴量が異なり、例えば、X11の値によりX1からX2が重要か、もしくはX3からX6が重要かが変わるようなデータです。
この場合では、特徴量をあらかじめ選択するというのは最適ではなくなります。
以下がこれらのデータセットの実験結果で、各モデルのAUC(Area Under the Curve)が表示されています。
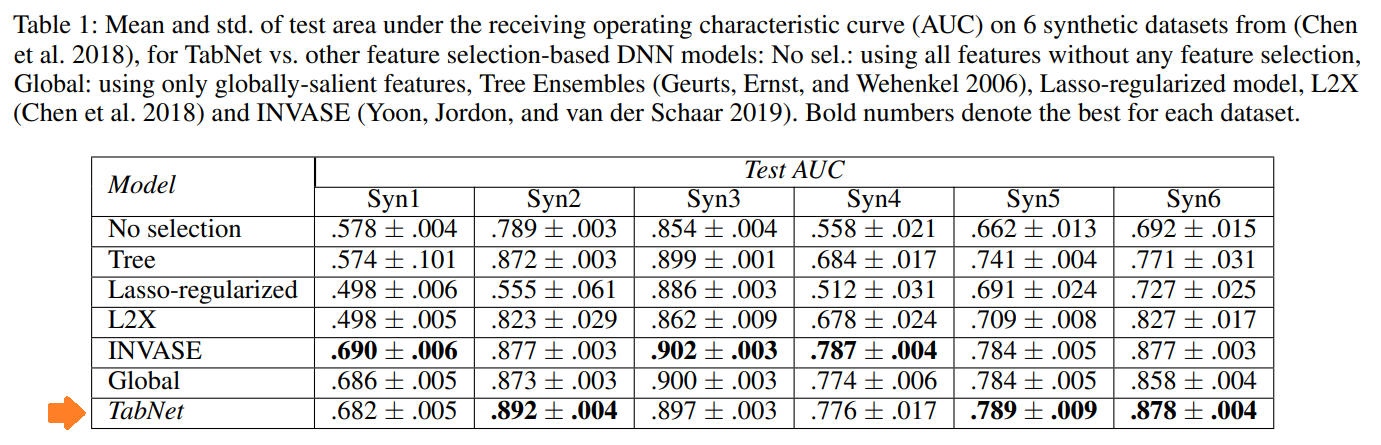
一番下がTabNetですが、まとめると以下になります。
- Treeベースのアンサンブル・モデル、Lasso、L2Xと比べるとTabNetがアウトパフォームしている。
- INVASEとはほぼ同等の精度。ただし、パラメータ数はINVASEが10万超なのに対し、TabNetは2万6千と大幅に少なく効率的である。
- Syn1からSyn3については、globalに特徴量を使用した場合と同等の精度だが、Syn4からSyn6については、サンプルごとに使用する特徴量を変えることができるTabNetがアウトパフォームしている。
Foreset Cover Type
上記は、手で作成したデータですが、実際のデータの結果を見てみます。
forest cover type(どんな木で覆われているか)を当てる分類タスクです。
結果は以下です。
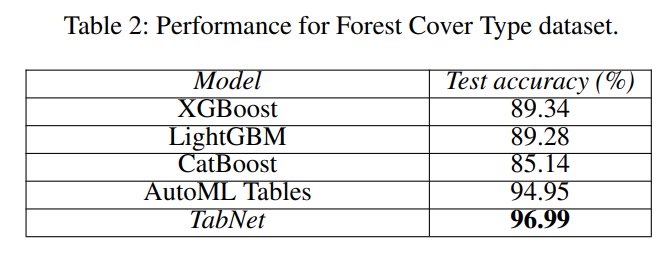
主流である勾配ブースティングを使った決定木ベースのモデルを大幅に上回っています。
AutoML Tablesとは差は大きくありませんが、それでも上回っています。
AutoML Tablesはハイパーパラメータを細かく分析して決めているのに対し、TabNetは細かいハイパーパラメータ・サーチは行っていません。
Poker Hand
次に、Poker Handデータセットというポーカーの手を当てるタスクです。
このタスクは、どのような手札になっているかという情報が与えられ、そこからワン・ペア、スリー・カードなどを当てるものです。
ルールベースであれば100%の精度が出ますが、極めて不均衡なデータのため機械学習では簡単ではありません。
結果は以下のようになっています。
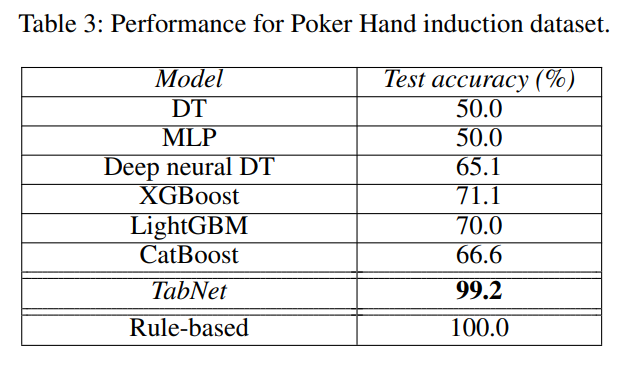
DT(決定木)やMLP(マルチ・レイヤー・パーセプトロン)の精度は低く、勾配ブースティングで70%前後です。
一方でTabNetでは99.2%という高精度が出ています。
解釈性
続いて精度ではなく、予測の理由を特定する解釈性を見てみましょう。
前述の通り、TabNetではアテンション・メカニズムを使っているため、どの特徴量をどれだけ重要視したか?ということがわかります。
ここでは、Attentive Transformerで計算したマスク\(M\)を使って重要度を可視化します。
以下がマスクの数値を可視化したものです。マスク\(M\)の値がゼロに近いほど黒く、1に近いほど白くなります。
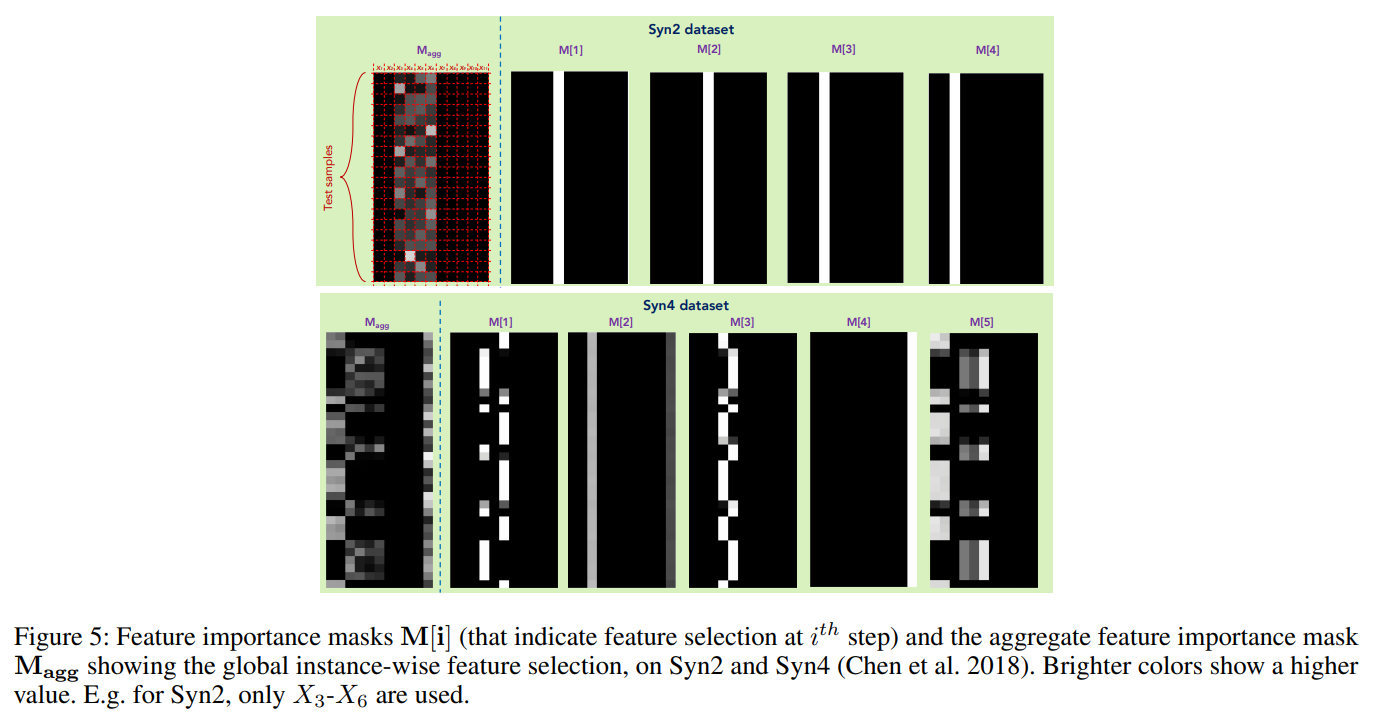
例えば、上段の図はSyn2データセットですが、これは全サンプルについてX3からX6の特徴量を使うことで精度が向上するデータセットです。
\(M[1]\)から\(M[4]\)までステップごとにそれぞれX3だったりX4だったりと違っていますが、X3からX6のどれかにに注意が向いていることがわかります。
一番左の\(M_{agg}\)を見ると、X3からX6のみに注意が向いていることがわかります。
つまり、サンプルごとに違いますが、予測で使われた特徴量は\(M_agg\)の大きさを見ることでわかります。
下段のSyn4データセットの結果では、\(M[1]\)ではX4とX6に注意が向いていますが、サンプルごとにどちらにどれだけ注意を向けるかが異なっています。
\(M_{agg}\)を見てみると、X11にも注意が向いており、サンプルごとにX11の値に応じてどの特徴量に注意を向けるかを学習していることがわかります。
事前学習の効果
TabNetでは事前学習を行うという特徴があります。
この効果を見るために、データセットの大きさを変えて、事前学習なし(Supervised)と事前学習あり(With pre-training)を比較しています。
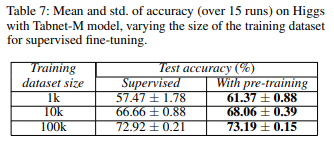
一番下の10万サンプル(100k)の場合、0.2%程度しか事前学習をすることで改善していませんが、一番上の1000サンプル(1k)の場合、事前学習により精度が4%程度も改善しています。
サンプルが少ないほど事前学習により精度がより大きく改善するという結果です。
以下の記事では自然言語処理で事前学習の効果を簡単に見ていますが、それと同じ結果になっています。
また、以下の図にある通り、事前学習あり(With pre-training, 青線)では事前学習なし(Supervised, 緑線)よりもかなり早く精度がピークに達しており、収束が早いことがわかります。
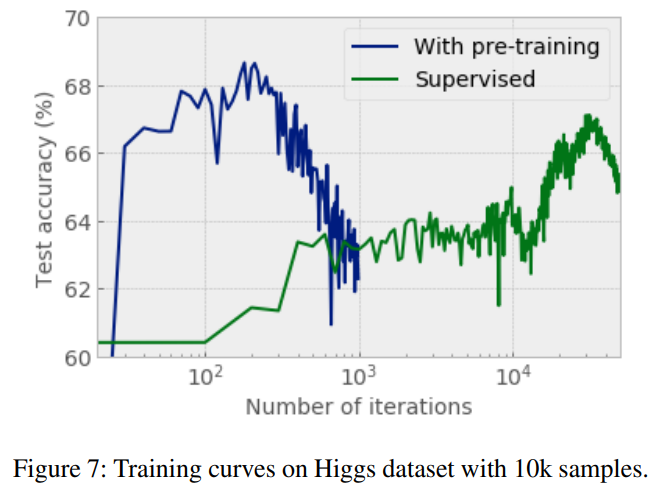
まとめ
今回は、テーブルデータでよく使われているTabNetを紹介しました。
自然言語処理では一般的になっているTransformer/Self-attentionという仕組みを使ったり、事前学習-ファインチューニングというステップをテーブルデータにも適用したりと非常に興味深い論文でした。
業務でも試してみたくなりますね。
論文には、他にも実験結果や各実験におけるハイパーパラメータの設定についても記載されています。
理解の助けになると思いますので、興味のある方は論文を読んでいただければと思います。
では、また!
