【解説+実装】Sparsemax関数を理解する

今回は、テーブルデータの処理で良好な結果を残しているTabNetなどで使われているSparsemax関数について解説したいと思います。

Sparsemaxは複数ラベルのある分類問題に通常使われるSoftmax関数を変形したものです。

どう変形したかというと、Softmax関数はすべてのラベルに対して確率を与えますが、Sparsemaxは一定のラベルに対しては確率が0となります。

つまり、その名の通りスパース(疎)な出力をするsoftmax関数ということです。

なお、この記事では、Sparsemaxの順伝搬についてのみ解説します。

逆伝搬時、つまりSparsemaxの勾配については触れませんが、こちらはそれほどややこしくないので必要に応じてSparsemax関数を微分して確認していただければと思います。

その他にも色々記載されていますので、興味がある方は論文を読んでいただければと思います。

論文はこちらになります。

From Softmax to Sparsemax: A Sparse Model of Attention and Multi-Label Classification

では、見ていきましょう。

1 Softmax関数
2 Sparsemax関数
- 2.1 Sparsemax関数のアルゴリズム
3 Sparsemax関数の理論
4 実装
5 まとめ

Softmax関数

まず、カテゴリが10個あり、$z$(logit)が以下で与えられているとします。

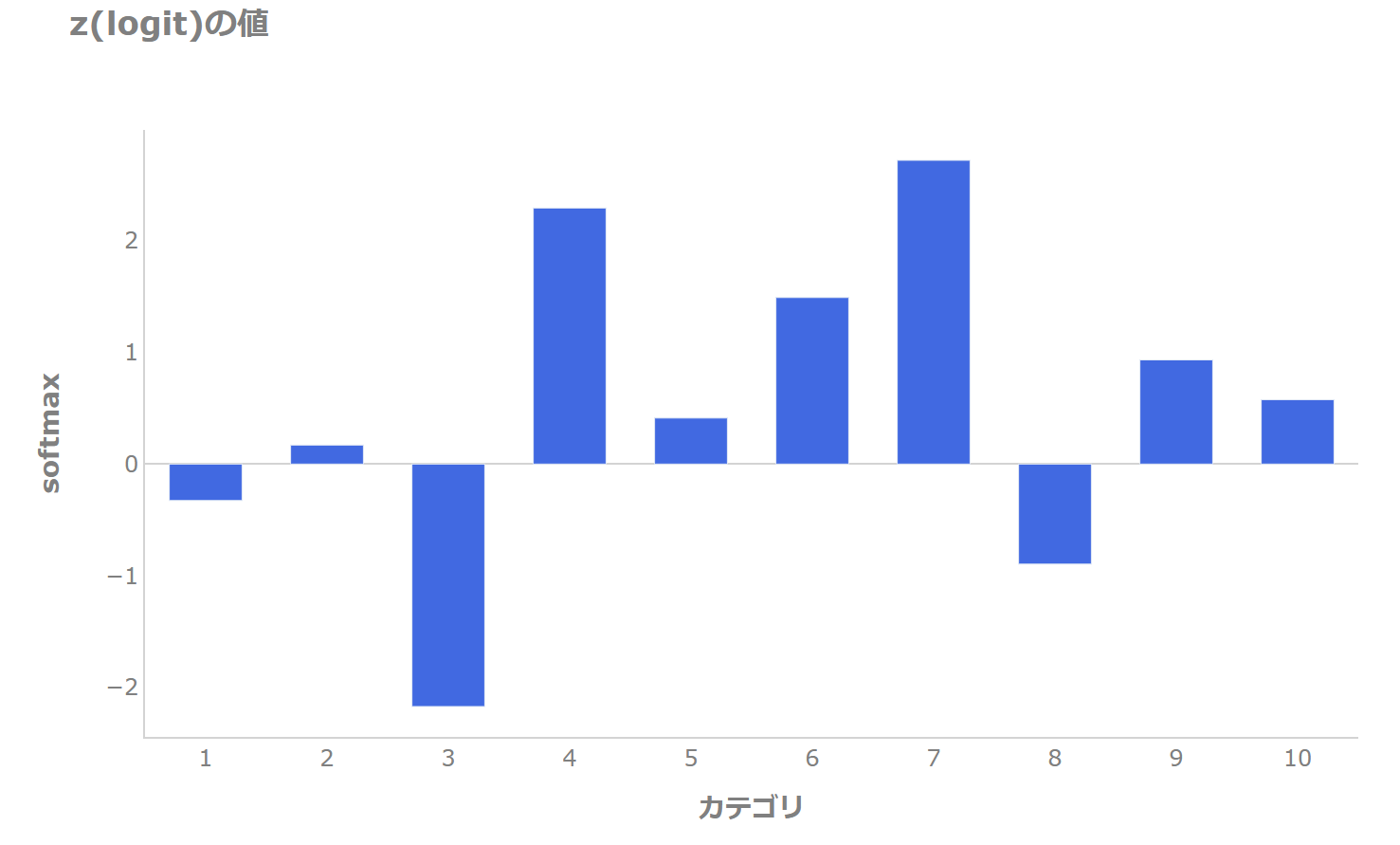
カテゴリ4、7、6が大きめで、3が小さくなっています。

通常のsoftmax関数は以下の関数形になります。

$$\begin{align}
\text{softmax}_i({\bf{z}})=\frac{\exp(z_i)}{\sum_j\exp(z_j)}
\end{align}$$

ですので、softmax関数では以下のような確率を返します。

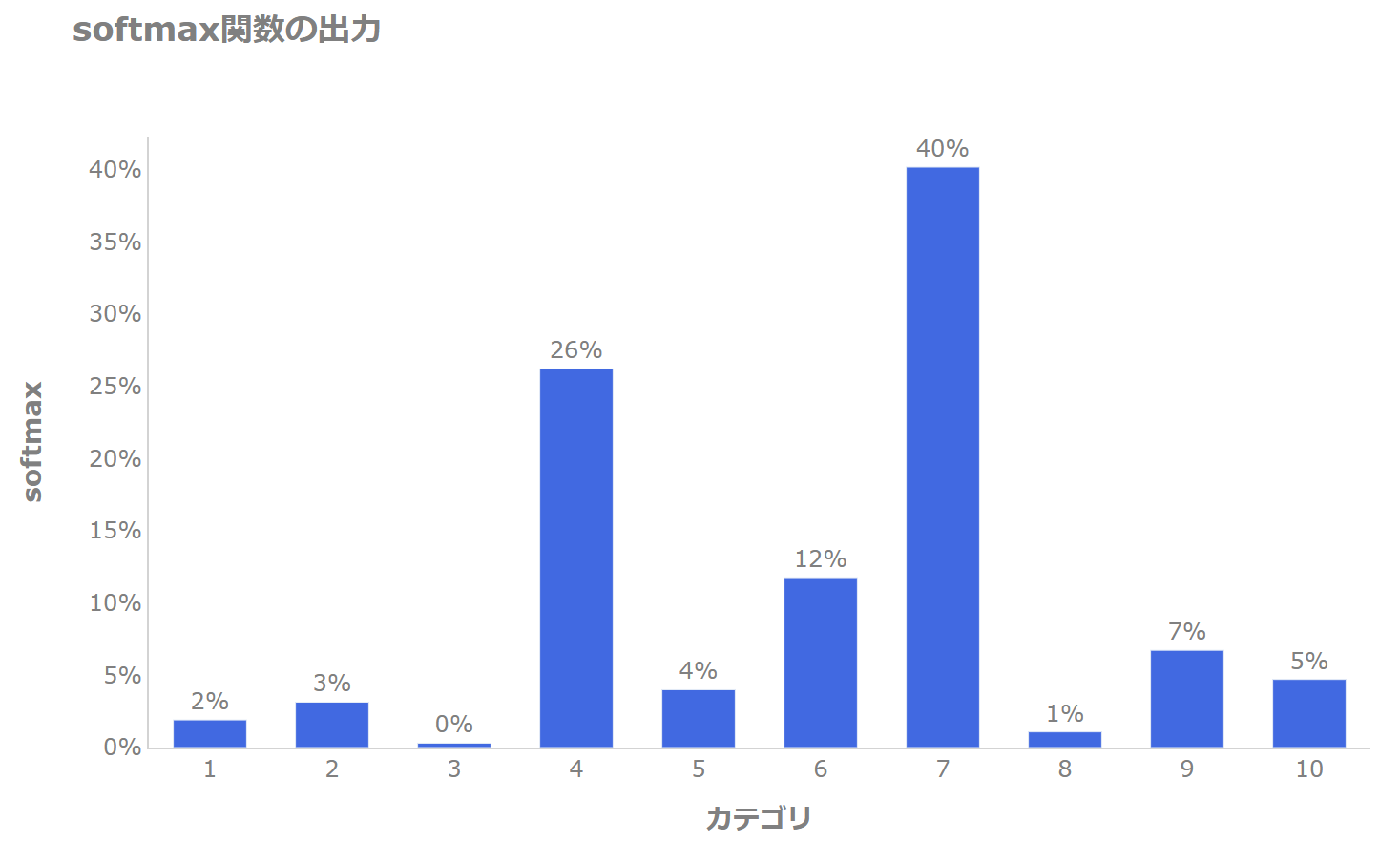
$z$が大きいカテゴリ4とカテゴリ7の確率が大きくなり、それ以外は小さめの確率ですが、すべて非ゼロです(ゼロに近いものはあります)。

Sparsemax関数

では、sparsemax関数ではどうなるかを見てみましょう。

結論としては、上記の$z$の場合、以下のような確率を返します。

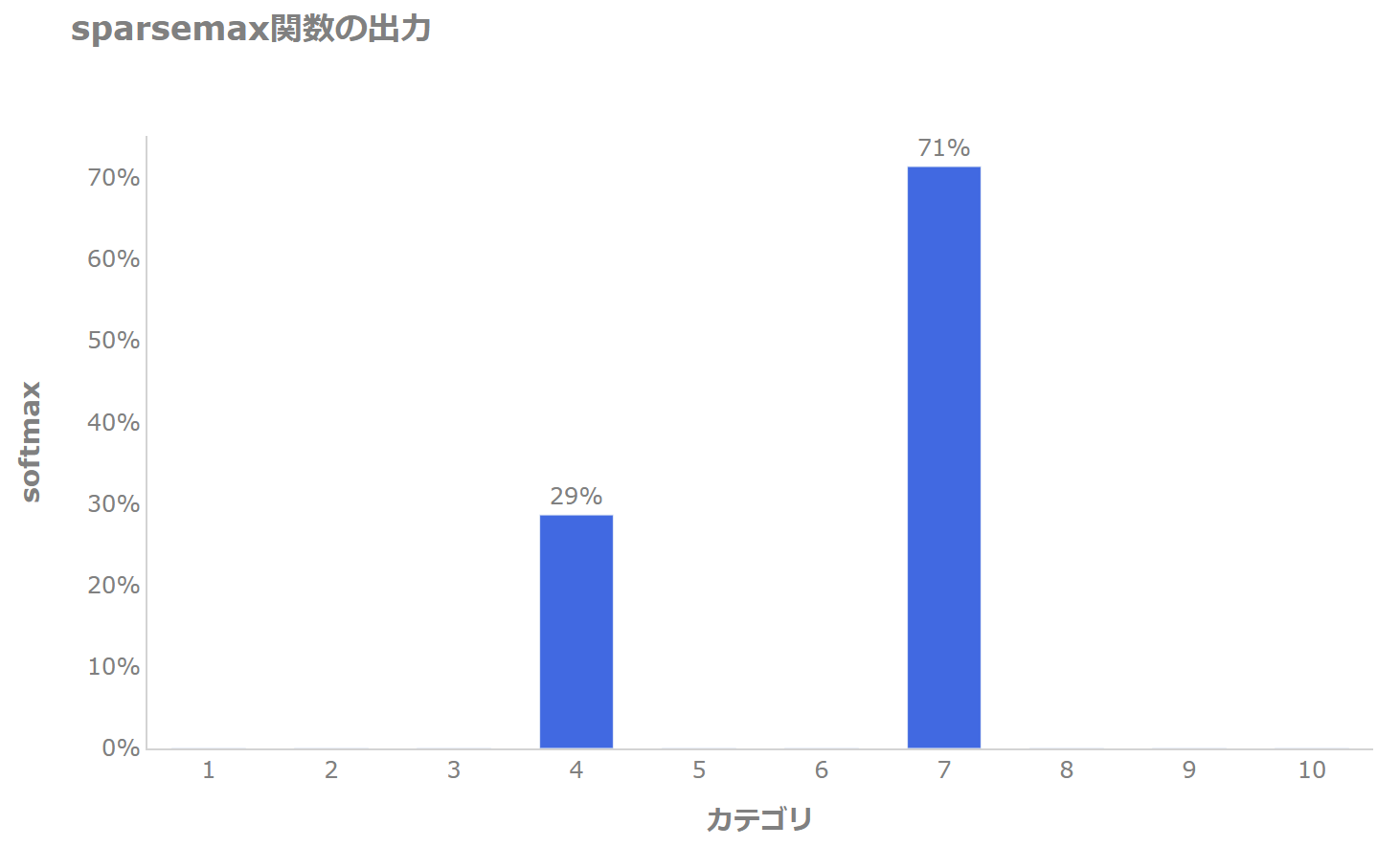
softmax関数で確率の大きかった2点のみが非ゼロで、それ以外はゼロとなっており、スパースなsoftmaxになっているのが確認できます。

では、どのようにしてこれを実現しているかを見てみましょう。

Sparsemax関数のアルゴリズム

まずは、理屈を説明する前に、感覚をつかむためにアルゴリズムを見てみましょう。

インプットは${\bf{z}}=(z_1, \cdots, z_K)$とし、最初にこれを降順で並べ替えます。

並び替えたものを$z_{(1)}\ge \cdots \ge z_{(K)}$とカッコつきの添え字で表現します。

そして、

$$1+kz_{(k)}>\sum_{j\le k}z_{j}$$

を満たすインデックスの中で最大のインデックス$k$を求め、これを$k({\bf{z}})$とします。

その添え字$k({\bf{z}})$を使って$\tau({\bf{z}})$を

$$\tau(z)=\frac{\sum_{j\le k({\bf{z}})}z_{(j)}-1}{k({\bf{z}})}$$

として求めます。

最後に、sparsemaxの確率

$$p_i=\left[z_i-\tau({\bf{z}})\right]_{+}$$

を返します。

つまり、インデックス$k$→$\tau$→$p_i$という形で求めることができます。

Sparsemax関数の理論

さてここまでは、Sparsemax関数がどのようなアウトプットとなるか、どうやって計算するかを簡単に見てきました。

ここからはもう少し理屈について紹介したいと思います。

Sparsemax関数の定義

まず、$\Delta^{K-1}$を以下で定義しておきます。

$$\Delta^{K-1} :=\{ {\bf{p}}\in \mathbb{R}^K | {\bf{1}}^T {\bf{p}} =1, {\bf{p}}\le {\bf{0}} \}$$

カテゴリ数が$K$の場合${\bf{p}}$は$K$次元なので${\bf{p}}\in \mathbb{R}^K$になっています。

そしてその場合、自由度は$K-1$で、残りの一つは$K-1$個の確率の合計を1から引いたものになるので$\Delta^{K-1}$となります。

条件のところは、${\bf{p}}$の合計は1になり、ゼロ以上であるという意味です。

では、この$\Delta^{K-1}$を使ってSparsemax関数を以下で定義します。

$$\text{sparsemax}({\bf{z}}):=\arg \min_{{\bf{p}}\in\Delta^{K-1}} \| {\bf{p}} - {\bf{z}} \|^2$$

ざっくりに言うと、sparsemax関数はlogit ${\bf{z}}$と距離が最も近くなるような確率${\bf{p}}$となります。

ですので、$z_i$がマイナスだと、$p_i$はゼロが与えられる可能性が高くなります。

以上が定義になります。

つまり、上の最適化問題を解いて${\bf{p}}$を求めれば、それがsparsemax関数の出力になります。

解析解

上記の通り、最適化問題を数値的に解けば良いのですが、毎回それをしていては大変です。

ところが、幸いにも解析的に解が求まるようです。

ややこしいですが、解析解は以下になります。

$$\text{sparsemax}_i({\bf{z}})=[z_i-\tau({\bf{z}})]_+$$

ここで、$\tau$は$\sum_j[z_j-\tau({\bf{z}})]_+=1$を満たす関数$\tau: \mathbb{R}^K\rightarrow \mathbb{R}$です。

そして、$\tau$は以下のようにも書けます。

${\bf{z}}$を$z_{(1)}\ge z_{(2)}\ge \cdots\ge z_{(K)}$と降順に並べ替えます。

そして、

$$k({\bf{z}}):=\max\left\{k\in [K]|1+kz_{(k)}>\sum_{j\le k}z_{j}\right\}$$

を定義します。ここで、$[K]=\{1, \cdots, K\}$を表します。

このとき、

$$\tau(z)=\frac{\sum_{j\le k({\bf{z}})}z_{(j)}-1}{k({\bf{z}})}=\frac{\sum_{j\in S({\bf{z}})}-1}{|S({\bf{z}})|}$$

と表されます。

ここで、$S({\bf{z}}):=\{j\in [K]|\text{sparsemax}_j({\bf{z}})>0\}$で、$p_i>0$となるカテゴリの数を表します。

これを計算していたのが上記のアルゴリズムです。

証明

では、なぜそうなるのか、証明を確認しておきましょう。

以下の不等式制約付きの最適化をする問題になります。

$$\begin{align}
\min_{{\bf{p}}\in \mathbb{R}^{K} }\hspace{5pt}& \| {\bf{p}} - {\bf{z}} \|^2\\
\text{s.t. } {\bf{1}}^T {\bf{p}} &=1, \\
{\bf{p}}&\ge {\bf{0}} \\
\end{align}$$

ラグランジアンは

$$\mathcal{L}({\bf{p}}, \mu, \tau) = \frac{1}{2}\|{\bf{p}}-{\bf{z}}\|^2 -\mu^T{\bf{p}} + \tau\left({\bf{1}}^T{\bf{p}}-1\right)$$

になります。

1次の必要条件はKKT条件(Karush-Kuhn-Tucker condition)から導きだすことができ、解は

$$\begin{align}
{\bf{p}} - {\bf{z}} -\mu +\tau {\bf{1}} &={\bf{0}} \tag{1}\\
{\bf{1}}^T{\bf{p}} - 1&={\bf{0}}, \tag{2}\\
{\bf{p}}&\ge {\bf{0}},\tag{3}\\
\mu&\ge {\bf{0}},\tag{4}\\
\mu_ip_i&=0, \forall i \in [K]\tag{5}
\end{align}$$

を満たします(ここの詳細については省略しますが、一番最後に参考書を紹介していますので、参考にしてみてください)。

この解を$*$つきで表します。

$p^*_i>0$と$p^*_i=0$に場合分けをして解いていきます。

**$p^*_i>0$**の場合

まず、$p^*_i>0$の場合を考えます。

(5)式の$\mu_ip_i=0, \forall i \in [K]$という条件から、$p^*_i>0$のとき$\mu^*_i>0$になります。

したがって、(1)式より、

$$p^*_i-z_i+\tau^*=0$$

となるので、

$$p^*_i=z_i-\tau^*\tag{6}$$

が得られます。

$p_i^*>0$より$z_i>\tau^*$が成立しています。

ここで、$p^*_i>0$のインデックスの集合を$S({\bf{z}})$とします。

$$S({\bf{z}})=\{j\in[K]|p_j^*>0\}$$

すると、(2)式$\sum^K_{j=1}p^*_j=1$より、

$$\begin{align}
\sum^K_{j=1}p^*_j &=\sum_{j\in S({\bf{z}})}p_j^*\\
&=\sum_{j\in S({\bf{z}})}(z_j-\tau^*)\\
&=\sum_{j\in S({\bf{z}})}z_j-|S({\bf{z}})|\tau^*=1\\
\end{align}$$

となります。

そこから、

$$\tau^*=\frac{\sum_{j\in S({\bf{z}})}z_j-1}{|S({\bf{z}})|}\tag{7}$$

が得られます。

$\tau^*$は$p_i>0$となる$z_i$の値を使って求めることができます。

以上で、$p_i^*$と$\tau^*$の計算式が求まりました。

あとは、$\tau^*$を計算するために必要なのは、$p^*_j>0$となるインデックスの集合$S({\bf{z}})$です。

**$p^*_i=0$の場合**

では、今までは$p_i^*>0$の場合を考えてきましたが、次に$p_i^*=0$の場合を考えます。

$p_i^*=0$の場合は、(1)式より

$$-z_i-\mu^*_i+\tau^*=0$$

となり、

$$\mu_i^*=\tau^*-z_i\ge 0$$

となります。最後は(4)式$\mu\ge {\bf{0}}$を使っています。

つまり、$p_i^*=0$の場合は、

$$z_i\le \tau^*$$

が成立します。

ここで、

$$\tau^*=\frac{\sum_{j\in S({\bf{z}})}z_j-1}{|S({\bf{z}})|}$$

という関係が得られているので、$p_i^*=0$の場合、

$$z_i\le \frac{\sum_{j\in S({\bf{z}})}z_j-1}{|S({\bf{z}})|}$$

という関係が成立します。

つまり、$p_i>0$の場合は、$z_i>\tau^*$、$p_i=0$の場合は$z_i\le \tau^*$となります。

logit $z_i$が閾値$\tau^*$より小さければ$p^*=0$、大きければ$p>0$ということですね。

図で描くと以下のようになります。

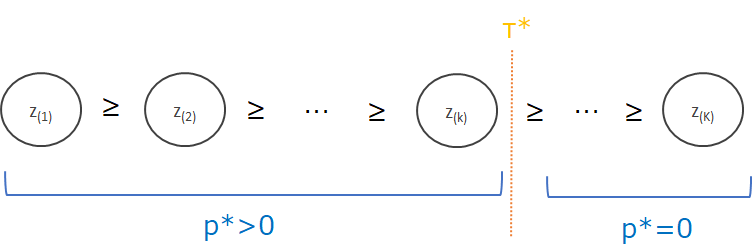
$z_i$を降順に並べ替え、$z_{(k)}\le\frac{\sum_{j\in S({\bf{z}})}z_j-1}{|S({\bf{z}})|}$が成立する$k$については、$p_k^*=0$となります。

逆に上記が成立しない$k$については、$p^*_i=z_i-\tau^*$となります。

さて、$\tau^*$は、

$$\tau^*=\frac{\sum_{j\in S({\bf{z}})}z_j-1}{|S({\bf{z}})|}$$

で表されましたが、そのためには$S({\bf{z}})$、つまり、$p_i^*>0$となるインデックス$i$の数を求める必要があります。

$i\in S({\bf{z}})$の領域では、$z_i>\tau^*$なので、

$$z_i> \frac{\sum_{j\in S({\bf{z}})}z_j-1}{|S({\bf{z}})|}$$

が成立していることになります。

つまり、

$$1+|S({\bf{z}})| z_i> \sum_{j\in S({\bf{z}})}z_j\tag{8}$$

が成立していることになります。

ですので、先ほどと同様に$z_i$を降順$z_{(k)}$で並べ替えた場合、上式を満たす添え字$k$は、

$$k({\bf{z}})=\max\left\{ k\in[K]\left|1+kz_{(k)} >\sum_{j\le k}z_{(j)} \right.\right\}\tag{9}$$

と表されます。$k({\bf{z}})=S({\bf{z}})$です。

図で描くとこちらになります。

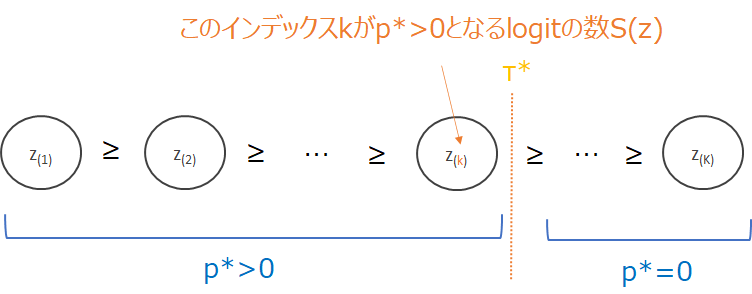
そして、$k({\bf{z}})$より大きな添え字をもつ$z_{(k)}$が$p_k^*\neq 0$となり、(6)式より確率は$p^*_{(k)}=[z_{(k)}-\tau^*]_+$となります。

実装

では、理屈もアルゴリズムもわかりましたので、実装をして確認してみましょう。

まず、$z_i$を降順でソートしましょう。

# sort
z_sorted = np.sort(z, axis=0)[::-1]

(9)式の不等号が成立しているインデックスを求めます。

# 左辺
lhs = 1 + np.arange(1, len(z_sorted)+1) * z_sorted 
# 右辺
rhs = np.cumsum(z_sorted)
# 不等号が成立しているか
larger = lhs > rhs

この場合、不等号が成立している要素の合計が$k({\bf{z}})$になります((8)式)。

# Trueとなっている最大のインデックスを返す
k = larger.sum()

(7)式に従って$\tau^*$を求めましょう。$k({\bf{z}})=S({\bf{z}})$ですので、以下で求まります。

tau = (np.cumsum(z_sorted)[k - 1] - 1) / k

最後に$p^*_i=[z_i-\tau^*]_+$でsparsemax関数による確率を計算します。

p_sparsemax = (z - tau) * (z >= tau)

では、グラフを描いてみましょう。

私はplotlyを使っているので、以下のようなコードで描画します。plotlyについては『Python Plotly入門（①基本的な使い方）』をご参照ください。

text = [f'{y:0.0%}' if y!=0 else '' for y in p_sparsemax]
data = go.Bar(x=np.arange(1, 11),
              y=p_sparsemax,
              marker_color='royalblue',
              width=0.6,
              textposition='outside',
              text=text,
              textfont=dict(color='grey'))
layout = go.Layout(plot_bgcolor='white',
                   title=dict(text='<b>softmax関数の出力',
                              font_color='grey'),
                   xaxis=dict(title='<b>カテゴリ',
                              showline=True,
                              linecolor='lightgrey',
                              linewidth=1,
                              color='grey',
                              dtick=1),
                   yaxis=dict(title='<b>softmax',
                              showline=True,
                              linecolor='lightgrey',
                              linewidth=1,
                              tickformat='%',
                              color='grey'),
                   width=800,
                   height=500)

go.Figure(data, layout)