品詞タグ付け(part-of-speech tagging)を理解する

今回は、自然言語処理で代表的なタスクの一つである“品詞タグ付け(part-of-speech tagging”について解説したいと思います。

以下の本を参考にしています。

1 品詞タグ付け(part-of-speech tagging)とは
2 隠れマルコフモデル(Hidden Markov Model; HMM)
3 品詞列を予測する
4 まとめ

品詞タグ付け(part-of-speech tagging)とは

品詞タグ付けとは、文章中の単語に対して品詞を振ることを指し、系列(単語列)に対してラベルを振っていく“系列ラベリング”の一つです。

英語の翻訳で有名な例では、

Time flies like an arrow.

ということわざの翻訳があります。

これは“光陰矢のごとし”で、直訳すると“時間は矢のように飛んでいく”となります。

これは

Time	flies	like	an	arrow
名詞	動詞	前置詞	冠詞	名詞

という風に品詞を振っています。

しかしながら、昔の翻訳では、これを

Time	flies	like	an	arrow
名詞	名詞	動詞	冠詞	名詞

と読んで、“時間蝿は矢を好む”と訳すこともありました。

意味を考えるとあり得ないのかもしれませんが、機械的に品詞を判断しようとするとこういうことが起こります。

ここでは、“隠れマルコフモデル(Hidden Markov Model)”と呼ばれるシンプルなモデルを使って、品詞タグ付けを行う方法をご紹介したいと思います。

品詞タグ付けなどの系列ラベリングの難しいところは、文章の各単語に対してラベルを振っていくため、可能なラベル列の組み合わせが非常に多いことです。

例えば、一つの文章についてセンチメントを予測する場合の選択肢はセンチメントの数だけで、たいていは5個とかその程度です。

一方で、品詞タグ付けの場合、1つの文章に単語が20個、そしてラベルとなる品詞が10個だとすると、10²⁰個の組み合わせが存在します。

これを効率的に解く方法には“ビタビアルゴリズム”があります。

このビタビアルゴリズムは、固有表現抽出や形態素への分析においても使われていますんで、別の記事でご紹介したいと思います。

隠れマルコフモデル(Hidden Markov Model; HMM)

隠れマルコフモデルとは、観測されない潜在的な状態がある確率で遷移し、遷移した各状態からある確率で観測値が出力されると考えるモデルです。

例えば、裏では“景気の良し悪し”というような目に見えない状態があり、それが一定の確率で遷移しています。

そして、その景気の良し悪しによって、例えば失業率や特定の企業の売上が観測されているというようなものです。

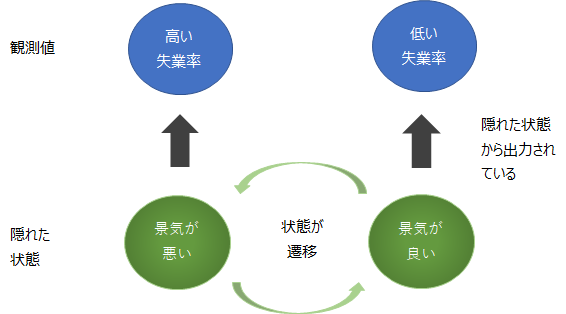
つまり、景気が良い状態のときには、失業率が低い数字が出てきて、景気が悪い状態のときには、失業率が高い数字が出てくる、というようなモデルです。

これを品詞タグ付けに当てはめるとどうなるでしょう。

品詞タグ付けの問題では、隠れた状態が品詞であり、その品詞から単語が出力され観測される、と考えます。

単語列が与えられたときの品詞ラベル列の推定

では、具体的に見ていきましょう。

まず、観測値である単語の系列を${\bf{x}}$、隠れ状態を表すラベルの列を${\bf{y}}$とします。

単語${\bf{x}}$が与えられたときの品詞ラベル列が${\bf{y}}$である確率$P({\bf{y}}|{\bf{x}})$を最も高い品詞ラベルを見つけることを考えると、

$$\begin{align}
\hat{\bf{y}} &= \arg\max_{\bf{y}}P({\bf{y}}|{\bf{x}}) \\
&=\arg\max_{\bf{y}} \frac{P({\bf{x}},{\bf{y}})}{P({\bf{x}})} \\
&=\arg\max_{\bf{y}} \frac{P({\bf{x}}|{\bf{y}})P({\bf{y}})}{P({\bf{x}})} \\
&=\arg\max_{\bf{y}} P({\bf{x}}|{\bf{y}})P({\bf{y}}) \\
\end{align}$$

となります。

1階のマルコフ性を利用した単純化

ここでマルコフ性という仮定を置きます。

ここでは特に、1階のマルコフ性、つまりその時点の状態は一つ前の状態のみに依存するという仮定を置きます。

なお、2つ前までの状態に依存する場合には、2階のマルコフ性と言い、一般化するとN階のマルコフ性と言います。

つまり、$i$番目の状態$y_i$が取る値は直前の$y_{i-1}$が取っている値にのみに依存します。

さらに、$i$番目の単語$x_i$は$y_i$から出力されるので、$x_i$は$y_i$にのみ依存します。

それでは、この仮定を使って$P({\bf{y}}|{\bf{x}})$をシンプルにしていきます。

条件付き確率の計算により、

$$\begin{align}
P({\bf{x}}|{\bf{y}})&=P(x_1, \cdots, x_M| y_1, \cdots, y_M)\\
&=P(x_M| x_1\cdots, x_{M-1}, y_1, \cdots, y_{M})P(x_1, \cdots, x_{M-1}|y_1, \cdots, y_{M})\\
&=\cdots\\
&=\prod_i P(x_i| x_1, \cdots, x_{i-1}, y_1,\cdots,y_{M})\\
&=\prod_i P(x_i| y_{i})
\end{align}$$

と表されます。

ここで、最後の行は、$i$番目の出力単語$x_i$は$i$番目の品詞$y_i$にしか依存しないと仮定していることを使っています。

同様に、

$$\begin{align}
P({\bf{y}}) &= P(y_1,\cdots,y_M)\\
&=\prod_i P(y_i|y_1, \cdots, y_{i-1})\\
&=\prod_i P(y_i|y_{i-1})
\end{align}$$

が得られます。

最後の行がまさに1階のマルコフ性です。

くどくなってしまいましたが、以上より、

$$\begin{align}
\hat{\bf{y}} &= \arg\max_{\bf{y}}P({\bf{y}}|{\bf{x}}) \\
&=\arg\max_{\bf{y}} \prod_i P(x_i|y_i) P(y_i|y_{i-1}) \\
\end{align}$$

が導出されます。

アンダーフローについての補足

$\prod_i P(x_i|y_i) P(y_i|y_{i-1})$は、1より小さい確率の積になります。場合によっては、要素がきわめて小さな数値を取ることもあるので、それを掛け合わせるとアンダーフローが起こってしまいます。

そこで実際は、対数を取ったものを最大化することで、

$$\begin{align}
\hat{\bf{y}} &= \arg\max_{\bf{y}}P({\bf{y}}|{\bf{x}}) \\
&= \arg\max_{\bf{y}} \log P({\bf{y}}|{\bf{x}}) \\
&=\arg\max_{\bf{y}} \sum_i \left( \log P(x_i|y_i) + \log P(y_i|y_{i-1})\right) \\
\end{align}$$

アンダーフローを避けることができます。

パラメータの推定

実際にこの確率を求めるには、パラメータ$P(x_i| y_i)$と$P(y_i|y_{i-1})$がわかっている必要があります。

$P(x_i| y_i)$は、$i$番目の品詞が$y_i$であった場合の単語が$x_i$である確率、$P(y_i|y_{i-1})$は前の品詞が$y_{i-1}$であった場合の次の品詞が$y_i$となる確率です。

ようするに、

“単語列が与えられて、それに対応する品詞列を求めるには、一番手前から順番に、その単語と直前の品詞を見て、それに対応しそうな品詞を予測していく”ことになります。

何となく直感的ではないでしょうか？

では、$P(x| y)$と$P(y| y')$($y'$は$y$の直前の品詞を表す)は、最尤推定を用いて

$$\begin{align}
P(x| y)&=\frac{単語がxで品詞がyである回数}{品詞がyである回数}\\
P(y| y')&=\frac{直前の品詞がy'で次の品詞がyであるの回数}{直前の品詞がy'である回数}
\end{align}$$

で計算することができます。

すべてのデータを使って、それぞれ$P(x| y)$と$P(y| y')$を計算います。
より詳細について知りたい方は、『言語処理のための機械学習入門 (自然言語処理シリーズ)』をご参照ください。

これにより、単語列${\bf{x}}$が与えられた場合のラベル列が${\bf{y}}$となる確率を求めることができました。

品詞列を予測する

さて、ここまでで、単語列${\bf{x}}$とラベル列${\bf{y}}$が与えられた場合の、それが起こる確率が求めることができるようになりました。

解くべきタスクは、単語列${\bf{x}}$が与えられて、そのラベル列${\bf{y}}$を予測することです。

ラベル列${\bf{y}}$を求める方法は、すべての組み合わせの中で最も確率の高いラベル列を選びます。

つまり、

$$\begin{align}
\hat{\bf{y}} &=\arg \max_{\bf{y}} P({\bf{y}}| {\bf{x}}) \\
&=\arg\max_{\bf{y}} \sum_i \left( \log P(x_i|y_i) + \log P(y_i|y_{i-1})\right)
\end{align}$$

という問題を解きます。

しかしながら、すべての組み合わせに対して$P({\bf{y}}| {\bf{x}})$を求めて、一番確率の高いラベル列${\bf{y}}$を求めるというのは、組み合わせ数が膨大になりすぎて、現実的ではりません。

そこで、“ビタビアルゴリズム(Viterbi Algorithm)”を使うことで効率的に求めることができます。

ビタビアルゴリズムについては、以下の記事で解説していますので、続きが気になる方はこちらをご覧ください。

: 品詞タグ付け(part-of-speech tagging)を理解する - ビタビアルゴリズム
『品詞タグ付け(part-of-speech tagging)を理解する』では、隠れマルコフモデルを使って、単語列xが与えられたときに品詞ラベル列がyとなる確率の求め方を解説しました。まだ、このまま ...