品詞タグ付け(part-of-speech tagging)を理解する - ビタビアルゴリズム

『品詞タグ付け(part-of-speech tagging)を理解する』では、隠れマルコフモデルを使って、単語列xが与えられたときに品詞ラベル列がyとなる確率の求め方を解説しました。

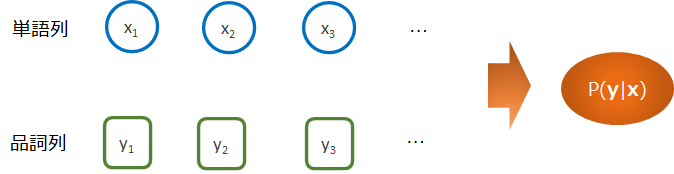
まだ、このままでは各単語列と品詞ラベル列をインプットとして同時分布が求まるだけであり、単語列に対して正しい品詞ラベル列を振ろうと思うと、すべての品詞ラベル列の並び方を試して一番$P({\bf{y}}, {\bf{x}})$が大きくなるような品詞ラベル列${\bf{y}}$を見つけなければなりません。

$P({\bf{y}}|{\bf{x}})$を最大にするようなラベル列${\bf{y}}$を知りたい！
➡ それを効率的に求めるのがビタビアルゴリズム

すべての並び方は、単語が20個、ラベルが10個ある場合で、10²⁰通りもあるので、手あたり次第計算することは現実的ではありません。

そこで、動的計画法の一種である"ビタビアルゴリズム(Viterbi Algorithm)"を利用します。

ビタビアルゴリズムは、形態素解析における形態素への分割や、固有表現抽出などにも使われている方法です。

では、詳細を解説していきたいと思います。

今回は、こちらの本を参考にしています。

1 ビタビアルゴリズム
2 ビタビアルゴリズムの手順
- 2.1 前向き
- 2.2 後ろ向き
3 ビタビアルゴリズムの具体例
4 まとめ

ビタビアルゴリズム

まず、隠れマルコフモデルでは、$i$番目の品詞ラベルは$i-1$番目の品詞ラベルにしか依存しないという1階のマルコフ性の仮定をおいていました。

ですので、多数の品詞ラベル列の候補の中から、最適な品詞ラベル列を求める問題は以下のように表されました。

$$\begin{align}
\hat{\bf{y}} &= \arg\max_y P({\bf{y}}|{\bf{x}})\\
&=\arg\max_{\bf{y}} \prod_i P(x_i|y_i) P(y_i|y_{i-1})\\
&=\arg\max_{\bf{y}} \sum_i \left( \log P(x_i|y_i) + \log P(y_i|y_{i-1})\right)
\end{align}$$

そして、$P(x_i|y_i)$、$P(y_i|y_{i-1})$は、

$$\begin{align}
P(x| y)&=\frac{単語がxで品詞がyである回数}{品詞がyである回数}\\
P(y| y')&=\frac{直前の品詞がy'で次の品詞がyであるの回数}{直前の品詞がy'である回数}
\end{align}$$

で求めればよいことを説明しました。

$log P(y_i|y_{i-1})$を見ると、一つ前の品詞だけに依存するということです。

それを利用して、前から順番に、確率(の対数)が最大になるような品詞を選んでいくことで、最終的に品詞列として確率を最大にするように求めていきます。

したがって、すべての経路を考えるのではなく、ある時点までの最適な経路だけを保存しておき、次の時点の品詞ラベルはどれが最適か？を求めていくのがビタビアルゴリズムです。

ビタビアルゴリズムの手順

ここではビタビアルゴリズムの手順を簡単に説明します。

とは言っても、アルゴリズムだけでは結構じっくり考えないとわからないので、ざっくりここを見ていただいたあとに、続きの具体例を見ていただければ理解しやすいと思います。

ビタビアルゴリズムは前向きに最適な経路とそのスコアを計算して保存していき、最後に後ろ向きに最適な経路を抽出するという順番になっています。

それでは、前向きと後ろ向きをそれぞれ見ていきましょう。

前向き

まず、変数を定義しておきます(長い変数名で恐縮ですが、こちらの方がわかりやすいかと思いました…)。

$\widehat{path\_score}_{j, y_j}$
$j$番目の単語の品詞ラベルを$y_j$とした場合の、それまでの経路全体の最大スコア。
$\widehat{path}_{j, y_j}$
$j$番目の単語の品詞ラベルを$y_j$とした場合の、それまでの経路全体のスコアが最大となる一つ前のラベル。
つまり、$\widehat{path\_score}_{j, y_j}$を取る場合の一つ前のラベル。
$score_{j, y_{j-1}\rightarrow y_j}$
$=\log P(x_i|y_i) + \log P(y_i|y_{i-1})$

例えば、$x_3$の品詞ラベルを$L_1$とした場合の、$\widehat{path\_score}_{j, y_j}$はそのときの最適経路のスコアで、$\widehat{path}_{j, y_j}$がその一つ前、つまり$x_2$の品詞ラベルです。

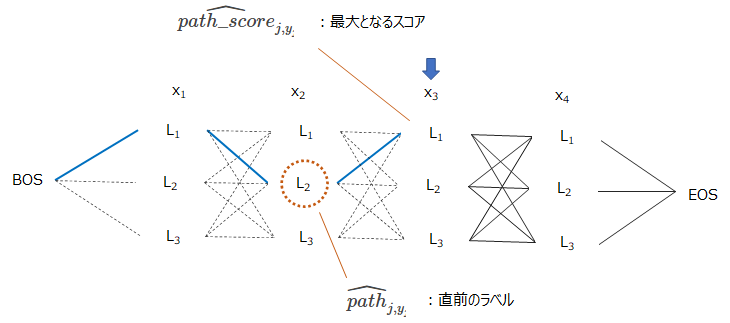
そして、文章中に単語が$J$個あるとして、文頭にBOS($x_0$)、文末にEOS($x_{J+1}$)というダミーのノードを作成し、BOSから順番に以下のアルゴリズムで計算していきます。

前向き

for $j = 1$ to $J+1$
　for all $y_j$,
　　$\widehat{path\_score}_{j, y_j}=\max_{y_{j-1}} \left[\widehat{path\_score}_{j-1, y_{j-1}} +score_{j, y_{j-1}\rightarrow y_j} \right]$
　　$\widehat{path}_{j, y_j}=\arg \max_{y_{j-1}} \left[\widehat{path\_score}_{j-1, y_{j-1}} +score_{j, y_{j-1}\rightarrow y_j} \right]$
　end for
end for

ビタビアルゴリズムは、一つ前($j-1$)の単語までの最適な品詞の経路がわかっており、その時点($j$)の単語の取り得るラベルごとに、(a)最適な経路と(b)最適な経路のスコアを保存していきます。

1行目は、各単語について先頭から順番に進めていきます。

2行目は、各時点において、$y_j$の取るラベルすべてについて最大となるスコアとその経路を求めていきます。

では、続きの真ん中の2行を少し詳しく見ていきましょう。

そのうちの上の行はこのようになっています。

$\widehat{path\_score}_{j, y_j}=\max_{y_{j-1}} \left[\widehat{path\_score}_{j-1, y_{j-1}} +score_{j, y_{j-1}\rightarrow y_j}\right]$

$\max$を除いてみると、1項目の$\widehat{path\_score}_{j-1, y_{j-1}}$は、一つ前の単語のラベルが$y_{j-1}$である場合のそこまでの最適な経路のスコアで、それに2項目の$x_{j-1}$のラベルが$y_{j-1}$で$x_j$のラベルが$y_j$である場合のスコア(確率の対数)$score_{j, y_{j-1}. y_j}$を足しています。

ですので、maxにより複数の経路$y_{j-1}$を通るスコアのうち最大のスコアを取ってきています。

つまり、$j$番目の単語の品詞が$y_j$である場合の最適な経路のスコア$\widehat{path\_score}_{j, y_j}$を計算し、保存しています。

その次の行

$\widehat{path}_{j, y_j}=\arg \max_{y_{j-1}} \left[\widehat{path\_score}_{j-1, y_{j-1}} +score_{j, y_{j-1}\rightarrow y_j} \right]$

はそのときの経路自体を保存するもので、最大となるスコアを取る経路の$j-1$番目のラベルを保存しています。

これは次の後ろ向きのアルゴリズムで使用されます。

後ろ向き

後ろ向きは、前向きで保存した$j$番目で品詞$y_j$を取る場合の最適な一つ前のラベルを使って、一番最後から順番に最適なラベルを選んでいきます。

$\widehat{y}_J = \arg\max_{y} \widehat{path\_score}_{J+1, EOS}$
for $j=J$ to 1
　　$\widehat{y}_j = \widehat{path}_{j, \widehat{y_j}}$
end for

1行目で、最後のEOSの場合の、最適な一つ前の品詞、つまり一番最後の品詞を選んでいきます。

そして、それをもとに順番に確定している一つ前の最適な品詞を抽出しています。

ビタビアルゴリズムの具体例

アルゴリズムだけでは、なかなか理解しづらい部分もあると思いますので、具体例で解説していきたいと思います。

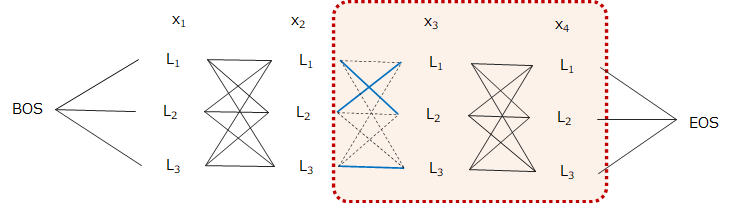
上図のように4つの単語から成る文章に対し、3種類の品詞ラベルから付与する場合を考えます。

4単語の文章に3つのラベルなので候補となるラベル列は81パターンです。

そして、BOSとEOSはそれぞれ文頭と文末を表すダミーです。

前向き

では、4番目の単語$x_4$の赤枠部分のみを考えましょう。

まず、一つ前の単語$x_3$の候補となる品詞ラベル$L_1$、$L_2$、$L_3$に対し、それまで、つまり$x_3$までの最適な経路がわかっていると仮定します。

そして、$x_3$の品詞ラベルが$y_{3}$で、$x_4$の品詞ラベルが$L_1$、$L_2$、$L_3$となる場合のスコアをそれぞれ$score_{4, y_{3}\rightarrow L_1}$、$score_{4, y_{3}\rightarrow L_2}$、$score_{4, y_{3}\rightarrow L_3}$と表し、その直前($x_3$)の最適なラベルを$\widehat{path}_{4, L_1}$、$\widehat{path}_{4, L_2}$、$\widehat{path}_{4, L_3}$と表します($x_4$がどのラベルを取るかによって、$x_3$での最適な品詞ラベルが違ってきます)。

そして、各$y_4=L_1,L_2,L_3$に対して$$\widehat{path\_score}_{3, y_{3}} +score_{4, y_{3}\rightarrow y_4}$$を最大化するような$y_3$を探します。

$x_4$においてスコアが最大となる経路を探す

では、$x_4$の品詞ラベルが$L_1$となる場合を考えます。

一つ前の$x_3$の品詞ラベルは$L_1$、$L_2$、$L_3$とありますが、それぞれ見ていきます。

例えば$x_3$の品詞を$L_1$とした場合(以下の図の赤い線)を考えてみましょう。

以下の図の青い線は、$x_3$が$L_1$であった場合のスコアが最大になる経路になります。

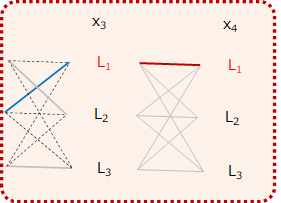
そして、この場合の経路のスコアは、直前までの最適な経路のスコアに、そこからその時点(この場合$x_4$)のスコアを足せばよいので、

$$path\_score_{4, L_1\rightarrow L_1}=\widehat{path\_score}_{3, L_1} + score_{4, L_1\rightarrow L_1}$$

と表されます。

同様に、$x_3$の品詞が$L_2$だった場合、

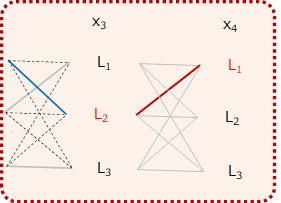
$$path\_score_{4, L_2\rightarrow L_1}=\widehat{path\_score}_{3, L_2} + score_{4, L_2\rightarrow L_1}$$

と表すことができます。

また、$x_3$の品詞が$L_3$だった場合についても、

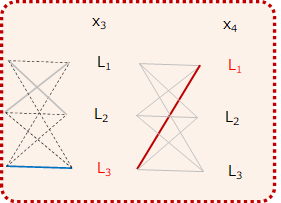
$$path\_score_{4, L_3\rightarrow L_1}=\widehat{path\_score}_{3, L_3} + score_{4, L_3\rightarrow L_1}$$

となります。

そして、この3つのうちでスコアが最大となるものが、$x_4$の品詞が$L_1$となる場合の最適な経路になります。

$$\widehat{path\_score}_{4, y_3\rightarrow L_1}$$

が求まります。$y_3$は$L_1$かもしれませんし、$L_2$もしくは$L_3$かもしれません。

これを同じように、$x_4$のラベルが$L_2$となる場合についても求めることで、

$$\widehat{path\_score}_{4, y_3\rightarrow L_2}$$

$$\widehat{path\_score}_{4, y_3\rightarrow L_3}$$

が求まります。

そして、その各ラベルを取る場合の最大となるスコアと、その経路である一つ前の単語の品詞を

$$\widehat{path}_{4, L_1}, \widehat{path}_{4, L_2}, \widehat{path}_{4, L_3}$$

に保存しておきます。

最後にスコアが最大となる経路を探す

最後のステップを見てみましょう。

最後の部分は以下のようになります。

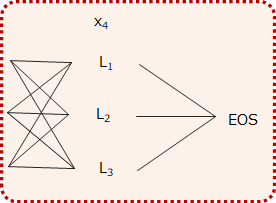
最後はEOSしか取らないので、$x_4$のラベルが$L_1$、$L_2$、$L_3$となる場合それぞれについて、その次にEOSとなる場合のスコアを計算します。

$$\begin{align}
path\_score_{5, L_1\rightarrow EOS}&=\widehat{path\_score}_{4, L_1} + score_{5, L_1\rightarrow EOS}\\
path\_score_{5, L_2\rightarrow EOS}&=\widehat{path\_score}_{4, L_2} + score_{5, L_2\rightarrow EOS}\\
path\_score_{5, L_3\rightarrow EOS}&=\widehat{path\_score}_{4, L_3} + score_{5, L_3\rightarrow EOS}
\end{align}$$

そしてこのうちのスコアが最大のとなる経路が、最終的に系列のスコアを最大化する経路になります。