【PyTorch】VAE(Variational Auto-Encoder)を実装する

さて、以前こちらの記事ではVAE(Variational Auto-Encoder)の解説およびTensorflowを使った実装をしました。

【Python (Tensorflow) による実装付き】Variational Auto-Encoder (VAE) を理解する

今回は、2014年に提案された画像生成モデル “Variational Auto-Encoder (VAE) ” について解説していきたいと思います。 仕組みの詳細まで踏み込んでいるため、計算などが複 ...

TensorflowではなくPyTorchを使っている人も多いと思いますので、今回はPyTorchを使って実装したいと思います(私もPyTorchを使うことが多くなってきましたので)。

VAEの損失関数の導出などといった詳細は解説しませんので、ご興味がある方は上記の記事をご参照いただければと思います。

VAEの概要

VAEとは

VAEは2014年に以下の論文で発表された「画像を生成する生成モデル」です。

『Auto-Encoding Variational Bayes』

オート・エンコーダという名前がついているのは、以下の図のようにインプットである画像\({\bf{x}}\)を\({\bf{z}}\)にエンコードし、それをデコーダで\({\hat{x}}\)に復元するというオートエンコーダのような学習を行うからです。

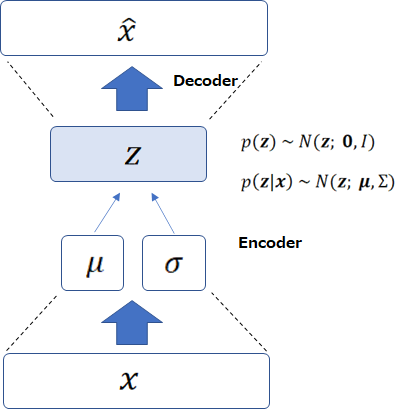
では、通常のオートエンコーダとどう違うのか？というと、違うところは潜在変数\({\bf{z}}\)を導入する点です。

VAEでは\({\bf{z}}\)という潜在変数があって、そこから観測される画像\({\bf{x}}\)が生成されている考えるモデルであり、そこにオートエンコーダを適用したものです。

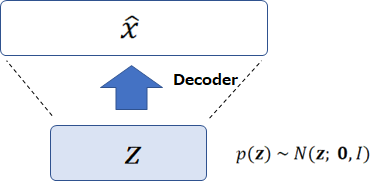
そして、オート・エンコーダはディープラーニングをうまく学習するための事前学習として使われますが、VAEでは以下の図のように、\({\bf{z}}\)を標準正規分布から生成し、学習済みのデコーダで画像を生成するために使います。

VAEの仮定

VAEでは潜在変数\({\bf{z}}\)の(事前)分布に標準正規分布を仮定しています。

つまり、標準正規分布にしたがう見えない\({\bf{z}}\)があって、そこから皆さんが目にするような画像が生成されていると考えます。

したがって、標準正規分布に従う潜在変数をサンプルすこることができ、その潜在変数を使って画像を生成することが可能になっています。

また、潜在変数の事後分布\(p({\bf{z}}|{\bf{x}})\)にも正規分布を仮定しています。

VAEの学習方法

エンコーダでは直接\({\bf{z}}\)を求めるのではなく、\({\bf{x}}\)が観測された際の\({\bf{z}}\)の分布(事後分布)の平均\(\mu\)、分散\(\sigma^2\)をニューラルネットワークで計算します。

つまり、\({\bf{x}}\)が与えられて、そこから\(p({\bf{z}}|{\bf{x}})\)の平均・分散を計算するということです。

しかしながら、潜在変数を用いた生成モデルでは、簡単に周辺尤度\(p_\theta({\bf{x}})\)を計算することができません。

そこで変分推論というベイズ学習の手法を使って、周辺尤度ではなく以下で表される下界(ELBO(Evidence Lower Bound)やVLB(Variational Lower Bound)と呼ばれます)を最大化します。

(詳細については、『【Tensorflowによる実装付き】Variuational Auto-Encoder(VAE)を理解する』をご参照ください。)

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta)&= \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] - D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

この1項目の期待値を以下のように近似して、モンテカルロ法で計算します。

$$\begin{align}
\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right]&\simeq \frac{1}{L} \sum_{l=1}^L \log p_\theta({\bf{x}}|{\bf{z}}^{(l)}), \\
{\bf{z}}^{(l)}&=\mu(\phi) + \sigma(\phi) \odot {\bf{\epsilon^{(l)}}}, \hspace{10pt} \epsilon^{(l)}～N(\epsilon; 0, I)
\end{align}$$

\(L\)は1として、1つのサンプルで計算することが一般的です。

2項目の\(D_{KL}\)はカルバック・ライブラー・ダイバージェンスですが、\(p\)も\(q\)も正規分布なので簡単な形に変形することができ、以下で求まります。

$$D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)=-D\frac{1}{2}\sum_{j=1}^{D}\left(1+\log \sigma^2_j - \mu_j^2 -\sigma^2\right)$$

これで2つの項が求まり、これを損失関数とします。

このように学習することでVAEという画像生成モデルを学習することができます。

式がややこしいため抵抗があるかもしれませんが、まずは実装を見ていただければ、非常にシンプルだということをわかっていただけると思います。

PyTorchでVAEを実装する

では、さっそくVAEを実装しましょう。

まずは必要なモジュールのインポートをします。

# PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F

# PyTorch画像用
import torchvision
import torchvision.transforms as transforms

# 画像表示用
import matplotlib.pyplot as plt

続いてデータセットを取得します。

今回はMNISTの手書きの数字データを使用します。

今ではあまり面白味のないデータですが、もう少し面白い画像だとVAEの場合ぼやけてしまうのでうまくいきませんでした。

そういった画像は今後VQ-VAEなどで試したいと思っています。

ということで、MNISTデータをロードし、バッチサイズを128としてDataLoaderを作成しましょう。

batch_size = 128

# データセットの取得
train_dataset = torchvision.datasets.MNIST(
    root='./data',
    train=True,
    transform=transforms.ToTensor(),
    download=True,
)
# DataLoaderの作成
train_loader = torch.utils.data.DataLoader(
    dataset=train_dataset,
    batch_size=batch_size,
    shuffle=True,
    num_workers=0
)

次は、モデルの部分です。

エンコーダ

観測画像から潜在変数を生成するエンコーダの実装です。

まず、全結合層で処理し、そのあとに正規分布の平均\(\mu\)と分散\(\sigma^2\)(実際は負の値を取ってもいいように\(\log \sigma^2\))をそれぞれ全結合で計算します。

class Encoder(nn.Module):
  def __init__(self, input_dim, hidden_dim, latent_dim):
    super(Encoder, self).__init__()
    self.fc = nn.Linear(input_dim, hidden_dim)
    self.fc_mu = nn.Linear(hidden_dim, latent_dim)
    self.fc_var = nn.Linear(hidden_dim, latent_dim)
 
  def forward(self, x):
    # ニューラルネットワークで事後分布の平均・分散を計算する
    h = torch.relu(self.fc(x))
    mu = self.fc_mu(h) # μ
    log_var = self.fc_var(h) # log σ^2

    # 潜在変数を求める
    ## 標準正規乱数を振る
    eps = torch.randn_like(torch.exp(log_var))
    ## 潜在変数の計算 μ + σ・ε
    z = mu + torch.exp(log_var / 2) * eps
    return mu, log_var, z

さらに求まった平均・分散を使って、各サンプルに一つの正規乱数を振って潜在変数\({\bf{z}}\)を求めています。

デコーダ

デコーダは潜在変数から画像を復元します。

ここでは2つの全結合層を使います。

最後の全結合層の活性化関数はシグモイド関数として、0~1の値を返します。

class Decoder(nn.Module):
  def __init__(self, input_dim, hidden_dim, latent_dim):
    super(Decoder, self).__init__()
    self.fc = nn.Linear(latent_dim, hidden_dim)
    self.fc_output = nn.Linear(hidden_dim, input_dim)
    
  def forward(self, z):
      h = torch.relu(self.fc(z))
      output = torch.sigmoid(self.fc_output(h))
      return output

VAE全体

作成したエンコーダとデコーダをつなげて、VAEのモデルを作成します。

class VAE(nn.Module):
  def __init__(self, input_dim, hidden_dim, latent_dim):
    super(VAE, self).__init__()
    self.encoder = Encoder(input_dim, hidden_dim, latent_dim)
    self.decoder = Decoder(input_dim, hidden_dim, latent_dim)
   
  def forward(self, x):
    mu, log_var, z = self.encoder(x) # エンコード
    x_decoded = self.decoder(z) # デコード
    return x_decoded, mu, log_var, z 

学習コード

では、モデルが出来上がったので学習のためのコードを書いていきます。

損失関数

下界は以下で表されますので、1項目を再構築項、2項目をKLダイバージェンス項として、それぞれ計算します。

$$\begin{align}
\mathcal{L}({\bf{x}}, \phi, \theta)&= \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] - D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

下界の最大化をしたいで、損失関数としては負の下界になります。

$$\begin{align}
\text{Loss function}&= -\mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] + D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)
\end{align}$$

負の再構築項はクロスエントロピー誤差として計算することができます。

そして、2項目のKLダイバージェンス項は、以下で計算できます。

$$D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)=-\frac{1}{2}\sum_{j=1}^{D}\left(1+\log \sigma^2_j - \mu_j^2 -\sigma^2\right)$$

def loss_function(label, predict, mu, log_var):
  reconstruction_loss = F.binary_cross_entropy(predict, label, reduction='sum')
  kl_loss = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
  vae_loss = reconstruction_loss + kl_loss
  return vae_loss, reconstruction_loss, kl_loss

学習

ハイパーパラメータを設定します。

そして、モデルを生成して、オプティマイザをAdamにします。

image_size = 28 * 28
h_dim = 32
z_dim = 16
num_epochs = 10
learning_rate = 1e-3

model = VAE(image_size, h_dim, z_dim).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

では、学習しましょう。

予測⇒損失の計算⇒パラメータの更新⇒損失の表示という順に進めます。

losses = []
model.train()
for epoch in range(num_epochs):
  train_loss = 0
  for i, (x, labels) in enumerate(train_loader):
    # 予測
    x = x.to(device).view(-1, image_size).to(torch.float32)
    x_recon, mu, log_var, z = model(x)
    # 損失関数の計算
    loss, recon_loss, kl_loss = loss_function(x, x_recon, mu, log_var)
    
    # パラメータの更新
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    # 損失の表示
    if (i+1) % 10 == 0:
      print(f'Epoch: {epoch+1}, loss: {loss: 0.4f}, reconstruct loss: {recon_loss: 0.4f}, KL loss: {kl_loss: 0.4f}')
    losses.append(loss)

画像の生成

以下のコードで、正規分布に従う潜在変数\({\bf{z}}\)を生成し、そこからモデルのデコーダで画像を生成します。

model.eval()

with torch.no_grad():
  z = torch.randn(25, z_dim).to(device)
  out = model.decoder(z)
out = out.view(-1, 28, 28)
out = out.cpu().detach().numpy()

では、表示してみましょう。

fig, ax = plt.subplots(nrows=5, ncols=5, figsize=(10, 10))
plt.gray()
for i in range(25):
  idx = divmod(i, 5)
  ax[idx].imshow(out[i])
  ax[idx].axis('off');   
fig.show()

こんな感じの数字が生成されています。

ハイパーパラメータをもう少しいじれば、多少良くなるかもしれませんが、VAEは結構ぼやけてしまいます。

おいおいVAEがぼやけてしまうという欠点に対応したVQ-VAEについてもPyTorchで実装したいと思っています。

まとめ

今回はVAEをPyTorchで実装しました。

ここでは、EncoderクラスとDecoderクラスを作成し、VAEクラスから呼び出しましたが、VAEクラスにエンコードメソッド、デコードメソッドをそのまま書いてやると、もっとシンプルにすることができますので、皆さんも試していただければと思います。

PyTorchを体系的に学びたいという方は以下の書籍がオススメです。

PyTorchを使いながら比較的新しいディープラーニング技術を幅広に学びたいという方はこちらの書籍がオススメです。

では、今度はConditional VAE、VQ-VAEをPyTorchで実装したいと思います。

では！