今回は、VQ-VAE(Vector Quantised-Variational AutoEncoder)を解説したいと思います。
VQ-VAEもVAE(Variational AutoEncoder)と同じで潜在変数を使った画像などの生成モデルです。
通常のVAEと違うところは、VAEでは潜在変数\(z\)が連続的なベクトルを取りましたが、VQ-VAEでは潜在変数が離散的なベクトルを取る点です。
画像や自然言語は本来離散的なもので、例えば「犬」から「猫」へ少しずつ変化していくものでありません。
ですので、潜在変数を離散的にすることは自然であると言えます。
では、以下の論文をもとに解説していきたいと思います。
『Neural Discrete Representation Learning』
最後にTensorflowで実装していますので、そちらも参考にしていただければと思います。
PyTorchの実装はこちらです(モデルの詳しい解説はしていません)。
VAEについては、こちらの記事をご参照ください。
VQ-VAE
VAEは、潜在変数の事後分布\(q(z|x)\)、潜在変数の事前分布\(p(z)\)、\(p(x|z)\)を持つデコーダのパラメータを推定しましたが、潜在変数の事前分布、事後分布に正規分布を仮定していました。
VQ-VAEでは、潜在変数の事前分布、事後分布をカテゴリカル分布とするという特徴があります。
詳細は後程説明しますが、以下の左側の図のように、エンコーダで\(z_e\)を求め、そこから離散的なK種類の埋め込み表現(Embeddings)にマッピングします。
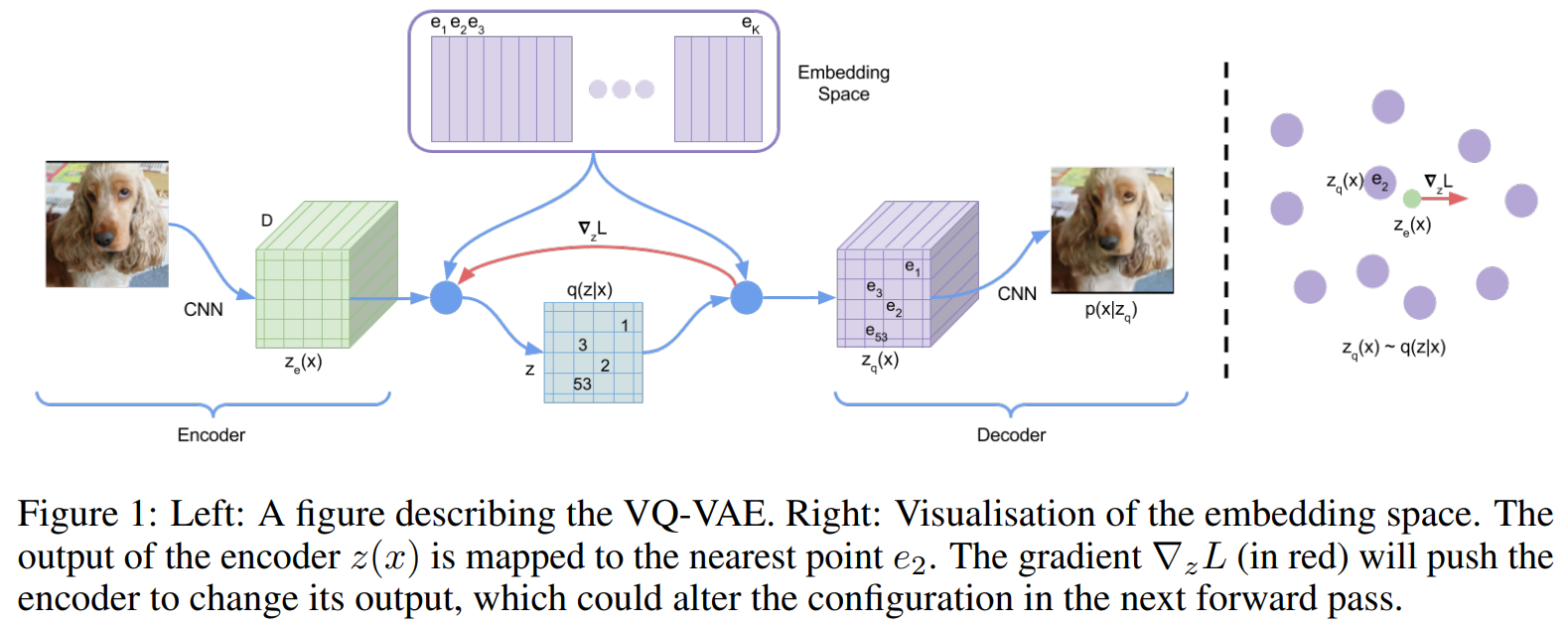
つまり、32x32の画像であれば、各ピクセルについて、ここはK種類のうちの3番目の埋め込み表現、ここは15番目の埋め込み表現といった形で、1~Kまでのインデックスを設定します。
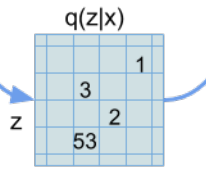
この埋め込み表現を使って画像の以下のように潜在変数\(z_q\)を表します。したがって、各ピクセルはK種類のベクトルで表現されます。
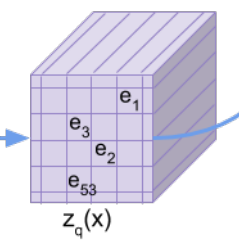
そして、得られた潜在変数からデコーダで画像を復元します。
離散潜在変数
エンコーダ・デコーダ部分は一般的なCNNを使いますので説明は省略しますが、VQ-VAEの特徴である埋め込み表現の説明をしたいと思います。
先ほど出てきた潜在変数の埋め込み表現空間を\(e\in\mathbb{R}^{K\times D}\)とします。
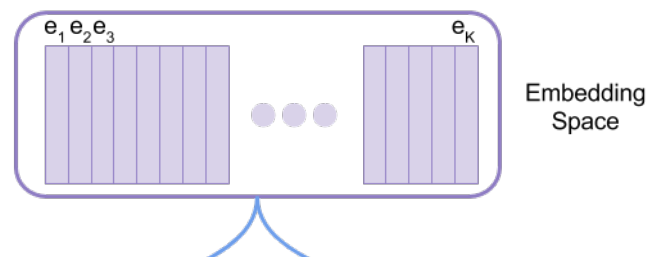
\(K\)は埋め込み表現の種類、\(D\)は埋め込み表現の次元を表します。
つまり、\(K\)個の埋め込み表現の中から、画像の各位置に対応する埋め込み表現を一つ選びます。
32x32の画像であれば、322箇所決める必要があります。
では、各位置について、どうやって埋め込み表現を選ぶのでしょう?
それは、エンコーダで計算した\(z_e(x)\)ともっとも距離が近い埋め込み表現を選びます。
数式で書くと、\(z=k\)となる確率\(q(z|x)\)は、
$$\begin{align}
q(z=k|x)=\left\{\begin{array}{ll}1&\text{for }k=\arg \min_j \| z_e(x)-e_j \|_2, \\ 0&\text{otherwise}\end{array}\right.
\end{align}$$
となります。
距離によって確定的に決まりますので、確率は1か0です。
そして、デコーダのインプットである\(z_q(x)\)は選ばれた\(k\)番目の埋め込み表現を使います。
$$z_q(x)=e_k, \hspace{10pt}\text{where } k=\arg\min_j\|z_e(x)-e_j\|_2$$
学習
ここまでは比較的シンプルだと思います。
ただ、少し厄介なのは上述の通り\(\arg\min\)を取ってしまうと、学習時に勾配が計算できなくなってしまう点です。
VAEのときにも勾配が計算できなくなりましたが、Reparameterization Trick(再パラメータ化)によってうまく回避していました。
しかしながら、Reparameterization Trickは連続変数でしか使えません。
Reparameterization Trickの離散版とも言えるContinuous Relaxationといった手法もありますが、VQ-VAEではもっとシンプルに近似します。
簡単に言うと、下の図の赤い線のように、埋め込み表現を選ぶ部分を飛ばします。
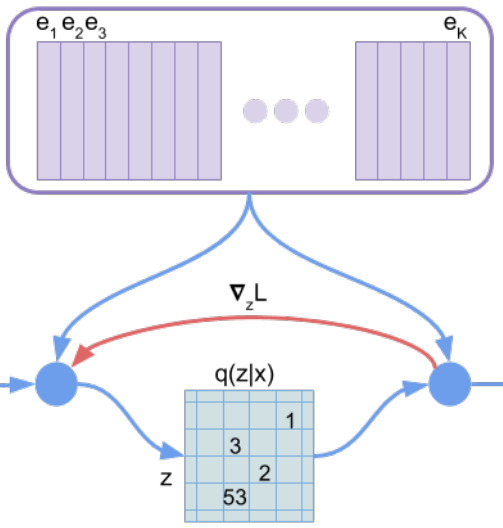
つまり、\(z_e\)から\(z_q\)を計算するところに\(\arg\min\)のオペレーションが入っているので、\(\frac{\partial z_q}{\partial z_e}\)が計算できないのですが、これを
$$\frac{\partial z_q}{\partial z_e}\approx 1$$
としてしまいます。
ですので、
$$\frac{\partial L}{\partial z_e}=\frac{\partial L}{\partial z_q}\frac{\partial z_q}{\partial z_e}\approx \frac{\partial L}{\partial z_q}$$
として、勾配がそのまま流れていくことになります(これをstreight estimatorと呼びます)。
損失関数
損失関数は以下とします。
$$L=\log p\left(x|z_q(x)\right) + \left\|\text{sg}[z_e(x)]-e \right \|^2_2 + \beta \left\|z_e(x)-\text{sg}[e]\right\|^2_2$$
見てわかる通り、3つの項に分かれています。
1項目は再構築誤差です(後で出てくる実装では二乗誤差を使っています)。
2項目は埋め込み表現を更新するための誤差項になります。
\(\text{sg}\)はバック・プロパゲーション時に勾配を計算しない(stop gradient)という意味のオペレータです。
上で出てきたように、
$$\frac{\partial z_q}{\partial z_e}\approx 1$$
とすることで勾配を流していきましたが、このようにすることで、埋め込み表現\(e\)のテーブルが更新されなくなります。
そこで、この項を導入することにより\(z_e\)と\(e\)を近くする形で埋め込み表現を更新します。
論文では指数移動平均(Exponential Moving Average; EMA)を使って、埋め込み表現を更新する方法も説明されていますが、ここでは省略させていただきます。
興味がある方は論文をご参照ください。
3項目は、エンコーダーのアウトプット\(z_e\)が埋め込み表現\(e\)に対して、先にどんどん更新されないようにする項になります。
\(\beta\)は本論文では0.25にしています。
ところで、周辺尤度ではなく、下界を最大化するのがVAEでした。
そして、下界は
$$\mathcal{L}({\bf{x}}, \phi, \theta)= \mathbb{E}_{q_\phi({\bf{z}}|{\bf{x}})}\left[\log p_\theta({\bf{x}}|{\bf{z}})\right] -D_{KL}\left( q_\phi({\bf{z}}|{\bf{x}})||p_\theta({\bf{z}}) \right)$$
という形で、再構築誤差の項とKLダイバージェンスの項に分かれており、これらを足したもので表されました。
VQ-VAEではKLダイバージェンス項がありません。
この理由は、\(z\)の事前分布に一様分布を仮定しているためKLダイバージェンス項が定数になり無視できるからです。
一応、KLダイバージェンス項が定数になることを見ておきましょう。
$$\begin{align}
D_{KL}\left(q(z|x)||p_\theta(z) \right) &= \sum_z q(z|x)\log \frac{q(z|x)}{p(z)} \\
&=-\sum_z q(z|x)\log p(z) + \sum_z q(z|x)\log q(z|x) \\
&=-\sum_z q(z|x)\log \frac{1}{K} + \sum_z q(z|x)\log q(z|x) \\
&= \log K
\end{align}$$
2行目から3行目は、\(p(z)=1/K\)を使っています。
3行目から4行目は、\(q(z|x)\)が確定的なのでどこかの1点で1を取ることを使っています。
ということで、VQ-VAEの学習ではKLダイバージェンス項は存在しません。
事前分布
事前分布\(p(z)\)は\(z\)が\(K\)種類の離散的な値(ベクトル)を取るので、カテゴリカル分布を使います。
上述の通り、学習時は\(p(z)\)を一様分布、つまり\(p(z_k)=\frac{1}{K}\)とします。
ただ、学習後にデータを生成する際に、一様分布から\(z\)をサンプリングすると、うまく画像が生成できません。
本来\(z\)には何らかのパターンがあり、それを表現する必要があると思われます。
そこで、VQ-VAEでは、学習後に画像データを生成する際には、\(p(z)\)をPixelCNNに学習させ、それを使って\(z\)を生成します(PixelCNNはこちらをご参照ください『Conditional Image Generation with PixelCNN Decoders』)。
PixelCNNも画像の生成モデルで、潜在変数を使わないモデルです。
また、音声の場合はWaveNetを使います。
画像の場合ですと、まず学習済みのVQ-VAEを使って潜在変数(カテゴリ)\(z\)を計算します。
その\(z\)に対してPixelCNNを学習することで、事前分布を学習することができます。
そして、学習済みのPixelCNNで潜在変数\(z\)を生成し、それをもとに学習済みのVQ-VAEで画像を生成するという仕組みです。
実験
VQ-VAEモデルの設定
エンコーダ、デコーダともに畳み込みニューラル・ネットワーク(Convolutional Neural Network; CNN)を使います。
具体的には、エンコーダは、インプットから4x4、ストライドが2の畳み込みレイヤーを2つ、そして、3x3の畳み込みレイヤー、1x1の畳み込みレイヤからなる残差ブロックを2つ続けます。
隠れ層の次元は、256です。
埋め込み表現の種類\(K\)は512とします。
デコーダは、3x3の残差ブロックを2個、そして、4x4のストライドが2の転地畳み込みレイヤーを2つ続けます。
オプティマイザは学習率を2e-4としたADAMを使います。
詳細は実装のところを見ていただいた方が早いと思います。
結果
精度比較
VQ-VAEとVAE、VIMCO(論文はこちら『Variational inference for Monte Carlo objectives』)をbits/dimで比較します。
bits/dimは画像の次元数で正規化した負の対数尤度のようなイメージですので、小さいほど精度が良い指標です。
結果は、VQ-VAEが4.67 bits/dim、VAEが4.51 bits/dim、VIMCOが5.14 bits/dimとなり、VAEが一番良く、VQ-VAEがそのあとに続いています。
ということで、VAEには及びませんでしたが、VAEに遜色のない結果となっています。
画像の再構築
ここでは、ImageNetの128x128x3の画像をVQ-VAEにより、32x32x1の次元に圧縮し、そこから元の画像の再構築を行います。
128x128x3x8ビット(256が28だから)から、32x32x1x9ビット(512=29より)に圧縮していますので、\(\frac{128\times 128\times 3\times 8}{32\times 32\times 9}\simeq 42.6\)ビットの減少ということになります。
再構築した結果がこちらです。

うまくいっていますね。
次は画像の生成です。
ImageNetデータセットを使って、VQ-VAEによる潜在変数\(z\)の分布を(conditional)PixelCNNに学習させます。
そして、PixelCNNで新たに生成した潜在変数をもとにVQ-VAEで画像を生成した結果が以下です。

conditional PixelCNNを使っているので、ラベルを与えることで、そのラベルに従って潜在変数を生成することが可能です。
一番左から、こどものキツネ、灰色のくじら、茶色の熊、アカタテハ蝶、サンゴ礁、アルプス、電子レンジ、小型トラック(車?)、となっています。
よくわからない画像もありますが、雰囲気は出ていますね。
続いて、DeepMind Labの3D画像(動画を画像にしたもの)についても同様にPixelCNNで学習した事前分布をもとに画像を生成しています。

こちらはイメージ通りですね。
この他にも音声データやDeepMind Labの3D動画の結果も載っていますので、興味のある方は論文をご参照いただければと思います。
VQ-VAEの実装
では、最後にTensorflowを使ってVQ-VAEを実装していきたいと思います。
PyTorchの実装は以下の記事で行っていますので、参考にしてみてください。
実装は以下を参考にしています。sonnetというDeepMind社のライブラリを使用していますが、ここではsonnetは使わないように修正しています。
https://github.com/deepmind/sonnet/blob/v2/examples/vqvae_example.ipynb
なお、ここではMoving Averageを使う方は実装していません。
興味がある方は、以下のコードを参考にしていただければと思います。
https://github.com/deepmind/sonnet/blob/v2/sonnet/src/nets/vqvae.py
では、まずは、必要なパッケージのインポートです。
import matplotlib.pyplot as plt import numpy as np import tensorflow as tf import tensorflow_datasets as tfds
続いて、CIFAR10をTensorflowのデータセットからダウンロードします。
cifar10 = tfds.as_numpy(tfds.load("cifar10:3.0.2", split="train+test", batch_size=-1))
cifar10.pop("id", None)
cifar10.pop("label")
fig, ax = plt.subplots(nrows=5, ncols=5, figsize=(5, 5))
for i in range(25):
idx = divmod(i, 5)
ax[idx].imshow(cifar10['image'][i])
ax[idx].axis('off');
このような画像が出てきます。

では、残差結合の部分を作成します。
インプットを、3x3、1x1の畳み込み層で処理をし、残差結合を行っています。
パラメータは隠れ層の次元(ここでは128次元)、残差結合層を繰り返す回数(ここでは2回)、残差結合層の隠れ層の次元(ここでは32)です。
paddingは“same”として、サイズを変えないようにしましょう。
class ResidualStack(tf.keras.layers.Layer):
def __init__(self, hidden_dim, num_layers, residual_hidden_dim, name=None):
super(ResidualStack, self).__init__(name=name)
self._hidden_dim = hidden_dim
self._num_layers = num_layers
self._residual_hidden_dim = residual_hidden_dim
self._layers = []
for i in range(num_layers):
conv3 = tf.keras.layers.Conv2D(filters=residual_hidden_dim,
kernel_size=3,
strides=(1, 1),
padding='same',
name=f'res3x3_{i:d}'
)
conv1 = tf.keras.layers.Conv2D(filters=hidden_dim,
kernel_size=1,
strides=(1, 1),
padding='same',
name=f'res1x1_{i:d}'
)
self._layers.append((conv3, conv1))
def __call__(self, inputs):
h = inputs
for conv3, conv1 in self._layers:
conv3_out = conv3(tf.nn.relu(h)) # 3x3 conv layer
conv1_out = conv1(tf.nn.relu(conv3_out)) # 1x1 conv layer
h += conv1_out # 残差結合
return tf.nn.relu(h)
続いて、エンコーダです。
エンコーダは、4x4(stride 2)、4x4(stride 2)、3x3(stride 1)の畳み込み層で処理をし、先ほど作成した残差結合層に渡します。
各レイヤにはReLUを挟みます。
パラメータは残差結合層と同じです。
class Encoder(tf.keras.layers.Layer):
def __init__(self, hidden_dim, num_residual_layers, residual_hidden_dim, name=None):
super(Encoder, self).__init__(name=name)
self._hidden_dim = hidden_dim
self._num_residual_layers = num_residual_layers
self._residual_hidden_dim = residual_hidden_dim
self._enc_1 = tf.keras.layers.Conv2D(
filters=hidden_dim // 2, # channelを半分に
kernel_size=4,
strides=(2, 2),
padding='same',
name='enc_1'
)
self._enc_2 = tf.keras.layers.Conv2D(
filters=hidden_dim,
kernel_size=4,
strides=(2, 2),
padding='same',
name='enc_2'
)
self._enc_3 = tf.keras.layers.Conv2D(
filters=hidden_dim,
kernel_size=3,
strides=(1, 1),
padding='same',
name='enc_3'
)
self._residual_stack = ResidualStack(
hidden_dim,
num_residual_layers,
residual_hidden_dim,
name='enc_res_stack')
def __call__(self, inputs):
h = tf.nn.relu(self._enc_1(inputs))
h = tf.nn.relu(self._enc_2(h))
h = self._enc_3(h)
return self._residual_stack(h)
デコーダもほぼ同じです。
畳み込み層ではなく、転地畳み込み層を使って、サイズを大きくしていきます。
3x3(stride 1)の畳み込み層、残差結合層、4x4(stride 2)、4x4(stride 2)の畳み込み層と処理をします。
こちらもパラメータは残差結合層、エンコーダと同じです。
class Decoder(tf.keras.layers.Layer):
def __init__(self, hidden_dim, num_residual_layers, residual_hidden_dim,
name=None):
super(Decoder, self).__init__(name=name)
self._hidden_dim = hidden_dim
self.num_residual_layers = num_residual_layers
self.residual_hidden_dim = residual_hidden_dim
self._dec1 = tf.keras.layers.Conv2D(
filters=hidden_dim,
kernel_size=3,
strides=(1, 1),
padding='same',
name='dec_1'
)
self._residual_stack = ResidualStack(
hidden_dim,
num_residual_layers,
residual_hidden_dim,
name='dec_res_stack')
self._dec2 = tf.keras.layers.Conv2DTranspose(
filters=hidden_dim // 2,
kernel_size=4,
strides=(2, 2),
padding='same',
name='dec_2'
)
self._dec3 = tf.keras.layers.Conv2DTranspose(
filters=3,
kernel_size=4,
strides=(2, 2),
padding='same',
name='dec_3'
)
def __call__(self, encoder_outputs):
h = self._dec1(encoder_outputs)
h = self._residual_stack(h)
h = tf.nn.relu(self._dec2(h))
x_reconstructed = self._dec3(h)
return x_reconstructed
では、重要なVectorQuantizer層です。
input_flattenedに32x32x embedding_dimのインプットを322x embedding_dimにしたものを設定することで、並列計算を行っています。
distanceに距離の2乗を設定し(うまく工夫された実装です)、その距離が最も小さいインデックスをencoding_indicesに入れます。
そして、quantizeメソッドでそのインデックスに対応する埋め込み表現を取ってきます。
その後、上述の損失関数を計算しています。“_commitment_cost”が論文の\(\beta\)に当たります。
quantizedという変数が\(z_q\)に当たりますが、\(z_q\)から\(z_e\)に勾配を流さないようように“inputs + tf.stop_gradient(quantized - inputs)”としています。
class VectorQuantizer(tf.keras.layers.Layer):
def __init__(self, embedding_dim, num_embeddings, commitment_cost,
name='vq_layer'):
super(VectorQuantizer, self).__init__(name=name)
self._embedding_dim = embedding_dim
self._num_embeddings = num_embeddings
self._commitment_cost = commitment_cost
initializer = tf.keras.initializers.RandomUniform()
w_init = tf.random_normal_initializer()
self._w = tf.Variable(
initial_value=w_init(shape=(embedding_dim, num_embeddings), dtype='float32'),
trainable=True)
def __call__(self, inputs, is_training):
input_shape = tf.shape(inputs)
input_flattened = tf.reshape(inputs, [-1, self._embedding_dim])
distances = (tf.reduce_sum(input_flattened ** 2, 1, keepdims=True)
- 2 * tf.matmul(input_flattened, self._w)
+ tf.reduce_sum(self._w ** 2, 0, keepdims=True))
encoding_indices = tf.argmax(-distances, 1)
encodings = tf.one_hot(encoding_indices, self._num_embeddings)
encoding_indices = tf.reshape(encoding_indices, tf.shape(inputs)[:-1]) # 元のshapeに合わせる
quantized = self.quantize(encoding_indices)
e_latent_loss = tf.reduce_mean(tf.square(tf.stop_gradient(quantized) - inputs))
q_latent_loss = tf.reduce_mean(tf.square(quantized - tf.stop_gradient(inputs)))
loss = q_latent_loss + self._commitment_cost * e_latent_loss
quantized = inputs + tf.stop_gradient(quantized - inputs)
return {'distances': distances,
'quantize': quantized,
'loss': loss,
'encodings': encodings,
'encoding_indices': encoding_indices}
def quantize(self, encoding_indices):
w = tf.transpose(self._w, [1, 0])
return tf.nn.embedding_lookup(w, encoding_indices)
最後に作成したレイヤーをまとめて、VQVAEクラスを作成します。
class VQVAE(tf.keras.Model):
def __init__(self, encoder, decoder, vqvae, pre_vq_conv1,
data_variance, name=None):
super(VQVAE, self).__init__(name=name)
self._encoder = encoder
self._decoder = decoder
self._vqvae = vqvae # Conv2D(output_channels=embedding_dim, 1x1)
self._pre_vq_conv1 = pre_vq_conv1
self._data_variance = data_variance
def __call__(self, inputs, is_training):
z = self._pre_vq_conv1(self._encoder(inputs)) # zの事前分布
vq_output = self._vqvae(z, is_training=is_training)
x_reconstructed = self._decoder(vq_output['quantize'])
reconstructed_error = tf.reduce_mean(tf.square(x_reconstructed - inputs) / self._data_variance)
loss = reconstructed_error + vq_output['loss']
return {
'z': z,
'x_reconstructed': x_reconstructed,
'loss': loss,
'reconstructed_error': reconstructed_error,
'vq_output': vq_output
}
では、データセットを作成しましょう。
まず、学習データと検証データに分割します。
train_data = cifar10['image'][:40000] val_data = cifar10['image'][40000:50000]
データを正規化してデータセットを作成します。
def cast_and_nomrmalise_images(images):
return (tf.cast(images, tf.float32) / 255.0) - 0.5
train_dataset = (
tf.data.Dataset.from_tensor_slices(train_data)
.map(cast_and_nomrmalise_images)
.shuffle(10000)
.repeat(-1)
.batch(BATCH_SIZE, drop_remainder=True)
.prefetch(-1)
)
val_dataset = (
tf.data.Dataset.from_tensor_slices(val_data)
.map(cast_and_nomrmalise_images)
.repeat(1)
.batch(BATCH_SIZE)
.prefetch(-1)
)
ハイパーパラメータを設定します。
BATCH_SIZE = 32 IMAGE_SIZE = 32 NUM_OF_TRAINING_UPDATES = 10000 HIDDEN_DIM = 128 RESIDUAL_HIDDEN_DIM = 32 NUM_RESIDUAL_LAYERS = 2 EMBEDDING_DIM = 64 # 各埋め込み表現は64次元 NUM_EMBEDDINGS = 512 # いわゆるK. K種類の埋め込み表現がある COMMITMENT_COST = 0.25 # βのこと LEARNING_RATE = 3e-4
では、モデルのインスタンスを作成しましょう。
エンコーダ、デコーダなどのレイヤのインスタンスを作成し、VQVAEクラスに渡してやります。
train_data_variance = np.var(train_data / 255.0)
encoder = Encoder(hidden_dim=HIDDEN_DIM,
num_residual_layers=NUM_RESIDUAL_LAYERS,
residual_hidden_dim=RESIDUAL_HIDDEN_DIM)
decoder = Decoder(hidden_dim=HIDDEN_DIM,
num_residual_layers=NUM_RESIDUAL_LAYERS,
residual_hidden_dim=RESIDUAL_HIDDEN_DIM)
pre_vq_conv1 = tf.keras.layers.Conv2D(filters=EMBEDDING_DIM,
kernel_size=1,
strides=1,
padding='same',
name='to_vq')
vqvae = VectorQuantizer(
embedding_dim=EMBEDDING_DIM,
num_embeddings=NUM_EMBEDDINGS,
commitment_cost=COMMITMENT_COST,
)
# モデル
model = VQVAE(encoder=encoder,
decoder=decoder,
vqvae=vqvae,
pre_vq_conv1=pre_vq_conv1,
data_variance=train_data_variance)
オプティマイザはアダムを使います。
# オプティマイザ optimizer = tf.keras.optimizers.Adam(learning_rate=LEARNING_RATE)
学習用の関数を作成します。
@tf.function
def train_step(data):
with tf.GradientTape() as tape:
model_output = model(data, is_training=True)
trainable_variables = model.trainable_variables
grads = tape.gradient(model_output['loss'], trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return model_output
では、実際に学習してみます。
train_losses, train_recon_errors, train_perplexities, train_vqvae_loss = [], [], [], []
for i, data in enumerate(train_dataset):
train_results = train_step(data)
train_losses.append(train_results['loss'])
train_recon_errors.append(train_results['reconstructed_error'])
train_vqvae_loss.append(train_results['vq_output']['loss'])
if (i + 1) % 100 == 0:
print('%d train loss: %f ' % (i + 1,
np.mean(train_losses[-100:])) +
('recon_error: %.3f ' % np.mean(train_recon_errors[-100:])) +
('vqvae loss: %.3f' % np.mean(train_vqvae_loss[-100:])))
if i == NUM_OF_TRAINING_UPDATES:
break
これで学習ができました。
では、結果を見てみましょう。
validationデータについて、オリジナルの画像と再構成した画像が以下になります。

うまくいっていいそうですね!
まとめ
今回は、VAE(Variational AutoEncoder)の潜在変数を離散的な埋め込み表現にしたVQ-VAE(Vector Quantised-Variational AutoEncoder)を見てきました。
そういえばこちらは、OpenAIのDALL-Eなどでも使われている技術ですね。
また、今度はPixelCNNを使って\(z\)の事前分布を学習し、画像を生成してみたいと思います。
では!!


