さて、今回は画像の生成モデルの一つであるPixelCNNを解説し、最後にPyTorchで簡単に実装していきたいと思います。
PixelCNNは、まず2016年に以下の論文でPixelRNNなどとともに提案された画像の生成モデルです。
『Pixel Recurrent Neural Networks』
画像の分布を学習し、新たな画像を生成するモデルで、GAN(Generative Adversarial Network)やVAE(Variational AutoEncoder)などと同じ用途になります。
GANやVAEと違う点は、PixelCNNは次のピクセル、次のピクセルという形で再帰的に次のピクセルの値を予測することで(Auto-Regressive)画像の分布を学習する点です。
自然言語処理を学習した人には、この再帰的に次を予測するというのは馴染みがあるかもしれませんね。
自然言語処理では、「私」の次の単語は、「は」、その次は…という形で文章を学習することで、言語モデルを獲得する方法があります。
その画像版と考えてよいかと思います。
そして、PixelCNNでは内部の仕組みに畳み込みニューラルネットワーク(CNN)を使いますが、CNNではなくTransformerを使うことにより、OpenAIのImageGPTへとつながってきます。
また、続けて以下の論文で、クラスの情報で条件付けした場合のConditional PixelCNNを提案されています。
『Conditional Image Generation with PixelCNN Decoders』
これにより、「犬」や「猫」というクラスを与えて、そのクラスの画像を生成することが可能になります。
今回はConditional PixelCNNではなく、シンプルなPixelCNNについて実装していきたいと思います。
目次
PixelCNNとは
PixelCNNは、次のピクセル、次のピクセルという形で再帰的にピクセルの値を予測することで(Auto-Regressive)、直接画像の分布を学習する画像の生成モデルです。
具体的には、画像のピクセルに対し、左上から順番に次のピクセルの値を予測するように学習します。
まず、左上の\(x_1\)を予測し、次に\(x_1\)の値を使って\(x_2\)を予測します。
次に\(x_1\)と\(x_2\)の値を使って\(x_3\)を予測します。
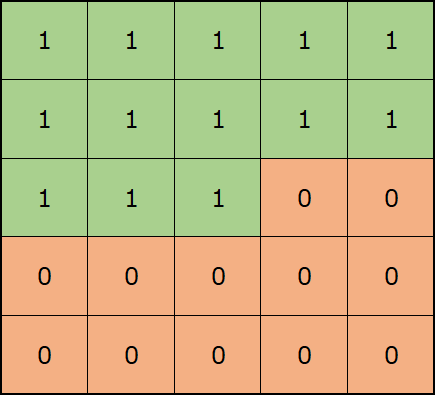
以下の図は、これを続けて、\(x_1\)から\(x_{i-1}\)の情報を使って\(x_i\)を予測する場合のイメージです。
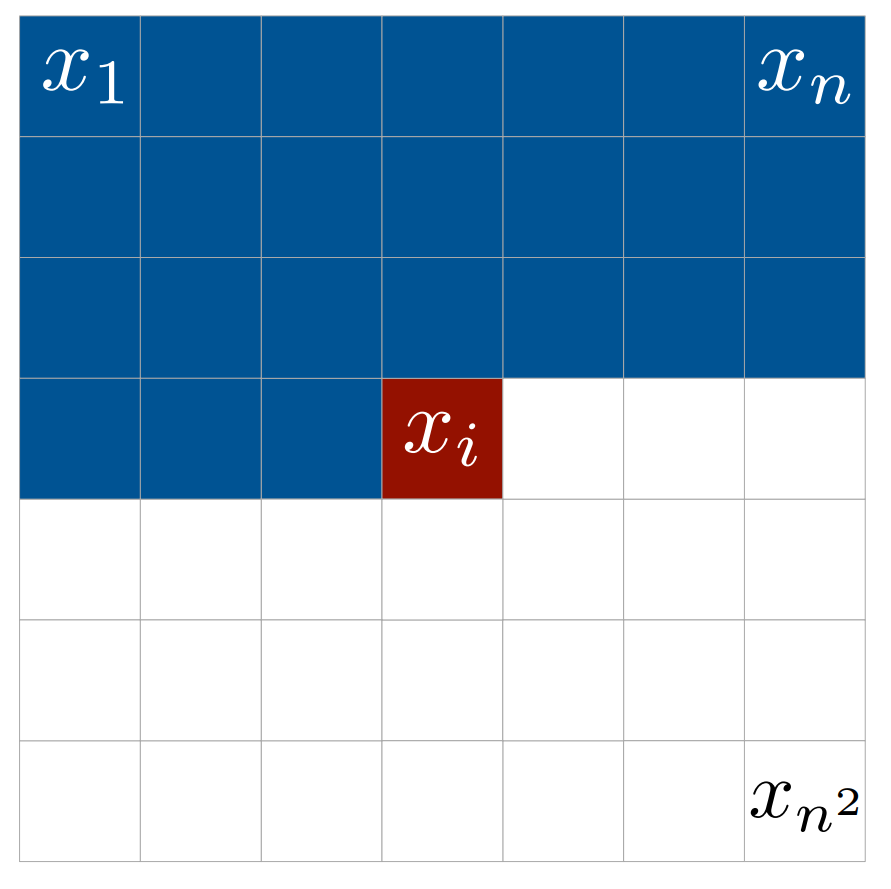
数式で表すと、解像度が\(n\)x\(n\)の白黒画像の場合、画像の同時分布は以下の式で表されます。
$$p({\bf{x}})=p(x_1,\cdots,x_{n^2})$$
これを条件付き確率の形で書くと、
$$p({\bf{x}})=\prod_{i=1}^{n^2} p(x_i|x_1,\cdots,x_{i-1})$$
のように条件付き期待値の積で表されます。
PixelCNNは、この形で学習します。
なお、カラー画像であればこれにRGBのチャネルが追加されるので、もう少し複雑になりますが、考え方は同じなので1チャネルの場合で説明します。
そして、PixelCNNは名前の通りCNN(Convolutional Neural Network)を使ってモデル化します。
論文ではPixelRNNというモデルも提案されており、こちらはCNNではなくピクセルが時系列に並んでいるととらえて、RNN(Recurrent Neural Network)を使って処理をします。
マスク
PixelCNNでは、前のピクセルから順番に予測していくので、上の図の\(x_i\)の値を予測する際に見ていいのは\(x_{i-1}\)までです。
しかしながら、普通の畳み込み処理をしてしまうと、自分の情報や自分よりあとの情報も使ってしまいます。
そこで、PixelCNNでは通常の畳み込みレイヤではなく、マスクをした畳み込みレイヤを使います。
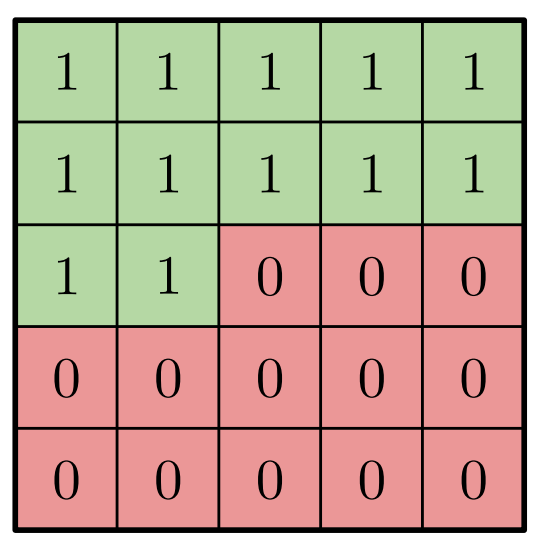
以下の図のように、自分自身を含めて先を使わないように(見ないように)マスクをします。
5x5の畳み込みフィルタの場合のマスクは以下のようになります。0はマスクをすることにより情報を使わない位置です。中央が自分自身の位置に対応します。
このマスクを畳み込みフィルタにかけることによって、自分自身と先を見ない畳み込み演算が可能になります。
数式で書くと以下のようになります。
$$\begin{align}
x^{(i+1)} = g((W^{(i)}\times {mask})*x^{(i)})
\end{align}$$
\(*\)は畳み込み演算、\(g\)はtanhやReLUといった活性化関数を表し、\(i\)は\(i\)番目のレイヤであることを表しています。
\(W\)が畳み込みフィルタになります。
そして、最終的には各ピクセルの位置にある0から255の数値を予測していきます。
(余談) ImageGPT
余談ですが、ImageGPTではこれを畳み込みではなく、Transformerを使って処理を行います。
Transformerの非常に高い柔軟性と,
より大規模なデータを使うことにより、非常に精度の高い画像を生成することができるようになっています。
ImageGPTが生成した画像が以下です。
一番左の画像をインプットし、黒く塗りつぶされている部分を生成しています。

ImageGPTの解説はこちらにありますので、興味がある方はご参照ください。
マスク付き畳み込み処理の詳細
では、PixelCNNのキーポイントとなるマスク付き畳み込み処理について詳しく説明していきます。
2種類のマスク付き畳み込み処理があります。
マスクA … 自分自身の位置を含めて先を見ない
一つ目は、自分自身を含め先を見ないマスクです。これを論文ではマスクAと呼んでいます。
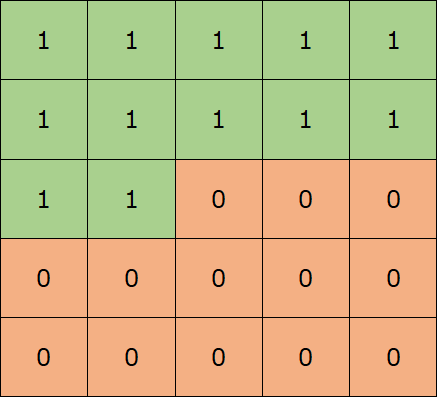
マスクB ... 自分自身の位置は見ることができる
もう一つは、上述の自分自身は見れますが、先は見れないマスクです。これを論文ではマスクBと呼んでいます。
使い分け
当然、\(i\)番目の位置の予測に\(x^{input}_i\)の情報は使ってはいけませんので、一番初めのレイヤについてはマスクAを使います。
そのため、初めのレイヤでマスクAを使って畳み込んだあとの、\(i\)番目の位置の値\(x^{(2)}_i\)には\(x^{input}_i\)の情報は含まれていません。
ですので、2番目のレイヤからはこの\(i\)番目の情報を使っても問題ありません。
むしろ使わないといけませんね(実装のときにうっかりマスクAを使ってしまっていたことに気づかず、精度が上がらないので困ってしまいました)。
ということで、2番目以降のレイヤについてはマスクBを使います。
ゲート付きPixelCNN
ゲート付きPixelCNNは、再帰的ニューラル・ネットワーク(RNN)におけるLSTM(Long Short-Term Memory)やGRU(Gated Recurrent Unit)のように直前の情報を次に流すかどうかを学習するゲートを導入することで、精度を高めようとしたモデルです。
$$\begin{align}
x^{(i+1)} = g\left(W_{f, i}*x^{(i)}\odot sigmoid(W_{g, i}*x^{(i)})\right)
\end{align}$$
と表されます。マスクは省略しています。
\(sigmoid(W_{g, i}*x^{(i)})\)はゲートを表し、情報を流す場合は1に近く、流さない場合は0に近くなります。
\(\odot\)は要素ごとの積を表します。
条件付きPixelCNN
クラスを指定して画像を生成するのが条件付きPixelCNNです。
この場合はクラスの情報を渡します。
ゲート付き、条件付きPixelCNNの場合では、\(h\)をクラスを表す潜在変数として、
$$\begin{align}
x^{(i+1)} = \left(g(W_{f, i}*x^{(i)}+V^T_{f, k}h\right)\odot \left(sigmoid(W_{g, i}*x^{(i)}+V^T_{g, k}h \right)
\end{align}$$
で表されます。
実装
今回は、単純なPixelCNNを実装したいと思います。
次回ゲートや条件付きのPixelCNNを実装する予定です。
なお、ソースコードはこちらを参考にしています。
では、実装していきましょう。
とりあえず必要なモジュールをインポートしておきます。
import matplotlib.pyplot as plt import numpy as np import torch import torch.nn.functional as F from torch import nn, optim from torch.utils import data from torchvision import datasets, transforms, utils
マスク付き畳み込み層
まず、一番重要なマスク付き畳み込み層を作成します。
class MaskedConv2d(nn.Conv2d):
def __init__(self, mask_type, *args, **kwargs):
super(MaskedConv2d, self).__init__(*args, **kwargs)
assert mask_type in ['A', 'B']
self.register_buffer('mask', self.weight.data.clone())
h = self.weight.size()[2]
w = self.weight.size()[3]
self.mask.fill_(1)
# マスクタイプによる場合分け
if mask_type == 'A': # 自分自身も見ない
self.mask[:, :, h // 2, w // 2:] = 0
self.mask[:, :, h // 2 + 1:] = 0
else: # 自分自身は見る
self.mask[:, :, h // 2, w // 2 + 1:] = 0
self.mask[:, :, h // 2 + 1:] = 0
def forward(self, x):
self.weight.data *= self.mask
return super(MaskedConv2d, self).forward(x)
畳み込みフィルタの重みをゼロにする必要があるので、5行目でマスクを作成しています。
register_bufferで、モデルパラメータではない変数として、マスクを定義しています。
高さ\(h\)、幅\(w\)の畳み込みフィルタであれば、真ん中より左上には1を設定し、それよりも右下であれば0を設定しています。
mask_typeがAであれば11行目で自分自身の位置も見ないようにマスクの範囲を設定し、Bであれば14行目で自分自身の位置は見れるように設定しています。
あとは、18行目で畳み込みフィルタのウェイトにマスクをかけて、畳み込み処理を行っています。
モデル全体
以下がPixelCNNの全体です。
class PixelCNN(nn.Module):
def __init__(self, num_of_channels=32, n_layers=7, output_channels=256):
super(PixelCNN, self).__init__()
self.layers = nn.ModuleList()
# 最初のブロック
self.layers.append(MaskedConv2d(mask_type='A',
in_channels=1,
out_channels=num_of_channels,
kernel_size=7,
stride=1,
padding=3,
bias=False))
self.layers.append(nn.BatchNorm2d(num_of_channels))
self.layers.append(nn.ReLU(inplace=True))
# 後続のブロック
for i in range(1, n_layers+1):
self.layers.append(MaskedConv2d(mask_type='B',
in_channels=num_of_channels,
out_channels=num_of_channels,
kernel_size=7,
stride=1,
padding=3,
bias=False))
self.layers.append(nn.BatchNorm2d(num_of_channels))
self.layers.append(nn.ReLU(inplace=True))
self.layers.append(nn.Conv2d(in_channels=n_channels,
out_channels=output_channels,
kernel_size=1))
def forward(self, x):
out = x
for layer in self.layers:
out = layer(out)
return out
nn.ModuleList()にレイヤを追加していきます。
初めはタイプAのマスク付き畳み込み層から、バッチ正規化層、ReLUによる活性化関数と処理します。
その次からタイプBのマスク付き畳み込み層、バッチ正規化層、ReLUによる活性化関数という処理を7回繰り返します。
最後に、1x1の畳み込み処理を使って、255個のチャネル(output_channels)の形で出力します。
データセットの読み込み
データセットは簡単にMNISTを使いましょう。
trainloader = data.DataLoader(datasets.MNIST('data', train=True,
download=True,
transform=transforms.ToTensor()),
batch_size=128, shuffle=True,
num_workers=1, pin_memory=True)
testloader = data.DataLoader(datasets.MNIST('data', train=False,
download=True,
transform=transforms.ToTensor()),
batch_size=128, shuffle=False,
num_workers=1, pin_memory=True)
学習
では、学習です。
レイヤ数やエポック数などを設定しています。
num_of_layers = 7 # 畳み込み層の数 num_of_channels = 64 # チャネル数 num_of_epochs = 50 X_DIM = 28 NUM_OF_VALUES = 255 device = 'cuda:0'
モデルをインスタンス化します。
pixel_cnn = PixelCNN(n_channels, num_of_layers).to(device)
では、あとは学習するだけです。
optimizer = optim.Adam(list(pixel_cnn.parameters()))
criterion = nn.CrossEntropyLoss()
train_losses, test_losses = [], []
for epoch in range(num_of_epochs):
# 学習
train_errors = []
pixel_cnn.train()
for x, label in trainloader:
x = x.to(device)
target = (x[:,0] * num_of_output_values).long()
loss = criterion(pixel_cnn(x), target)
train_errors.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 評価
with torch.no_grad():
teset_errors = []
pixel_cnn.eval()
for x, label in testloader:
x = x.to(device)
target = (x[:,0] * num_of_output_values).long()
loss = criterion(pixel_cnn(x), target)
teset_errors.append(loss.item())
print(f'epoch: {epoch}/{num_of_epochs} train error: {np.mean(train_errors):0.3f} \
test error {np.mean(test_errors):0.3f}')
train_losses.append(np.mean(train_errors))
test_losses.append(np.mean(test_errors))
以上でプログラムは作成完了です。ここの処理はPyTorchの通常の処理なので、詳細の解説は省略します。
では、学習した結果を見てみましょう。
以下のコードで画像を生成します。
sample = torch.Tensor(25, 1, X_DIM, X_DIM).to(device)
pixel_cnn.eval()
sample.fill_(0)
for i in range(X_DIM):
for j in range(X_DIM):
out = pixel_cnn(sample).to(device)
probs = F.softmax(out[:, :, i, j], dim=1)
sample[:, :, i, j] = torch.multinomial(probs, 1).float() / NUM_OF_VALUES
sample_array = sample.cpu().numpy().squeeze()
fig, ax = plt.subplots(nrows=5, ncols=5, figsize=(5, 5))
for i in range(25):
idx = divmod(i, 5)
ax[idx].imshow(sample_array[i]*255, cmap='gray')
ax[idx].axis('off');
fig.show()
4行目から8行目のループ処理で左上から順番にピクセルの値を予測しています。
以下が生成された画像です。

数字に見えるものもありますが、見えないものも多く、精度が高いとは言えませんね…
ちなみに同じ生成モデルであるVAEでは以下のような画像が生成されるので、この段階ではVAEの方がいいですね。しかもVAEは非常に軽量です。

VAEについては以下の記事をご参照ください(ちょっと細かいところまで解説しすぎていますが…)。
もう少しチューニングすればよくなると思いますが、今後ゲート付きPixelCNNやConditional PixelCNNを実装していく予定ですので、いったんはこちらでおいておきたいと思います。
まとめ
今回は画像の生成モデルであるPixelCNNを見てきました。
まだ、それほど使えるようには見えませんが、これからゲート付きPixelCNNやConditional PixelCNNを見ていきたいと思います。
さらにattentionを使ったPixelSnailといったモデルなどに発展していきますので、今回見てきたPixelCNNはその基本形になっています。
VQ-VAEなどでも使われていますので、今回の解説でPixelCNNのイメージを掴んでいただけたらうれしいです。
では!

