これまでVAE(Variational Auto-Encoder)やVQ-VAE(Vector-Quantized VAE)について解説しましたが、今回はGANとも並ぶ精度を実現したVQ-VAE2(Vector Quantized-Variational Auto-Encoderについて解説したいと思います。
VAEはGAN(Generative Adversarial Network)と比べると画像がぼやけるという質の問題がありましたが、VAEからVQ-VAE、さらにVQ-VAE2と進化して、以下の画像のようなGANと同等の非常に質の高い画像を生成することができるようになっています。

以下は1024x1024という高画質の人物画像ですが、本物と見分けがつかない非常にキレイな画像が生成されていますね。

さて、ではVQ-VAE2とVQ-VAEはどう違うかというと、VQ-VAE2はVQ-VAEに局所的な情報を持つ潜在変数(local latent variable)と大域的な情報を持つ潜在変数(global latent variable)という2つの階層的な潜在変数を導入したところが大きく違います。
そしてこの階層的な潜在変数の導入により、サイズの大きな高解像度の画像をキレイに生成することができました。
他にも工夫はあるものの、VQ-VAEとの大きな違いはここなので、VQ-VAEを理解していればVQ-VAE2も難しくありません。
では、論文に沿って見ていきましょう。
VQ-VAE2の論文はこちらです。
『Generating Diverse High-Fidelity Images with VQ-VAE-2』
目次
VQ-VAE(Vector-Quantized Variationl Auto-Encoder)のおさらい
VQ-VAEは、VAE(Variational Auto-Encoder)の派生ですが、VAEの潜在変数が正規分布に従う連続的な変数だったのに対し、VQ-VAEの潜在変数は離散的なベクトルになります。
全体像は以下の図の通りで、潜在変数\({\bf{z}}\)を\({\bf{e}}_1, {\bf{e}}_2, \cdots\)という\(K\)個の離散的なベクトルを使って表します。
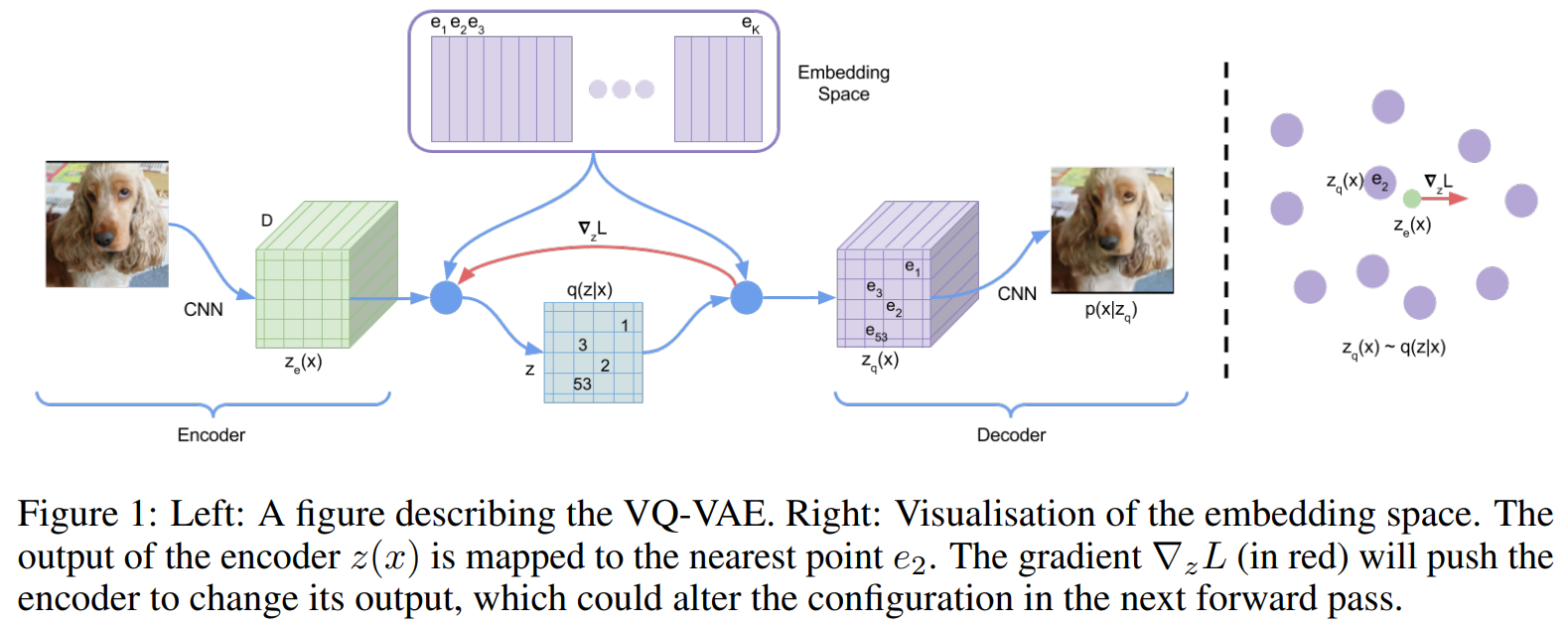
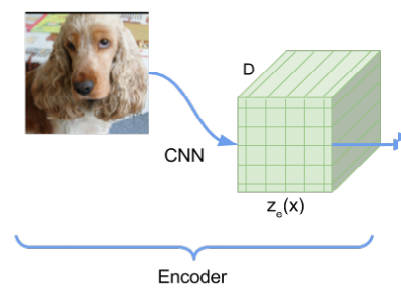
例えば、256x256(x3RGBチャネル)の画像をインプットとすると、それをCNNで処理(エンコード)します。
そのエンコードした結果が32x32だとすると、その1つ1つの位置はD次元のベクトルになっています。
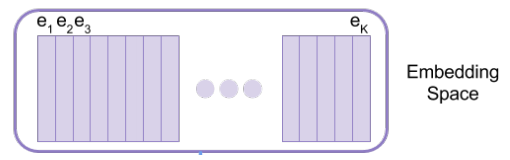
そして、以下のコードブック(codebook)と呼ばれるK個のベクトルの集合を見にいきます。
各エンコードされたD次元ベクトルについて、このコードブックの中から一番近いものを選びます。
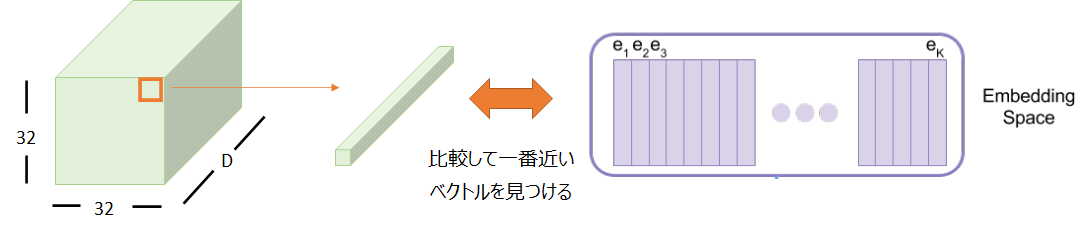
その一番近いベクトルをその位置の潜在表現として設定します。
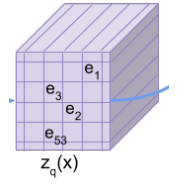
これを32x32のすべての位置について行います。
つまり、32x32の各点に対して、K個のうちの一つのベクトルが割り当てられます。これが“離散的”という意味です。
数式を使って説明
では、数式を使ってもう少し詳しく表現してみましょう。
オート・エンコーダの仕組み
インプットを\({\bf{x}}\)とするとニューラル・ネットワークでエンコードし、それを\(E({\bf{x}})\)とします。
このエンコードした\(E({\bf{x}})\)をもとに、\(K\)種類のベクトルの集まり(コードブック)から一つベクトルを選びます。
このとき、以下のように、エンコードした\(E({\bf{x}})\)に一番近いベクトル\({\bf{e}}\)を選びます。
$$\text{Quantize}\left(E({\bf{x}})\right)={\bf{e}}_k \hspace{10pt}\text{where }k=\arg\min_{j}\|E({\bf{x}})-{\bf{e}}_j\|$$
ちなみに、この\(\arg\min\)のオペレーションは微分できないので、学習時には勾配をそのまま流すstraight estimatorを使います(ここの詳細は省略しますので、VQ-VAEの記事を参照ください)。
これにより出来上がった潜在変数({\bf{z}}\)をデコーダ\(D\)で元の画像に復元します。これを\(D({\bf{e}})\)とします。
損失関数
学習時には以下の損失関数を最小化します。
$$\mathcal{L}\left({\bf{x}},D({\bf{x}})\right)=\|{\bf{x}}-D({\bf{e}})\|_2^2+\|sg\left[E({\bf{x}})\right]-{\bf{e}}\|_2^2+
\beta \|sg \left[{\bf{e}}\right]-E({\bf{x}})\|_2^2 $$
一項目を再構築誤差(reconstruction error)もしくは再構築損失(reconstruction loss)と呼びます。
再構築した画像\(D({\bf{x}})\)が元の画像\({\bf{x}}\)と近くなるようにするものです。
二項目はコードブック損失(codebook loss)と呼び、埋め込みベクトル\({\bf{e}}\)がエンコードした\(E({\bf{x}})\)に近くなるように更新するための項です。
ここで\(sg\)はstop gradientの略で、勾配は計算しません。
\({\bf{e}}\)を更新するためのものなので、\(E({\bf{x}})\)の方の勾配は計算しないということです。
三項目はコミットメント損失(commitment loss)もしくは潜在損失(latent loss)と呼び、エンコーダの出力を埋め込みベクトルに近くなるように仕向ける項です。
イメージとしては、今回はこの3番目のベクトルだったけど、今回は10番目のベクトルといった感じで、選ばれるベクトルがころころ変わりすぎないようにするための項です。
\(\beta\)はハイパーパラメータです。
指数移動平均によるコードブックの更新
埋め込みベクトルを更新する際に以下のように指数移動平均で更新するように提案されています(ちょっとややこしいので読み飛ばしていただいても良いと思います)。
$$\begin{align}
N_i^{(t)}&:=N_i^{(t-1)}*\gamma +n_i^{(t)}(1-\gamma),\\
m_i^{(t)}&:=m_i^{(t-1)}*\gamma +\sum_j^{n_i^{(t)}}E(x)_{i,j}^{(t)}(1-\gamma),\\
{\bf{e}}_i^{(t)}&:=\frac{m_i^{(t)}}{N_i^{(t)}}
\end{align}$$
\(n_i^{(t)}\)は、\(t\)番目のミニバッチにおいて、コードブック上の\(i\)番目の埋め込みベクトル\({\bf{e}}_i\)が選択されている数です。
ようはミニバッチ中で\(n_i^{(t)}\)個だけ\({\bf{e}}_i\)にマッピングされるということです。
その指数移動平均が\(N_i^{(t)}\)で、\(\gamma\)は減衰パラメータです。
同様に\(m_i^{(t)}\)は\(i\)番目の埋め込みベクトルにマッピングされるエンコードされたベクトル\(E(x)\)の合計です。
そして、\({\bf{e}}_i^{(t)}=\frac{m_i^{(t)}}{N_i^{(t)}}\)としているので、\(i\)番目の埋め込みベクトルにマッピングされるエンコードされたベクトル\(E(x)\)の指数移動平均を\(i\)番目の埋め込みベクトルに更新するということです。
これによりコードブック損失を表現し、埋め込みベクトル\({\bf{e}}\)を更新します。
潜在変数空間の学習
以上で、オート・エンコーダ部分の学習ができ、\({\bf{x}}\)を潜在変数空間にエンコードすることができました。
これだけでは画像は生成できません。
そこでVQ-VAEでは、例えば、この32x32の潜在変数空間にエンコードされたものを、PixelCNNと言った画像の生成モデルで学習します。
これがステージ2と呼ばれるものです。
これにより、学習済みPixelCNNで潜在変数を生成することができるので、そこからVQ-VAEのデコーダを使って、本来の画像を生成するという仕組みです。
PixelCNNについては以下の記事をご参照ください。
VQ-VAE2の仕組み
では、ここから本題のVQ-VAE2の仕組みについて説明します。
VQ-VAE2は基本的にはVQ-VAEと同じ考え方です。
大きく違うところは、局所的な情報と大域的な情報の両方を捉えるために、階層的なVQ-VAEを使っている点です。
ステージ1:階層的潜在コードの学習
階層的とは以下の図のような処理を行うことを言います(詳細はこれから説明します)。
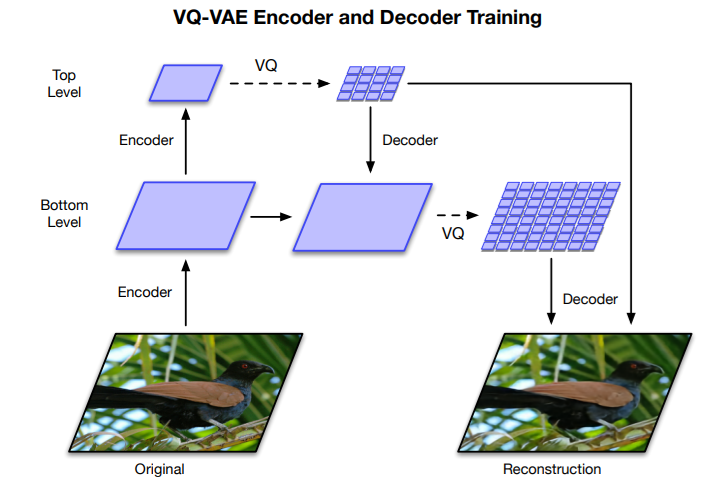
まず、元の画像をCNN(Convolutional Neural Network)でBottomレベルに圧縮し、その後Topレベルまで圧縮します。
256x256の画像だとbottomレベルでは64x64、topレベルでは32x32になります。
このBottomレベルは局所的な情報を表現していると考えられます。
そして、TopレベルはBottomレベルをさらに圧縮しているので、より大域的な情報を表現していると考えられます。
VQ-VAE2では大域的な潜在変数と局所的潜在変数という階層的な潜在変数を導入する
- Bottomレベル
局所的な情報を持つ - Topレベル
局所的な情報を持つBottomレベルの情報を集約しているので大域的な情報を持つ
そして、以下の部分のようにTopレベルのエンコード結果を離散的なベクトルで表現します。
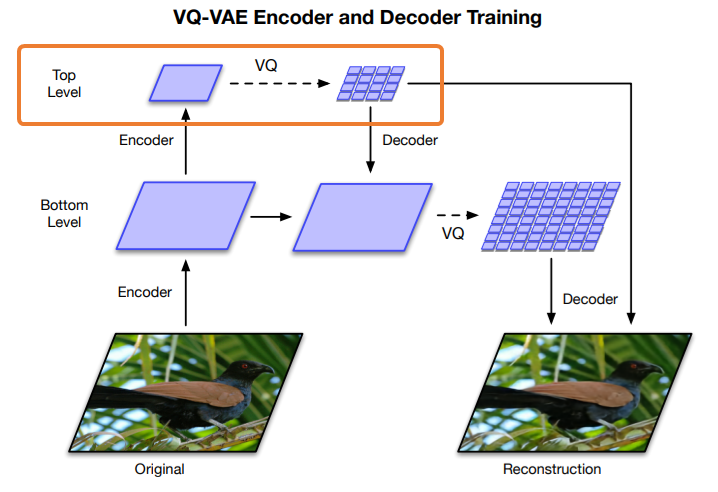
離散的なベクトルで表現というのは、VQ-VAEと同じでコードブックから一番距離が近いベクトルを取ってきて、それで表現するということです。
次に、Bottomレベルを離散的なベクトルで表現しますが、その際にTopレベルの埋め込み表現も使います。
つまり、インプットは\(E_{bottom}({\bf{x}})\)と\({\bf{e}}_{top}\)を結合したものになります。
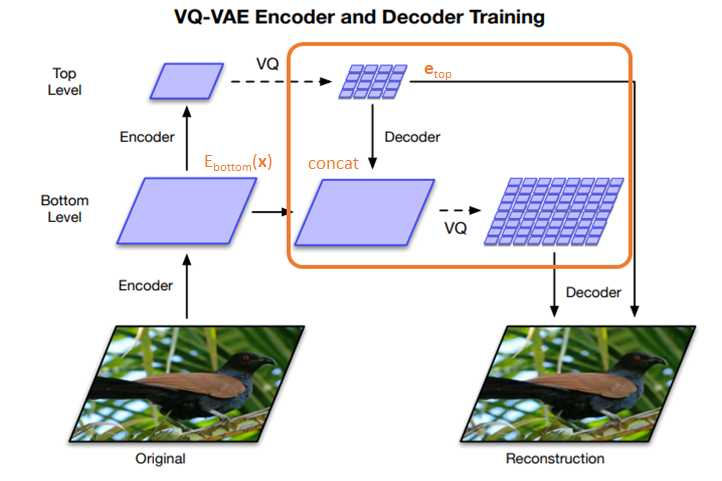
感覚的には、局所的な情報に関する潜在変数を獲得するためには、全体像を把握しておく必要がある、というようなものです。
そして、最後に\({\bf{e}}_{top}\)と\({\bf{e}}_{bottom}\)をデコーダで再構築します。
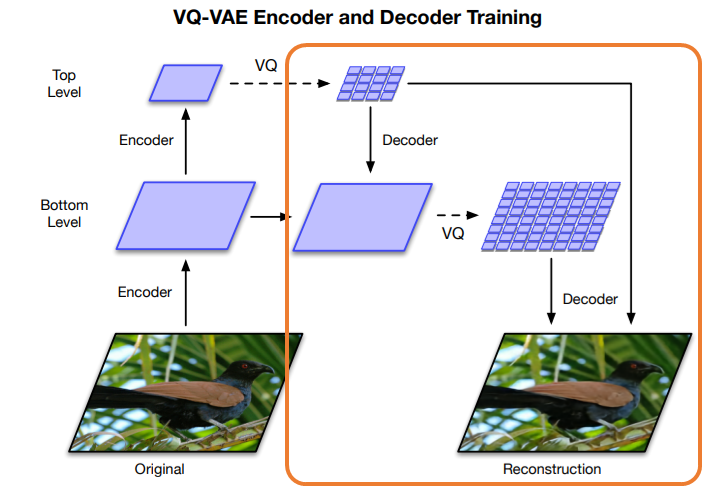
アルゴリズム
では、アルゴリズムを確認しておきましょう。
アルゴリズムは以下です。

エンコーダ
まず、1でインプット画像\({\bf{x}}\)を\({\bf{h}}_{top}\)にエンコードしています。
2で、このエンコードした\({\bf{h}}_{top}\)を、それぞれの位置について以下の式でコードブックから対応する埋め込みベクトルを設定します。
$$\text{Quantize}\left(E({\bf{x}})\right)={\bf{e}}_k \hspace{10pt}\text{where }k=\arg\min_{j}\|E({\bf{x}})-{\bf{e}}_j\|$$
そして、次からBottomです。
3の通り、Bottomレベルでは、インプット画像\({\bf{x}}\)とTopレベルの潜在変数である\({\bf{e}}_{top}\)を連結して、その連結したインプットを\({\bf{h}}_{bottom}\)にエンコードしています。
このTopレベルの求めた潜在変数もインプットにするところがポイントですね。
そして、4で\({\bf{e}}_{bottom}\)に最終的な離散ベクトルにエンコードします。
ここまでがエンコーダ部分です。
デコーダ
次にデコーダ部分ですが、こちらはTopレベルとBottomレベルの潜在変数\({\bf{e}}_{top}\)、\({\bf{e}}_{bottom}\)をインプットとして、ニューラルネットワークでインプットを再構築します。
パラメータの更新
そして、以下の損失関数により損失を計算し、6の通りパラメータをアップデートします。
$$\mathcal{L}\left({\bf{x}},D({\bf{x}})\right)=\|{\bf{x}}-D({\bf{e}})\|_2^2+\|sg\left[E({\bf{x}})\right]-{\bf{e}}\|+
\beta \|sg \left[{\bf{e}}\right]-E({\bf{x}})\| $$
ステージ2:潜在コード上の事前分布の学習
VQ-VAEではPixelCNNを使って、潜在変数の分布を学習していました。
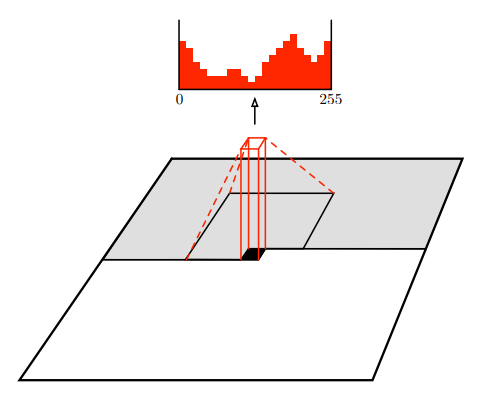
潜在変数の分布を学習するというのは、画像から生成された離散的な潜在変数(オレンジの矢印)の分布を別のモデルで学習するということです。
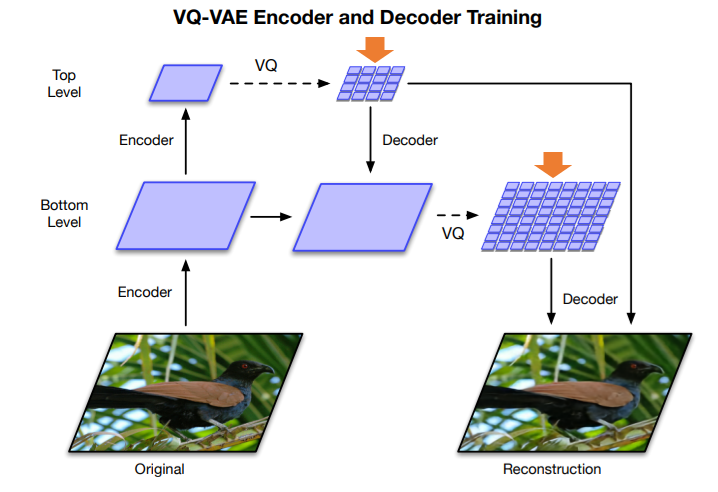
以下の図のように、画像そのものを学習するのではなく、潜在変数を学習することになります。
PixelCNN Decoders』
https://arxiv.org/abs/1606.05328
ここで、VQ-VAEの場合は1つのモデルでしたが、VQ-VAE2の場合はTopレベルの潜在変数とBottomレベルの潜在変数があるので、2つのモデルを学習することになります。
また、VQ-VAE2ではPixelCNNにself-attentionの仕組みを取り入れたPixelSnailを参考にself-attentionの仕組みを導入します。
Topレベルの潜在変数は32x32のサイズでattentionを使ったPixelCNNを使って学習し、self-attentionを使います。
一方で、局所的な情報のみを含んでいるBottomレベルの方は、attentionを使うメリットが小さいことと、64x64とサイズが大きいのでメモリ負荷が大きいため、self-attentionは使いません。
アルゴリズム
では、ステージ2のアルゴリズムを見ていきましょう。

潜在変数の作成(1-7行目)
Stage2では潜在変数の分布を学習するので、まず、2-6で学習のためのデータを作成します。
3行目、4行目ではStage 1のときと同じ方法で、それぞれTopレベルとBottomレベルの潜在変数を求めます。
繰り返しになりますがBottomレベルの潜在変数を計算する際にはTopレベルの潜在変数もインプットとしています。
そして、得られた潜在変数をそれぞれ\({\bf{T}}_{top}\)と\({\bf{T}}_{bottom}\)に入れていきます。
潜在変数の分布の学習(8, 9行目)
8でTopレベルの潜在変数\({\bf{T}}_{top}\)をインプットとして、\(p_{top}\)というself-attention付きのPixelCNNモデル学習します。
9では、Bottomレベルの潜在変数\({\bf{T}}_{bottom}\)とTopレベルの潜在変数\({\bf{T}}_{Top}\)をインプットとすることにより、Topレベルの潜在変数で条件付けしたBottomレベルの潜在変数の分布を\(p_{bottom}\)というモデルで学習します。
これで潜在変数の生成モデルができました。
サンプルの生成(10-14行目)
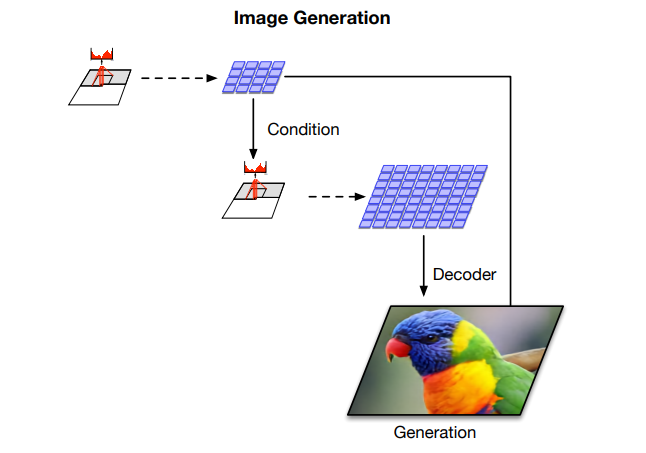
まず、11でTopレベルのモデル\(p_{top}\)を使って、潜在変数\({\bf{e}}_{top}\)を生成します。
次に、12で、Bottomレベルのモデル\(p_{bottom}\)を使って、潜在変数\({\bf{e}}_{bottom}\)を生成します。
この際に\({\bf{e}}_{top}\)を条件として与えてやります。
そして、最後に13で\({\bf{e}}_{top}\)、\({\bf{e}}_{bottom}\)をステージ
1で学習済みのVQ-VAEのデコーダにインプットすることで画像を生成します。
使うのはデコーダのみです。
図で表すと以下のようになります。
Rejection Sampling
今までの手法を使うと画像を生成することができますが、例えば左上と右下で一貫していないというようなサンプルが生成される場合もあります。
そこで、VQ-VAE2では、事前にImageNetを使って学習したモデルを使って、想定したクラスに正しく分類されたサンプルのみを出力するという仕組みを導入します。
つまり、猫なら猫の画像に見えると別モデルで判断される画像のみを出力するというものです。
ですので、quality(質)とdiversity(多様性)の観点では、diversityは下がりますが、その分qualityを上げようとしています。
実験
では、ここから実際に生成した画像で精度を比較・確認します。
まずは、生成された画像を見てみましょう。
上から、イソギンチャク(?)、サンゴ、ナメクジ、…となっています。
何となく、まだ生成された画像かな?とわかりそうなものもありますが、まったくわからないものもありますね。

次に、BigGANとの比較です。
右がBigGAN-Deepで左がVQ-VAE2により生成された画像です。

quality(質)は同程度とのことで、diversity(多様性)は左のVQ-VAE2の方が優れているのがわかりますね。
近年ではだいぶ改善されているようですが、やはりGANは似たような画像を出力してしまう傾向があるようですね。
個人的にはVQ-VAE2は若干ボケているようにも見えなくはないで、qualityに関してはGANが上回っているかなと感じます。
高解像度データ
続いて、FFHQデータセットを使った実験です。
FFHQデータセットは1024x1024という高解像度の画像70,000枚からなるデータセットです。
高解像度なので、きちんと長期の依存関係という大域的な情報を捉えていないと、右と左で目の色が違う、口は笑っているけど目は笑っていない、などといったことが起こっています。
以下がVQ-VAE2で生成した画像です。

目の色や表情を見ても、長期のを捉えられていることがわかります。
評価指標を使って比較
今までは目で見て評価していましたが、ここからは評価指標を使って確認していきます。
FID、IS、Precision-Recall
BigGANと比較します。
FIDやIS、Precision-Recallについてはこちらの解説がわかりやすいので、ご参照ください。
GAN — How to measure GAN performance?
右図のPrecision-Recallの結果を見てみましょう。
Precisionはquality(質)、Recallはdiversity(多様性)を表していると考えられます。
Recallは明らかにVQ-VAEがBigGANを上回っており、Precisionは若干BigGANを下回っています。
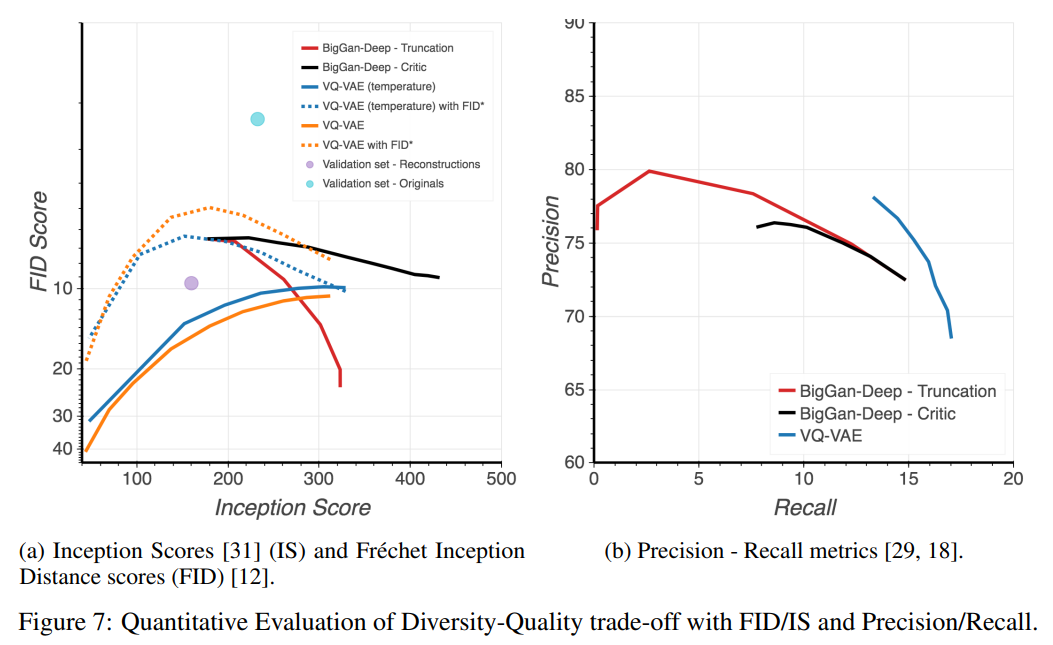
このことから、quality(質)は若干BigGANが優れており、diversity(多様性)はVQ-VAE2が優れていると考えられます。
ただし、あくまで評価指標による評価なので、それには欠点があることに留意が必要です。
Classification Accuracy Score(CAS)
Classification Accuracy Score(CAS)は以下の論文で提案された生成モデルの評価指標です。
『Classification Accuracy Score for Conditional Generative Models』
CASを使った場合の結果は以下です。

Top-1 accuracy、Top-5 accuracyともにVQ-VAE2がBigGANを上回っているようですね。
まとめ
今回は、VQ-VAEを進化させたVQ-VAE2を見てきました。
VQ-VAEの仕組みからそれほど大きくは変わりませんが、階層的な潜在変数を導入することにより、局所的な情報と大域的な情報を捉えることができ、高解像度でもうまく生成されるようになりました。
GANと比較すると、私の解釈では、精度は若干GANの方が上、多様性はVQ-VAEの方が若干上もしくは同程度、スピードはVQ-VAEの方が速い、という認識です。
特にVQ-VAEはGANと比べて非常に軽いので、個人でも学習しやすいのがいいですね。
では、また次回にお会いしましょう!

