Gumbel-Max Trick(ガンベル最大トリック)を理解する

さて、今回はカテゴリカル分布から効率的にサンプリングする方法であるGumbel-Max Trick(ガンベル最大トリック)について解説したいと思います。

Gumbel-Max Trickを使うと、Deep Learningなどでよくあるようにsoftmax関数を通して確率を計算することなく、logitから直接効率的にサンプリングすることが可能です。

Gumbel-Max Trickを使ってGumbel-Softmaxに繋がり、離散的な潜在表現を持つモデルのバック・プロパゲーションが可能になります。

では、早速見ていきましょう。

Gumbel-Max Trick(ガンベル最大トリック)とは

Gumbel-Max Trickはカテゴリカル分布からsoftmax関数を通す前のlogitを使って、並列計算により効率的にサンプリングする方法です。

まず、カテゴリカル分布から普通にサンプリングする場合を説明します。

カテゴリは1~5の5つとし、それぞれのカテゴリのlogit \(u\)を0.1, 0.2, 0.4, 0.1, 0.2とします。

u = np.array([1.2, 2.3, 1.4, 3.3, 0.1])

つまり、各カテゴリを取る確率はsoftmax関数で計算することができます。

$$\text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}$$

softmax関数で確率にすると0.07, 0.22, 0.09, 0.60, 0.02という感じです。

本来softmax関数はオーバーフローを意識して実装しないといけませんが、Gumbel-Max Trickはロジットから直接計算することができるので、オーバーフロー意識しなくてよいという利点もあります。

そして、以下の手順でサンプリングすることができます。

1. 1~5の整数(カテゴリ数)を取る一様乱数を振り、出た数値のカテゴリを候補とします。
2. 0~1の一様乱数を振り、それが1で選んだカテゴリの確率以下であればそのカテゴリをサンプリングします。
3. そのカテゴリの確率より大きければ、はじめに戻ります。

という方法で可能です。

では、まずは、実際に通常の方法でサンプリングしてみましょう。

100,000個のサンプルを取得します。

import numpy as np

num_of_samples = 100000

まず、サンプリングします。

counter, counter_total = 0, 0
samples = []
while 1:
  counter_total += 1

  cat_rnd = np.random.randint(1, len(pi)+1) # カテゴリを選択
  cat_prob = pi[cat_rnd - 1] # カテゴリを取る確率
  gen_rand = np.random.uniform() # 一様乱数を振る
  if gen_rand < cat_prob: # 乱数がカテゴリを取る確率より小さければ採択。大きければもう一度やり直す。
    samples.append(cat_rnd)
    counter += 1
  if counter >= num_of_samples:
    break

確率を計算します。

arr_prob_of_samples = np.zeros(len(pi))
for i in samples:
  arr_prob_of_samples[i-1] += 1
arr_prob_of_samples /= arr_prob_of_samples.sum()  

では、表示してみましょう。Plotlyを使っていますが、インタラクティブにする必要はありません(Plotlyの使い方については、こちらの記事をご参照ください)。

import plotly.graph_objects as go

trace_1 = go.Bar(x=np.arange(len(pi))+1,
                 y=pi,
                 width=0.3,
                 name='実際の確率')
trace_2 = go.Bar(x=np.arange(len(pi))+1,
                 y=arr_prob_of_samples,
                 width=0.3,
                 name='サンプリング')
layout = go.Layout(xaxis={'title': 'カテゴリ'},
                   yaxis={'title': '確率'},
                   title='通常のサンプリング')
fig = go.Figure([trace_1, trace_2], layout)
fig.show()

青が初めに設定した各カテゴリを取る確率で、赤がサンプリングによる確率です。

正しくサンプリングできていますね。

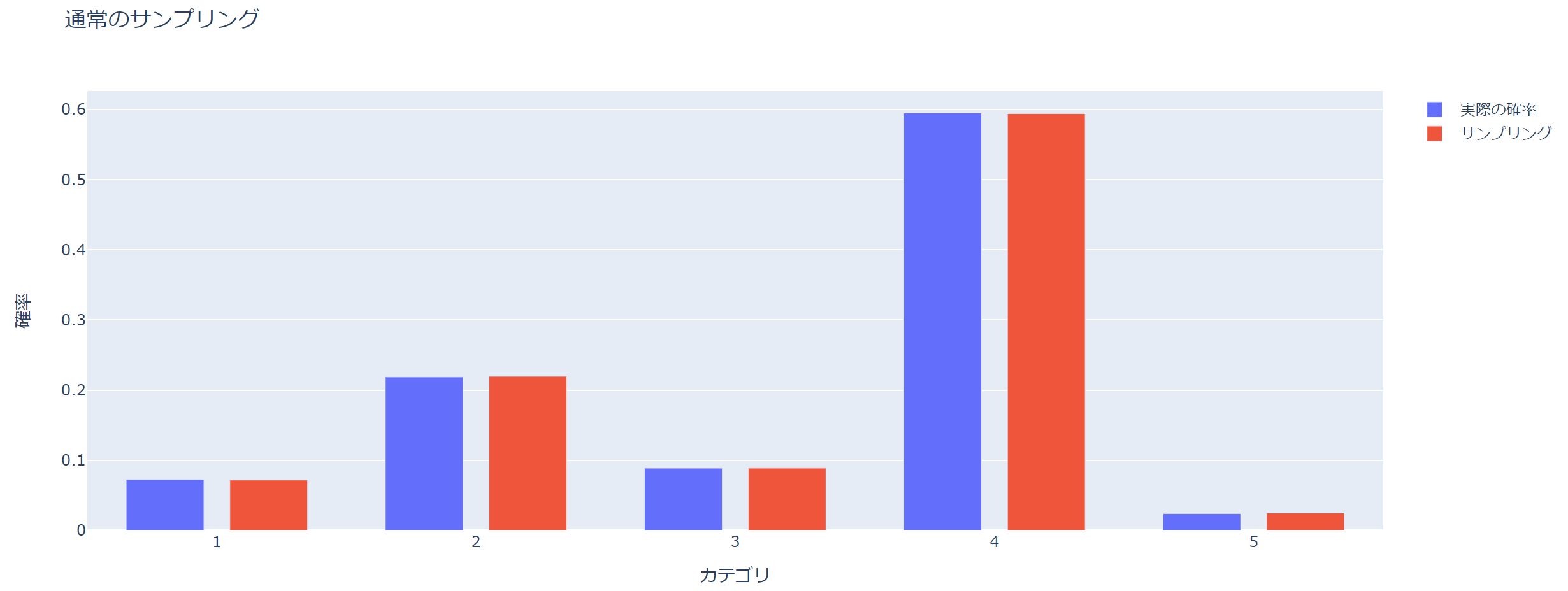
ただし、このサンプリング方法では、棄却されればやり直しになるため、100,000個のサンプルを生成するために今回だと500,000回ぐらいの試行が必要になります。

Gumbel-Max Trickを使えばそのようなことは必要ありません。

では、続いてGumbel-Max Trickについて説明していきます。

Gumbel-Max Trickのアルゴリズム

位置パラメータが0、尺度パラメータが1のGumbel分布は、以下のような分布関数\(F(x)\)と密度関数\(f(x)\)を持つ確率分布になります。

そして、logitを\(u_i\)とします。

このとき、各カテゴリを取る確率は、softmax関数を使って

$$\begin{align}
p_i = \frac{\exp(u_i)}{\sum_j \exp(u_j)}, \hspace{10pt} i=1,\cdots, K
\end{align}$$

で表されます。

ここで、Gumbel分布からの乱数を\(G_i\)として、

$$
Z_i = u_i +G_i
$$

を定義します。

するとこのとき、\(Z_k\)が\(i\neq k\)の中で最大値を取る確率は、\(p_k\)と一致します。

つまり、\(Z_k\)が最大のインデックスを取る確率が\(p_k\)なので、Z_iをサンプリングして、最大のインデックスとなったカテゴリを選ぶことで、\(p_i\)からサンプリングすることが可能という仕組みです。

この証明はあとでしますので、まずは実際にこれでうまくサンプリングできるかを見ていきましょう。

サンプリング

では、実際に実装してみましょう。

Gumbel分布に従う乱数は、一様乱数を振って、それをGumbel分布の逆関数に入れることにより発生させます(逆関数法)。

Gumbel分布は以下で表されるので、

$$F(x)=\exp\left(-\exp(x)\right)$$

逆関数は、

$$\begin{align}
y&=\exp\left(-\exp(-x)\right)\\
\end{align}$$

から、

$$F^{-1}(x)=\log\left(\log(x)\right)$$

となります。

ではサンプリングしてみましょう。

gumbel_max = []

for i in range(num_of_samples):
  rnd = np.random.uniform(size=len(pi)) # 一様乱数を振る
  z = u + gumbel_inverse(rnd) # 逆関数でGumbel分布に従う乱数に変換し、ロジットに足す u_i + G_i
  gumbel_max.append(np.argmax(z)+1) # zが最大となるインデックスが抽出したいサンプル

これだけでサンプリングができます。

ここにはif文がありませんので、サンプリングしたけど棄却されてもう一度、ということはありません。

実際に正しくサンプリングできているか確認しましょう。

### softmax関数
def softmax(x):
  return np.exp(x) / np.exp(x).sum()

### 確率を計算
gumbel_arr_prob_of_samples = np.zeros(len(pi))
for i in gumbel_max:
  gumbel_arr_prob_of_samples[i-1] += 1
gumbel_arr_prob_of_samples /= gumbel_arr_prob_of_samples.sum()  

# 描画
trace_1 = go.Bar(x=np.arange(len(u))+1,
                 y=softmax(u),
                 width=0.3,
                 name='実際の確率')
trace_2 = go.Bar(x=np.arange(len(u))+1,
                 y=gumbel_arr_prob_of_samples,
                 width=0.3,
                 name='Gumbel-Max Trickによるサンプリング')
layout = go.Layout(xaxis={'title': 'カテゴリ'},
                   yaxis={'title': '確率'},
                   title='Gumbel-Max Trickによるサンプリング')
fig = go.Figure([trace_1, trace_2], layout)
fig.show()

青が設定したロジットに対応する確率で、赤がGumbel-Max Trickによりサンプリングした場合の各カテゴリを取る確率です。

うまくサンプリングできていますね。

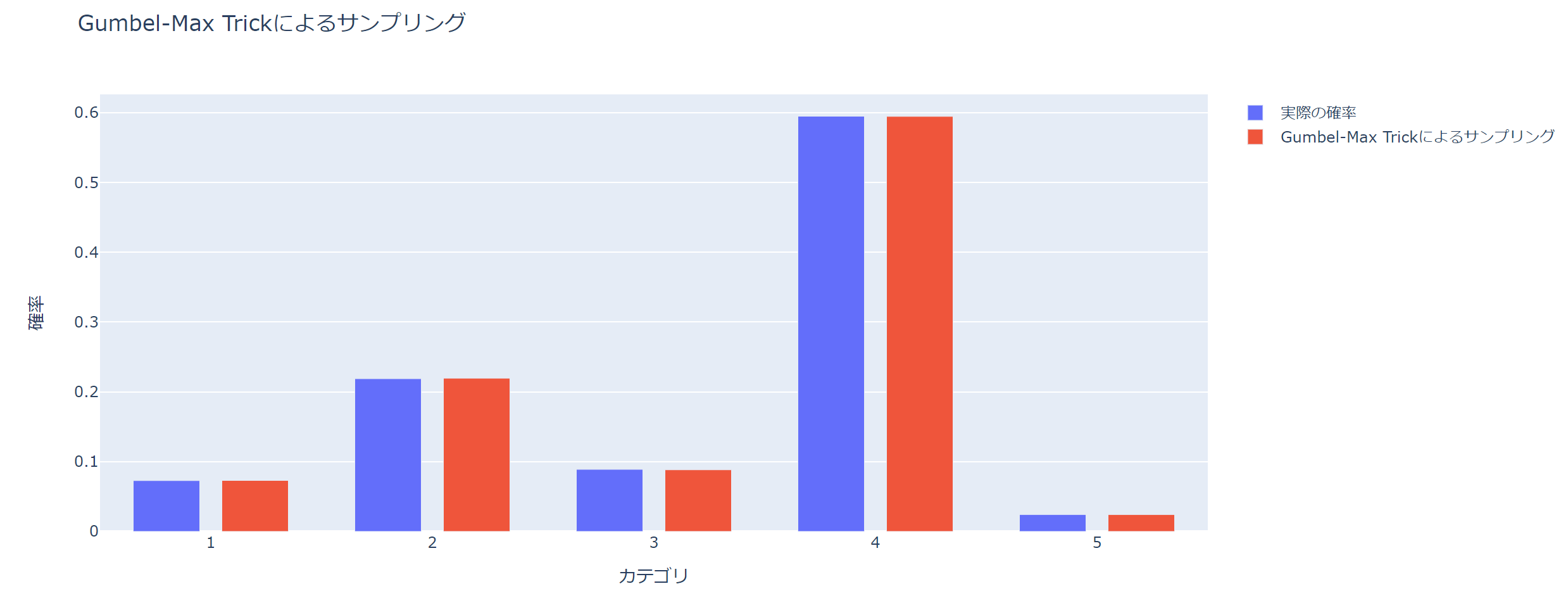
ということで、Gumbel-Max Trickでは非常にシンプルに実装することができ、サンプリングしたものの棄却されるということがなく、非常に効率的にサンプリングすることが可能です。

もちろん、並列計算によりもっと高速な実装をすることも簡単です。

つづいて、「\(Z_i\)が\(k\neq i\)の中で最大値を取る確率は\(p_i\)と一致する」というGumbel-Max Trickの最大のポイントですので、この証明を確認しておきましょう。

証明

証明したいのは、\(Z_k\)が最大になる確率、つまり\(k\)以外のインデックスに対する\(Z_i\)よりも大きくなる確率が\(P_k\)になることなので、

$$P(\forall i\neq k, Z_i<Z_k)=P_k$$

です。

まずは、\(G_k=g_k\)と固定します。

そして、ある一つの添え字\(i\)に対して、\(P(Z_i<Z_k|G_k=g_k)\)を求めます。

\(Z_i=u_i+G_i\)なので、

$$\begin{align}
P(Z_i<Z_k|G_k=g_k)&=P(u_i+G_i<u_k+g_k)\\
&=P(G_i<u_k+g_k - u_i)
\end{align}$$

となります。

したがって、Gumbel分布の分布関数を\(F(x)\)とすると、

$$\begin{align}
P(Z_i<Z_k|G_k=g_k)&=P(G_i<u_k+g_k - u_i)\\
&=F(u_k+g_k-u_i)\\
&=\exp\left(-\exp(u_i-u_k-g_k)\right)
\end{align}$$

と表されます。

ここまでは、特定の\(i\)について見てきましたが、すべての\(i\neq k\)について考えると、

$$\begin{align}
P(\forall i\neq k, Z_i<Z_k|G_k=g_k)&=\prod_{i\neq k}\exp\left(-\exp(u_i-u_k-g_k)\right)
\end{align}$$

となります。

そして、\(G_k=g_k\)という条件を取り除くために、以下のように同時分布を求め、

$$\begin{align}
P(\forall i\neq k, Z_i<Z_k, G_k=g_k)=P(\forall i\neq k, Z_i<Z_k|G_k=g_k)P(G_k=g_k)
\end{align}$$

その次に、\(g_k\)で積分することにより、求めたい確率を計算します。

$$
P(\forall i\neq k, Z_i<Z_k)=\int^{+\infty}_{-\infty} P(\forall i\neq k, Z_i<Z_k, G_k=g_k)dg_k
$$

では、計算していきましょう。

まず同時分布については、\(P(G_k=g_k)\)はGumbel分布の密度関数で、\(f(g_k)=\exp(g_k)F(g_k)\)であることから、

$$\begin{align}
P(\forall i\neq k, Z_i<Z_k, G_k=g_k)&=P(\forall i\neq k, Z_i<Z_k|G_k=g_k)P(G_k=g_k)\\
&=\prod_{i\neq k}\exp\left(-\exp(u_i-u_k-g_k)\right)\exp(-g_k)\exp\left(-\exp(-g_k)\right)\\
&=\exp(-g_k)\exp\left(-\sum_{i} \exp(u_i-u_k-g_k) \right)
\end{align}$$

と表されます。

最後の行は、\(i=k\)のとき\(u_i-u_k-g_k=-g_k\)となることを使っています。

そして、これを\(g_k\)で積分すると、

$$\begin{align}
P(\forall i\neq k, Z_i<Z_k)&=\int^{+\infty}_{-\infty}\exp(-g_k)\exp\left(-\sum_{i} \exp(u_i-u_k-g_k) \right)dg_k\\
&=\int^{+\infty}_{-\infty}\exp(-g_k)\exp\left(-\frac{\sum_{i}\exp(u_i)}{\exp(u_k)}\exp(-g_k) \right)dg_k\\
&=\int^{+\infty}_{-\infty}\exp\left(-g_k - \frac{-\exp(-g_k)}{P_k}\right)dg_k\\
&=\left[P_k \exp\left(\frac{-\exp(-g_k)}{P_k}\right)\right]^{+\infty}_{-\infty}\\
&=P_k
\end{align}$$

と求まります。

見事ですね。

計算が面倒臭いですが、一つ一つは難しくないので一度確認していただければと思います。

参考書籍

今回の証明は以下の書籍を参考にしました。

ニューラルネットワークの基礎、再帰的ニューラルネットワークなどをしっかりと理解したい方にはオススメです。

この記事で解説したGumbel-Max Trickやビームサーチに関する記述もあります。

まとめ

今回はGumbel-Max Trickを見てきました。

カテゴリ分布から効率よくサンプリングする手法で、logitから直接計算することができ、並列計算によって高速にサンプリングすることが可能です。

ここから、Gumbel-Softmaxに繋がっていきますので、次回はGumbel-Softmaxについて見ていきたいと思います。

それにしても、どうやってこれを思いついたのかが気になりますね。

では！！