今回はBERTを超えたというXLNetの論文を見ていきたいと思います。
BERTでは事前学習に“Masked LM”による双方向TransformerおよびNext Sentence Predictionという仕組みを導入し、大成功を収めました。
しかしながら、XLNetの論文ではMasked LMに関して2つの問題点が挙げられています。
Masked LMでは、文章中の15%の単語をマスクし、そのマスクされた単語を予測するというタスクを解いています。それがうまくいったわけですが、15%をマスクすることにより、マスクされた単語間の依存関係が無視されてしまいます。
例えば、“New York is a city.”という文章で、“[MASK] [MASK] is a city”とされたとします。その場合、“is a city”という単語列から、“New”と“York”をそれぞれ予測するように調整されます。
しかしながら、本来1つ目を“New”と予測すると2つ目は“York”である可能性は高いはずです。
BERTのMasked LMではそういったマスクされた単語間の依存関係が考慮されていません。
これが1点目です。
もう1点は、これはBERTの論文でも指摘されていまいたが、マスクを表す[MASK]という単語は事前学習にしか存在せず、ファインチューニング時には出現しないということです。
そこで、 BERTの双方向Transformerという良い仕組みを残しながら、Masked LM(言語モデル)を使わずに、今まで使われていたAutoreguressiveな言語モデルを使って事前学習をすることで、精度向上を図ったのがXLNetです。
BERTの詳細については以下の記事をご参照ください。
目次
XLNetの仕組み
XLNetの発想はシンプルです。
BERTの強力な特徴である“双方向の言語モデル”という特徴を残しながら、マスクを使った言語モデルの学習をしない方法を考えたということです(なぜ双方向が良いかはBERTの記事でXLNetの論文に記載されている例を使って説明しています)。
ですので、XLNetではBERTで採用されたMasked LMは使いません。
その代わりに、単語の順番をバラバラにして学習します。
詳細は後述しますが、本当に単語の順番をバラバラにしてしまうと当然おかしな文章になってしまいますので、元の文章の順番は変えずに、attentionを向ける先を限定して元の文章で自分より先に出てきた単語にもattentionを向けられるようにします。
そうすることによって、双方向の言語モデルを実現します。
また、XLNetでは、Transformer-XLの仕組みをうまく導入して、長い文章に対してもうまく対応できるようにしています。
Masked LMの問題点
Autoregressive(AR)言語モデルと(Denoising)Autoencoding(AE)言語モデル
では、まずBERTのMasked LMのどこが問題で、XLNetは何が違うかを定式化している部分を確認しておきましょう。
まず、いわゆるOpenAI GPTやLSTMなどの前向きに処理をしていく言語モデルは、それまでの単語列をもとに次の単語を予測していくため、Autoregressive (AR) 言語モデルと言われます。
一方でBERTは、一部分をマスクすることにより文章にノイズを与えて、そこから元の文章を予測するという形になっていることから、(Denoising)Autoencoding(AE)言語モデルと呼んでいます。
Autoregressive言語モデル
まず、AR言語モデルの目的変数は、文章の単語列を\({\bf{x}}=\left[x_1, \cdots, x_T\right]\)とすると、対数尤度になるので、
$$\max_\theta \log p_\theta\left({\bf{x}}\right) = \max_\theta \log p_\theta\left(x_1, \cdots, x_T\right) $$
となります。つまり、単語列の同時分布を計算します。
これを条件付き確率で置き換えることで(知っている人は読み飛ばしていただいても結構です)、
$$\begin{align}
\log p_\theta\left(x_1, \cdots, x_T\right) &= \log \left(p_\theta\left(x_T| x_1, \cdots, x_{T-1}\right)p_\theta\left(x_{1}, \cdots, x_{T-1}\right)\right) \\
&= \log \left(p_\theta\left(x_T| x_1, \cdots, x_{T-1}\right) p_\theta\left(x_{T-1}| x_1, \cdots, x_{T-2}\right) p_\theta\left(x_{1}, \cdots, x_{T-2}\right)\right) \\
&= \cdots \\
& = \sum^T_{t=1}\log p_\theta\left(x_t| {\bf{x}}_{<t}\right)\\
\end{align}$$
そして、最後の部分をニューラルネットワークの形で書くと、このようになります。
$$ \sum^T_{t=1}\log p_\theta\left(x_t| {\bf{x}}_{<t}\right)= \sum^T_{t=1}\log \frac{\exp\left(h_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x_t\right) \right) }{\sum_{x'} \exp\left(h_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x'_t\right) \right) }
$$
ここで、\( h_\theta\left({\bf{x}}_{1:t-1}\right) \)はTransformerなどにおける最後のレイヤーの隠れ層のベクトルです。
そして、\(e\left(x_t\right)\)は\(t\)時点の単語\(x_t\)の埋め込み表現なので、\(h_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x_t\right) \)は\(x_t\)に対応するlogitを計算していることになります。
\(h_\theta\left(({\bf{x}}_{1:t-1}\right)^T W_{emb}\)みたいなものですね。
それをsoftmax関数で確率に変換しているということです。
そして重要なのは、このAR言語モデルでは、
$$\max_\theta \log p_\theta\left(x_1, \cdots, x_T\right) =\max_\theta \sum^T_{t=1}\log \frac{\exp\left(h_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x_t\right) \right) }{\sum_{x'} \exp\left(h_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x'_t\right) \right) }$$
が厳密に成立している、つまり最大化したい目的関数と実際に最大化する関数が同じということです。
Denoising Autoencoding言語モデル
では、次にBERTによるmasked LM、つまりAE言語モデルを見てみましょう。
目的変数は、
$$\begin{align}
\max_\theta \log p_\theta(\bar{\bf{x}} |\hat{\bf{x}})
\end{align}$$
です。
そして、これを
$$\begin{align}
\log p_\theta(\bar{\bf{x}} |\hat{\bf{x}}) & \approx \sum^T_{t=1} m_t \log p_\theta\left(x_t|\hat{\bf{x}}\right) \\
&= \sum^T_{t=1}m_t \log \frac{\exp\left(H_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x_t\right) \right) }{\sum_{x'} \exp\left(H_\theta\left({\bf{x}}_{1:t-1}\right)^T e\left(x'_t\right) \right) }
\end{align} $$
として計算しています。
\(\bar{\bf{x}}\)はマスクされた部分の単語を表し、\(\hat{\bf{x}}\)はマスクされた単語を含む文章全体です。
また、\(m_t\)は\(x_t\)がマスクされた単語であれば1でそれ以外では0を取るindicator functionです。
つまりマスクされた部分のみを予測しているという意味になります。
そして、重要なのは左辺と右辺は厳密にはイコールではないことです。
なぜなら、一般的に
$$p(x_1, x_2)=p(x_1|x_2)p(x_2)$$
なので、
$$p(x_1, x_2)=p(x_1)p(x_2)$$
が成立するためには、\(x_1\)と\(x_2\)が独立でなければなりません。
上の例だと\(\bar{\bf{x}}\)が互いに独立でなければ等号は成立せず、そのため厳密には\( \log p_\theta(\bar{\bf{x}} |\hat{\bf{x}}) \)を最大化してはいません。
つまり、最大化したい目的関数と実際に最大化しているものが厳密には同じではありません。
具体例
論文の例では、“New York is a city”という文章に対して、「New」と「York」がマスクされた予測対象とします。
BERTのMasked LMでは、以下の対数尤度を最大化します。
$$\mathcal{J}_\text{BERT}=\log p(\text{New}|\text{is a city}) + \log p(\text{York}|\text{is a city}) $$
しかしながら、実際には「New」と「York」の出現確率には依存関係があり、独立ではありません。そこでXLNetでは、
$$\mathcal{J}_\text{XLNet}=\log p(\text{New}|\text{is a city}) + \log p(\text{York}|\text{New, is a city}) $$
を最大化します。つまり、「New」と「York」というマスクされた単語間の依存関係も考慮していることになります。
AR言語モデルとAE言語モデルの比較
では、ここで論文の通り、いったんAR言語モデルとAE言語モデルの比較をまとめておきます。
- Independence Assumption
上述の通り、BERTではマスクされた単語同士に独立性を仮定して、対数尤度を疑似的に最大化しています。
一方で、AR言語モデルでは厳密な等号が成立するように対数尤度を最大化しているので、AR言語モデルの方が優れている部分になります。 - Input noise
BERTでは事前学習の際に、文章の一定割合を[MASK]という単語に置き換えています。この[MASK]という単語はファインチューニング時には出てきません。
そのため、事前学習とファインチューニングの間に乖離が生じてしまいます(pretrain-finetune discrepancy)。
AR言語モデルではそういったことは生じません。
したがって、AR言語モデルの方がこの点では優れています。 - Content dependency
AR言語モデルでは、\(h_\theta\left({\bf{x}}_{1:t-1}\right)\)は、\(t\)時点までの単語しか考慮されていません。
一方でBERTの\(H_\theta({\bf{x}})\)は、双方向なので\(t\)時点より後の情報も使われています。
これはBERTの方が優れている部分になります。
上の2つはAR言語モデルの方が優れている点、最後の1つがBERTの優れている点です。
XLNetでは、AR言語モデルの良い部分とBERTの良い部分の両方を実現しようとしています。
XLNetの詳細
上記の通り、XLNetではBERTの双方向を考慮できるという部分と、AR言語モデルのよい部分の両方を実現するモデルです。
具体的にはPermutation Language Modelingということで、単語の順番を変えて学習させることにより、マスクを使わず双方向の言語モデルを学習します。
ただし、本当に単語の順番をバラバラにするわけではありません。
Permutation Language Modeling
BERTでは、
“New York is a city”
という文章であれば、
New [MASK] is a city
に置き換えて、[MASK]以降の単語の情報も使いながら、[MASK]部分を予測します。
AR言語モデルでは、その単語の予測は、それ以前の単語「New」という情報のみを使って行います。
つまり双方向にはなっていません。
これを、BERTのように双方向にすることを考えます。
XLNetでは、以下のようなイメージで、単語の順番を変えて、AR言語モデルを適用します。
New is city a [York]
この場合だと、「New」から「is」を予測、「New」「is」から「city」を予測という形で順に予測していき、最後は「New」「is」「city」「a」から「York」を予測します。
ですので、本来「York」よりも後にあった情報を使って、「York」という単語を予測することになります。これがXLNetの直感的な仕組みです。
この並べ方について、すべての順列を取ると、結局予測する単語以外のすべての情報を使うことになるので、双方向の情報をすべて使った言語モデルになるという発想です。
では、これを定式化しましょう。
まず、文章が\(T\)個の単語からなっており、それらの単語のインデックスを\([1, 2,\cdots,T]\)とし、インデックスの順列の集合を\(\mathcal{Z}\)とします。
そして、そのインデックスの1つの順列を\({\bf{z}}\in\mathcal{Z}\)とします。
また、\(z_t\)を\({\bf{z}}\)の\(t\)番目の要素、\({\bf{z}}_{<t}\)を \({\bf{z}}\)の\(t-1\)番目までの要素とします。
具体的な例を考えると、例えば、順序を1→3→4→5→2とした場合、\(z_t\)は以下のようになります。
| New | York | is | a | city | |
| \(t\) | 1 | 2 | 3 | 4 | 5 |
| \(z_t\) | 1 | 5 | 2 | 3 | 4 |
\(z_1\)が「New」、\(z_2\)が「is」ときて、\(z_5\)が「York」になります。
そして、すべての順列に対して、対数尤度の期待値を最大化するようにします。
$$\max_\theta \hspace{5pt} \mathbb{E}_{{\bf{z}}\sim \mathcal{Z}_T} \left[ \sum^T_{t=1} \log p_\theta \left(x_{z_t}| {\bf{x}}_{{\bf{z}}_t}\right) \right]$$
ただし、実際には単語の順番をバラバラにしてしまうと、言語モデルの学習にはならないので、元の単語の順番はそのままでpositional encodingも元の単語に行います。
そして、その代わり、attentionのマスクを調整することにより、参照する箇所のみを調整します。
これで、元の文章では先の単語になっていた単語を参照することができます。
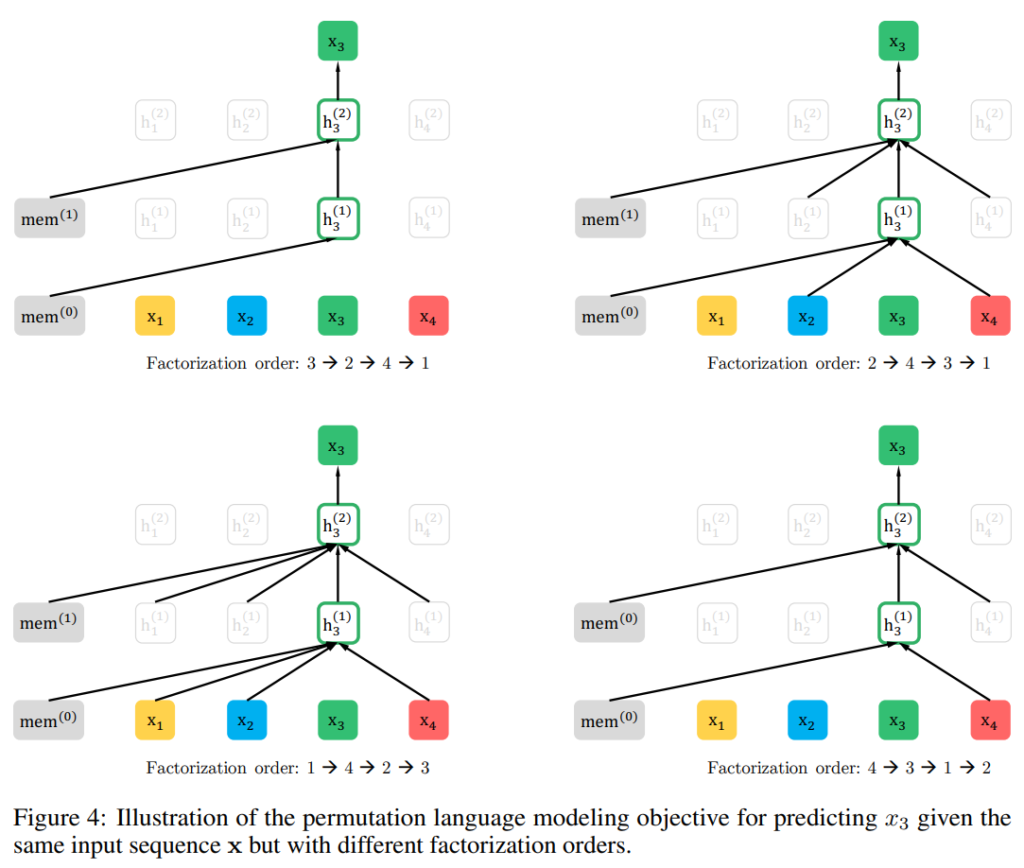
具体的な図を見てみましょう。以下の図は、\(t=3\)の隠れ層がどの時点の単語や隠れ層の値を参照するかというものです。
いくつか見てみましょう。
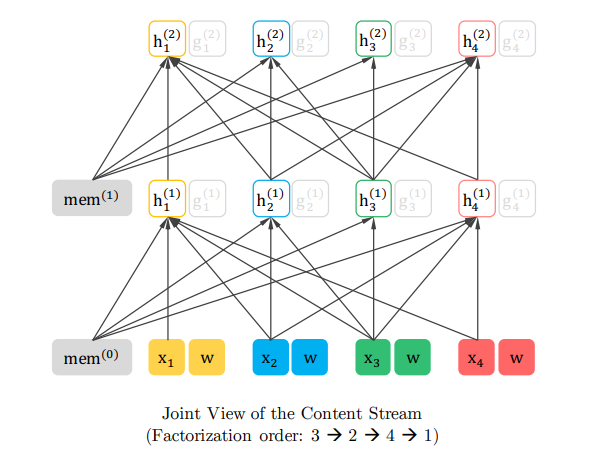
まず、以下の図は、4つの単語からなる文章があり、その単語の順番を3→2→4→1と疑似的に並び替えます。
つまり、\(z_1=3, z_2=2, z_3=4, z_4=1\)です。そして、元の文章の\(t=3\)に対応する隠れ層である\(h_3=h_{z_1}\)がどこを参照するかというと、memという“memory”部分です。
これは後述しますが、文章(パラグラフ)を複数のセグメントに分けた場合の前のセグメントの隠れ層の値を意味します。
つまり、本来、\(t=3\)の位置だと\(t=1, 2\)の単語や隠れ層の値を参照しますが、ここではしていません。
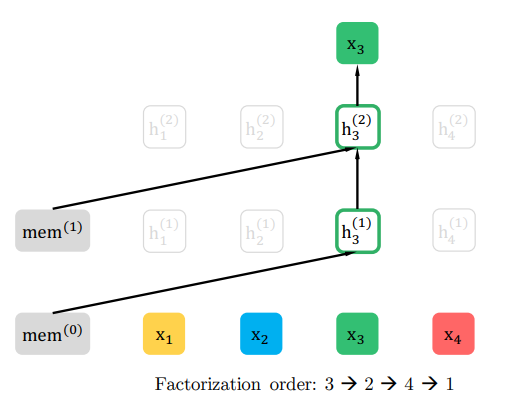
次に、単語の順番を2→4→3→1とする場合、\(z_1=2, z_4=2, z_3=3, z_4=1\)になりますが、\(t=3\)の隠れ層は、前のセグメントの隠れ層の値であるmemoryとそれより前の\(t=2\)と\(t=4\)の単語や隠れ層の値のみを参照します。
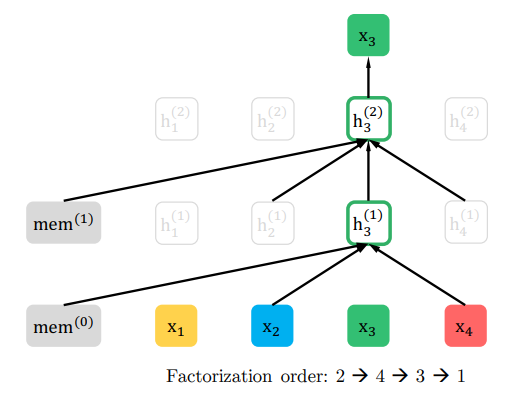
最後にもう一つだけ見ておくと、こちらは単語の順番を1→4→2→3とした場合です。
この場合は、memoryと\(t=1,2,4\)すべてを見ることができます。
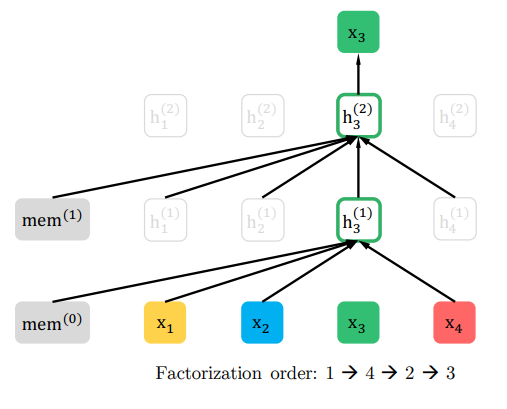
これをすべての順列で行うことにより、双方向の言語モデルと同じことを達成することができるというものです。
ただし、これをそのまま実装すると問題が出てきます。
例えば、\(z_t\)番目の単語を予測しようとすることを考えます。
その際に、使える単語は\(x_{{\bf{z}} _{<t} } \)なので、\(p_\theta\left(X_{z _t } =x|{\bf{x}}_{{\bf{z}} _{<t} }\right)\)は、Transformerの最終隠れ層のベクトル\(h_\theta\left({\bf{x}}_{{\bf{z}}_{<t}}\right)\)を使うと、
$$\begin{align}
p_\theta( X_{z_t}=x |{\bf{x}}_{\bf{z}_{<t}}) =\frac{e(x)^Th_\theta\left({\bf{x}}_{\bf{z _{<t} }}\right)}{\sum_{x'} e(x')^T h_\theta \left({\bf{x}}_{\bf{z} _{<t} }\right)}
\end{align}$$
と表されます。
\(e(x)\)は\(x\)の埋め込み表現です。
この式の右辺を見ると\({\bf{z}} _{<t} \)があるので、\(z_t\)より前の単語を参照していますが、\(z_t\)は出てきません。ですので、\(z_t\)には依存しない式になってしまい、\(z_t\)が\(i\)だろうが\(j\)だろうが、つまり\(z_1\, \cdots, z_{t-1}\)が同じであれば、元の文章の\(i\)番目の単語を予測しようとしてようが\(j\)番目の単語を予測してようが、同じ単語を予測することになってしまいます。
具体例を出すと、①②のような並べ替えを行って、[ ]内を予測するとします。
①の[ ]内はYork、②はcityですが、①②ともに「New is a」までは同じなので、次の単語を予測するときには、同じ単語を予測してしまいます。
① New is a [York] (city)
② New is a [city] (York)
このような問題が起こるのは、右辺に\(z_t\)の情報がない、つまりどの時点の単語を予測しているかという情報がないことです。
そこで、XLNetでは、以下のような式にすることで右辺に\(z_t\)の情報を付けてやります。
$$\begin{align}
p_\theta( X_{z_t}=x |{\bf{x}}_{{\bf{z}}_{<t}}) =\frac{e(x)^Tg_\theta\left({\bf{x}}_{{\bf{z}} _{<t}}, z_t\right)}{\sum_{x'} e(x')^Tg_\theta\left({\bf{x}}_{{\bf{z}} _{<t}}, z_t\right) }
\end{align}$$
\(h_\theta({\bf{x}}_{{\bf{z}}_{<t}})\)が \(g_\theta({\bf{x}}_{{\bf{z}}_{<t}}, z_t)\)になっています。
では、どうやって、これを実現するのでしょう。それがTwo-Stream Self-Attentionという仕組みです。
Two-Stream Self-Attention
では、予測する単語の場所を考慮するようにしていきます。
つまり、上式の\(g_\theta({\bf{x}}_{{\bf{z}}_t}, z_t)\)をどうするかを考えていきます。
まず、\(g_\theta({\bf{x}}_{{\bf{z}}_t}, z_t)\)の性質について考えると、\(g_\theta({\bf{x}}_{{\bf{z}}_t}, z_t)\)は\(z_t\)の情報、つまり位置情報は持っている必要がありますが、\(x_{z_t}\)自体の情報は持っていてはいけません。なぜなら\(x_{z_t}\)を予測するタスクだからです。
そこで、XLNetでは、通常のTransformerでも必要な情報\(h_\theta({\bf{x}}_{{\bf{z}}_t})\)のほかに、上記の性質を持つ\(g_\theta({\bf{x}}_{{\bf{z}}_t}, z_t)\)を同時に計算していきます。
これがTwo-Stream Self-Attentionです。
Two-Stream Self-Attentionは以下の2つの情報を流します。
- content stream
\(h_\theta({\bf{x}}_{{\bf{z}}_t})\):\(z_t\)時点までのすべての情報を含んでいる - query stream
\(g_\theta({\bf{x}}_{{\bf{z}}_t}, z_t)\):\(z_t\)より前のすべての情報と\(z_t\)時点の単語の位置情報を含んでいる
では、概念的には整理ができましたので、実際にどうやって計算するかを確認してみましょう。
content stream query streamは以下の計算により次のレイヤーの値を計算します。
$$\begin{align}
h_{z_t}^{m}&\leftarrow \text{Attention}\left( \text{Q}=h_{z_t}^{(m-1)}, \text{KV}={\bf{h}}_{z_{\le t}}^{(m-1)}; \theta \right) \hspace{5pt} \text{(content stream)} \\
g_{z_t}^{m}&\leftarrow \text{Attention}\left( \text{Q}=g_{z_t}^{(m-1)}, \text{KV}={\bf{h}}_{z_{<t}}^{(m-1)}; \theta \right) \hspace{5pt} \text{(query stream)}
\end{align}$$
\(m\)は\(m\)番目のレイヤーを表します。
まず、content stream \(h\)ですが、これは今までのSelf-Attentionと同様に、Queryが\(z_t\)における隠れ層のベクトル、Key、Valueが\(z_t\)以前の隠れ層のベクトルになります。
そして、query stream \(g\)は、Queryが\(z_t\)時点のquery streamのベクトル\(g_{z_t}^{(m-1)}\)、Key、Valueが\(z_t\)時点の単語の情報や隠れ層の情報を含まない\({\bf{h}}_{z_{<t}}^{(m-1)}\)になります。
最初のレイヤーは、\(g_i^{(0)}=w\)、\(h_i^{(0)}=e(x_i)\)(単語の埋め込み表現)を設定し、両方とも学習させるパラメータにします。
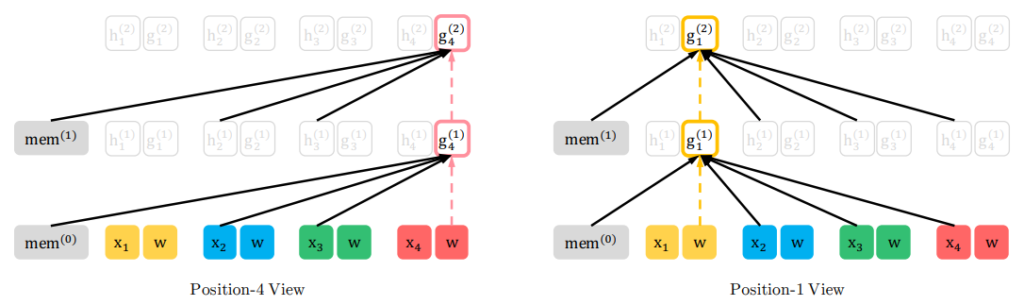
今まで説明したことを図にすると以下のようになります。
(a)のcontent streamでは\(h_1^{(1)}\)の計算のKey、Valueに\(h_1^{(0)}\)を使っているのに対し、(b)のquery streamでは、\(g_1^{(1)}\)の計算のKey、Valueに\(h_1^{(0)}\)は使っていません。
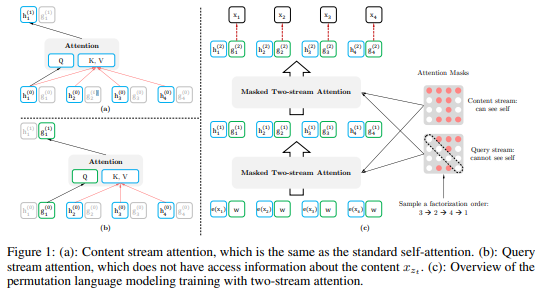
論文にはもう少し細かい図がありわかりやすいので、記載しておきます。
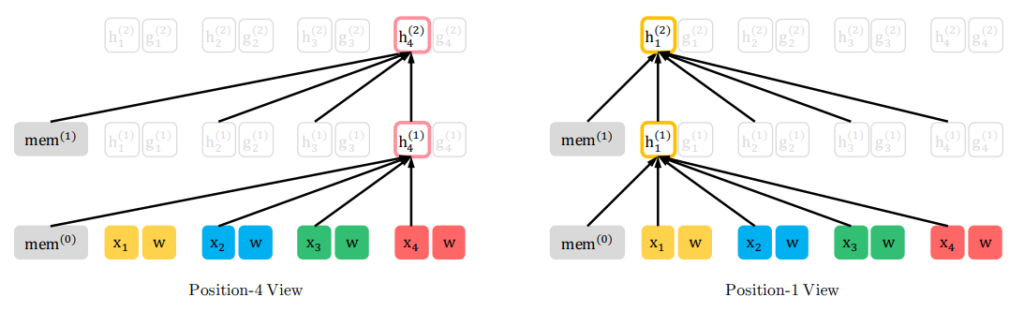
まず、content streamを見てみましょう。
content streamの全体図が以下です。順番は3→2→4→1としています。
つまり、\(z_1=3, z_2=2, z_3=4, z_4=1\) です。content streamは今までのTransformerと変わらないので、自分の位置以前および自分自身の単語や隠れ層を参照します。
\(z_1\)の位置、つまり元の文章では\(t=3\)では、memoryおよび自分自身の単語\(x_3\)と隠れ層ベクトル\(h_3\)のみにattentionを向けています。
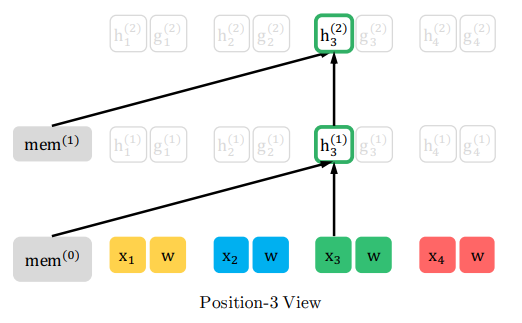
\(z_2\)の位置、つまり元の文章の\(t=2\)の位置では、memory及び、\(z_1\)の位置である元の文章の\(t=3\)の単語\(x_3\)と隠れ層ベクトル\(h_3\)と、自分自身の単語\(x_2\)と隠れ層ベクトル\(h_3\)を参照します。
\(z_3\)、\(z_4\)についても同様です。
では、次は、query streamです。こちらが全体の図になります。
query stream \(g_\theta\)では、自分自身の単語と隠れ層のベクトルは参照しません。
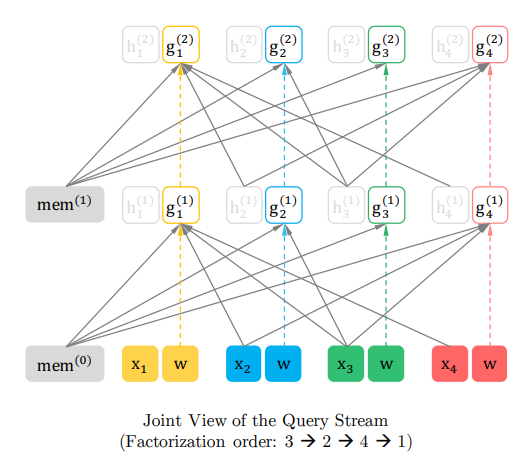
では、細かく見てみましょう。
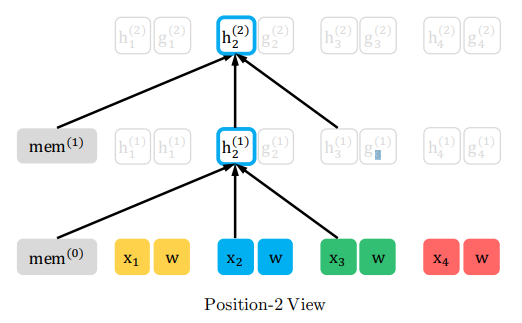
\(z_1=3\)なので、参照するのはmemoryと位置情報である\(w\)および\(g_3\)だけです。
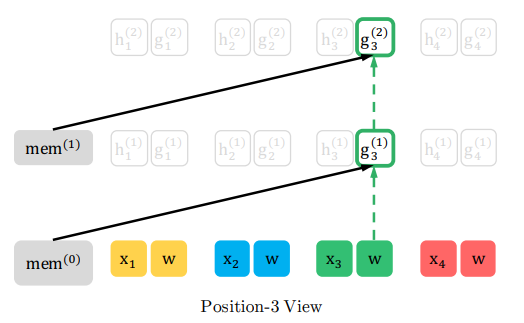
\(z_2=2\)なので、参照するのはmemoryと、\(z_1\)の単語\(x_3\)と隠れ層ベクトル\(h_3\)、そして、自分自身の時点の位置情報\(w\)と\(g_2\)です。
重要なのは\(x_2\)や\(h_2\)を見ないというところです。
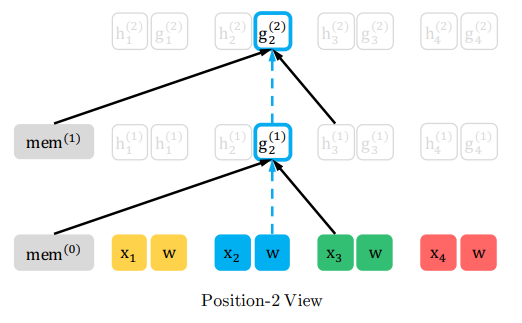
残りも同様です。
重要なのは、(並び替え後の)過去の単語や隠れ層ベクトルは参照しますが、自分自身の時点の単語や隠れ層ベクトルは見ないということです。
一応、式の方も載せておきます。
まず、初期値は、
$$h_t=e(x_t), \hspace{5pt} g_t=w$$
です。そして、context streamは、通常のTransformerの通り残差結合とLayer Normalizationを使って
$$\begin{align}
\hat{h}_{z_t}^{(m)}&=\text{LayerNorm}\left(h_{z_t}^{(m-1)}+\text{RelAttn}\left(h_{z_t}^{(m-1)},\left[\tilde{{\bf{h}}}^{(m-1)}, {\bf{h}}_{{\bf{z}}_{<t}}^{(m-1)}\right]\right)\right)\\
h_{z_t}^{(m)}&=\text{LayerNorm}\left(\hat{h}_{z_t}^{(m-1)}+\text{PosFF}\left(\hat{h}_{z_t}^{(m)}\right)\right)\\
\end{align}$$
です。Transformerについてはここでは特に詳しくは説明しません。
query streamは、
$$\begin{align}
\hat{g}_{z_t}^{(m)}&=\text{LayerNorm}\left(g_{z_t}^{(m-1)}+\text{RelAttn}\left(g_{z_t}^{(m-1)},\left[\tilde{{\bf{h}}}^{(m-1)}, {\bf{h}}_{{\bf{z}}_{<t}}^{(m-1)}\right]\right)\right)\\
g_{z_t}^{(m)}&=\text{LayerNorm}\left(\hat{g}_{z_t}^{(m-1)}+\text{PosFF}\left(\hat{g}_{z_t}^{(m)}\right)\right)\\
\end{align}$$
です。そして次の単語の予測はquery streamの最後の層\(g^{(M)}\)を使って以下で行います(Traget-aware prediction)。
$$p_\theta\left(X_{z_t}=x|{\bf{x}}_{{\bf{z}}_{<t}} \right) \frac{\exp\left(e(x)^Tg_{z_t}^{(M)}\right)}{\sum_{x'} \exp\left(e(x')^Tg_{z_t}^{(M)}\right)}$$
Partial Prediction
さて、仕組みは出来てきましたが、すべての順列に並べ替えて(実際には並び替えませんが)予測するというタスクを解くとすると、\(T\)個の文章の場合、\(T!\)個の順列を計算しないといけないので、感覚的にも大変だということはわかると思います。
そこで、partial predictionということで、すべての順列のすべての単語を予測するのではなく、バラバラにした単語列の最後の一定数の単語のみを予測するようにします。
具体的には、ある\({\bf{z}}\)という並べ替えがあったとすると、\({\bf{z}}_{\le c}\)については予測せず、\({\bf{z}}_{>c}\)だけを予測対象にします。
\(c\)の決め方ですが、ハイパーパラメータ\(K\)を導入し、\({\bf{z}}\)のうち最後の\(K\)分の1のみを予測するようにします。
論文では\(K=6\)とされているので、文章の6分の1を予測することになります。
そして、以下の対数尤度の期待値を最大化します。
$$\max_\theta \hspace{5pt} \mathbb{E}_{{\bf{z}}\sim \mathcal{Z}_T}\left[\log p_\theta\left( {\bf{x}}_{{\bf{z}}_{>c}}| {\bf{x}}_{{\bf{z}}_{\le c}} \right) \right]= \mathbb{E}_{{\bf{z}}\sim \mathcal{Z}_T}\left[\sum^{|{\bf{z}}|}_{t=c+1}\log p_\theta\left( x_{z_t}| {\bf{x}}_{{\bf{z}}_{\le c}} \right) \right] $$
Transformer-XLの導入
XLNetではTransformer-XLの以下の仕組みを導入しています。
- Recurrence Mechanism
文章もしくはパラグラフを細かいセグメントに分け、各セグメントについて再帰的に処理を行う。 - Relative Positional Encoding
絶対的な位置情報を与えるのではなく、attention計算時にqueryの単語の位置から、keyの相対的な位置情報を与える。
こちらの詳細は以下の記事をご参照ください。
まず、1つめの(Segment)recurrence mechanismですが、文章もしくはパラグラフを2つに分けるとすると、文章\({\bf{s}}\)を\(\tilde{\bf{x}}={\bf{s}}_{1:T}\)と\({\bf{x}}={\bf{s}}_{T+1:2T}\)に最初に分けます。
そして、それぞれの順列のサンプルを\(\tilde{\bf{z}}\)と\({\bf{z}}\) とします。
つまり、\(\tilde{\bf{z}}\)は\([1,\cdots, T]\)を並べ替えたもの、\({\bf{z}}\)は\([T+1,\cdots, 2T]\)を並べ替えたものになります。
そして、まずは\(\tilde{\bf{z}}\) について、上述のTwo-Stream Self-Attentionで普通に処理し、その後2つめのセグメントを処理します。2つめのセグメントを処理する際は、
$$ h_{z_t}^{m}\leftarrow \text{Attention}\left( \text{Q}=h_{z_t}^{(m-1)}, \text{KV}=\left[\tilde{{\bf{h}}}^{(m-1)}, {\bf{h}} _{z_{\le t}}^{(m-1)}\right];\theta \right) \hspace{5pt} \text{(content stream)} $$
として、前のセグメントの隠れ層のベクトル\(\tilde{\bf{h}}^{(m-1)}\)とそのセグメントの隠れ層のベクトルを連結したものをKeyとValueに設定します。
これにより、前のセグメントの情報を引き継ぐことができます。
ちなみに、Transformer-XLの記事でも説明していますが、このとき前のセグメントに関する勾配は計算しません。
Relative Positional Encodingは、文章を複数に分けることから、通常のpositional encodingではうまくいかないことに対応するものです。
単語の絶対的な位置情報を使うのではなく、attentionを向ける単語の相対的な位置情報を保持する手法です。これはTransformer-XLと同じなので、そちらを参考にしてください。
Relative Segment Encodings
BERTでは、2つの文章を事前学習の入力としますが、各文章の間に[SEP]を挟みます。
そして、一番最初の位置には[CLS]というトークンを入れますので、文章Aと文章Bの場合、[CLS], A, [SEP], Bがインプットです。
そして、A、Bをセグメントと呼び、各セグメントに対してsegment encodingということで、一方のセグメントはゼロ、もう一方には1のようにを指定して、単語の埋め込み表現に足しこみました。
これにより、どこがどのセグメント由来なのかがわかるようにしました。
XLNetでは、これについても相対的なsegment encodingとして、attentionを計算するときに考慮してやります。具体的には、\(i\)から\(j\)へのattentionを計算する際に、relative segment encodingを\({\bf{s}}_{ij}\)として、\(a_{ij}=({\bf{q}}_i + b)^T{\bf{s}}_{ij}\)をattention weightに足してやります。
ここで、\({\bf{q}}_i\)はqueryベクトル、\(b\)はheadごとのバイアス・ベクトルになります。
なお、XLNetでは2つの文章を事前学習の入力としますが、BERTで行っていたNext Sentence Preiction(NSP)は使っていません。
その理由は効果があまりなかったからとのことです(論文の実験結果をご参照ください)。
実験
設定
BERTとの比較用にBooksCorpusとEnglish Wikipediaを使って事前学習をしていますが、それに加えてGiga5、ClubWeb 2012-B、Common Crawlというデータセットも使って事前学習をしています。
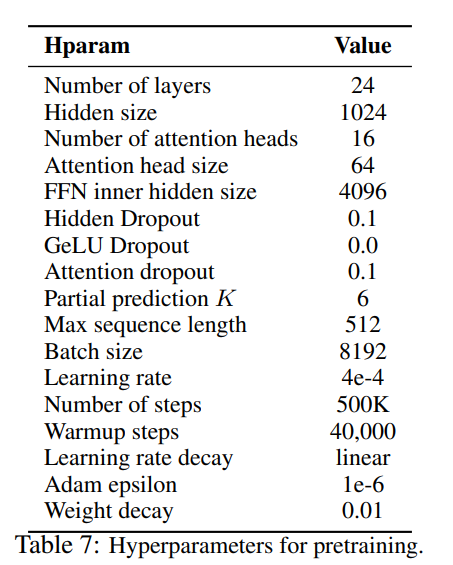
事前学習のハイパーパラメータは以下の通りです。
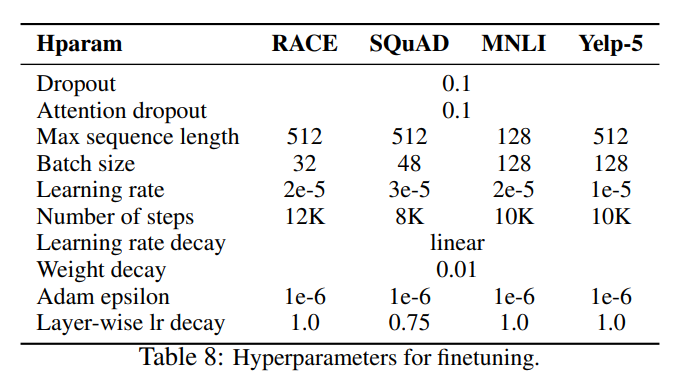
また、ファインチューニング時のハイパーパラメータはタスクごとに違い、以下の通りです。
結果
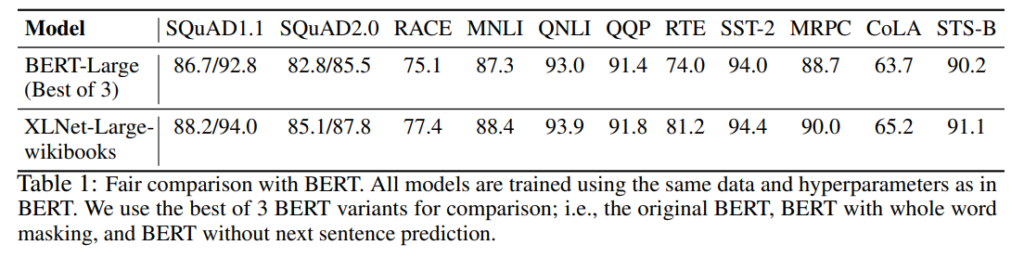
BERTとの比較
BERTと同じ事前学習データセットを使って、BERTと比較しています。タスクにより程度は異なりますが、すべてBERTを上回っています。
RoBERTaとの比較
RoBERTaは、BERTと同じアーキテクチャで、データ数を増やしたりすることにより性能向上を図ったものです。
XLNetでもデータ数を増やして事前学習して、比較しています。
RACEでは、かなり大きな差を開けて精度が改善しています。
RACEはmiddle school、high schoolの英語の試験ですが、OpenAI GPT、BERT、RoBERTa、XLNetとどんどん精度が向上していますね。
Middleでは88.6点まできています。
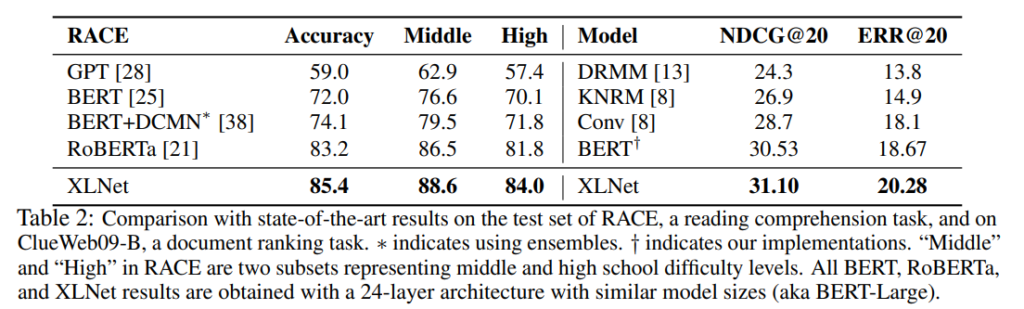
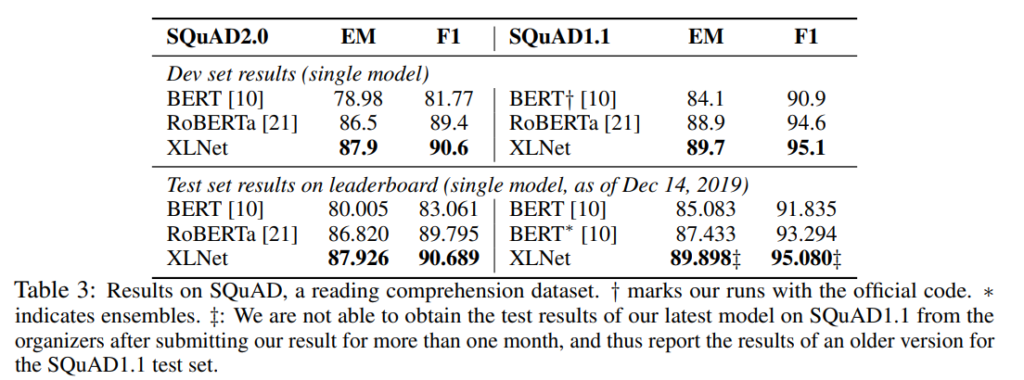
その他のデータセットでもBERTよりも大幅に精度が改善しており、RoBERTaも超えています。
論文には他のデータセットの結果もありますので、興味がある方は直接論文を参照してください。
まとめ
今回は、BERTを超えたモデルXLNetを見てきました。
個人的にはなかなか複雑な仕組みの印象です。
BERTがTransformerや事前学習の自然な拡張という感じでしたが、XLNetはかなり仕組みを工夫をして高精度を達成した感じがしますね。
いずれにせよ、RACEデータセットでどんどん精度が向上しているのが驚かされます。
では、次もまたBERTを超えたモデルの論文をご紹介したいと思います!

