以下の記事では、Diffusionモデルの仕組みについて見てきました。
もともとDiffusionモデルは画像生成モデルとして提案されましたが、その後Super Resolution用のモデルとしてSR3(Google)、テキストから画像を生成するGLIDE(OpenAI)、DALL-E2(OpenAI)などに応用され、これらのタスクのさらなる発展に寄与しています。
今回はそのDiffusionモデルをPyTorchで実装していきたいと思います。
ただ、1回では分量が多くなってしまうので、これから3回にわたって実装していきます。
以下の順番で説明していきます。
- Diffusionモデル実装編
まずDiffusionモデルの重要な仕組みであるforward process、reverse process、損失関数を実装します。 - U-Net実装編
Diffusionモデルの中のニューラル・ネットワークとして使われているU-Netを実装します。 - 学習編
1、2で作成したモデルを実際に学習していきます。
この実装にはHugging Faceのブログ『The Annotated Diffusion Model』を参考にしています。
そのままの部分がかなり多いですが、一部簡単にするため処理を省略したりしていますので、必要があればHugging Faceのブログを参照してください。
また、何度も同じ式を説明したりしていて解説がくどい部分があるかもしれませんがご容赦下さい。
では、さっそく始めましょう!
目次
Diffusionモデルとは
まず、簡単にDiffusionモデルのおさらいをしたいと思います。
詳細が気になる方は適宜こちらをご参照ください。
本サイトの解説記事 『【論文解説】Diffusion Modelを理解する』
原論文『Denoising Diffusion Probabilistic Models』
基本的な仕組み
まず、以下の図のように(1) forward processと(2) reverse processの2つの過程を考えます。
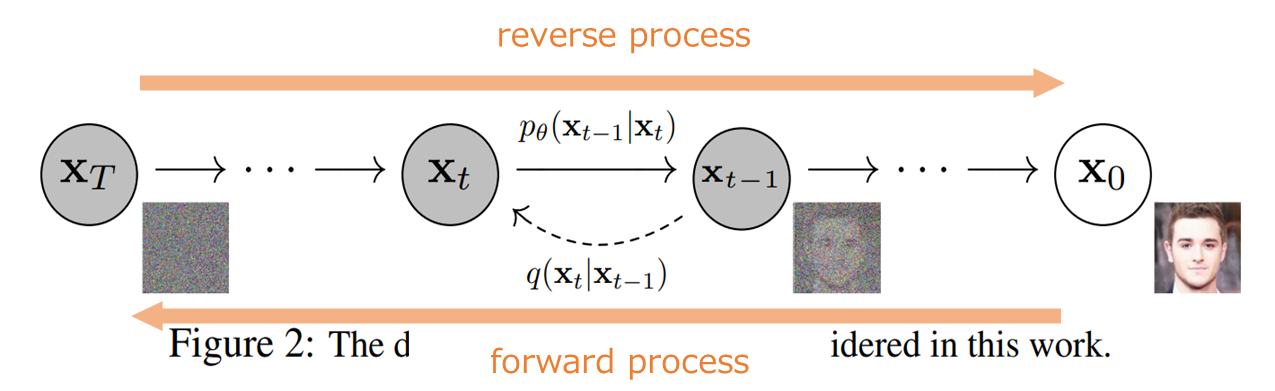
forward processは元のキレイな画像にノイズを加えていって、最終的にはノイズだけになる確率過程です。
一方のreverse processはforward processの逆で、ノイズから画像になっていく確率過程です。
そしてDiffusionモデルでやりたいことは、『画像にノイズを加えていって、最終的にノイズだけになる確率過程(fprward process)を考え、その逆をたどる(reverse process)ことでノイズから画像を生成することができる』というものです。
ですので、reverse processを学習することでノイズから画像を生成することができます。
こちらはさらにざっくりイメージです。
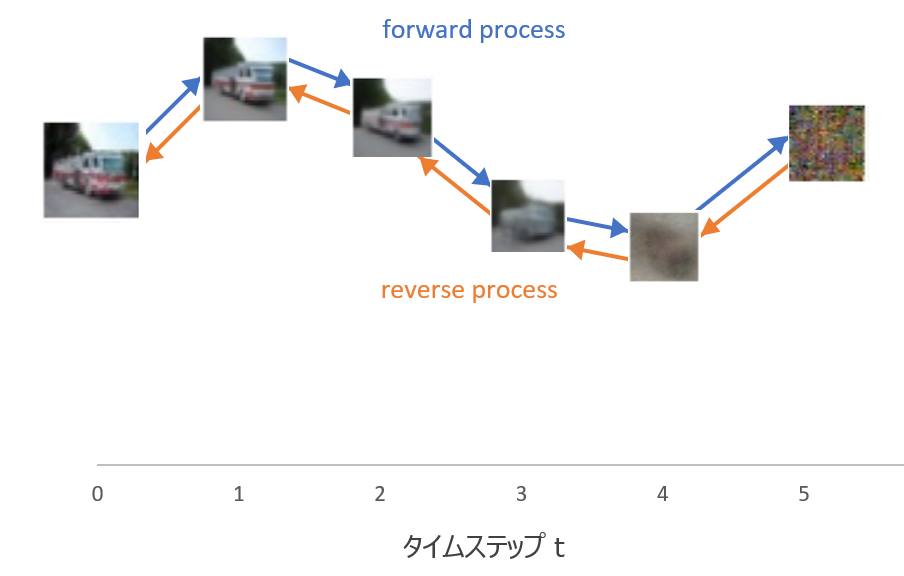
上記の図で言うと、forward processは元の画像\({\bf{x}}_0\)にノイズを加えて\({\bf{x}}_1\)、\({\bf{x}}_2\)、...となり、最終的に\({\bf{x}}_T\)というノイズだけになります。
reverse processはその逆をたどり、ノイズ\({\bf{x}}_T\)から画像\({\bf{x}}_0\)を生成します。
reverse processを学習すると、\({\bf{x}}_T\)を平均ゼロ、分散1の標準正規分布に従うノイズ(乱数)を生成し、そこから学習したreverse processで画像を生成することができます。
forward processの確率過程
では、まずforward processの確率過程を見ていきましょう。
画像にノイズを加えていくforward processは、以下の正規分布に従うマルコフ過程で定義されます。
$$\begin{align}
q_\theta({\bf{x}}_{1:T}|{\bf{x}}_{0}):&=\prod^T_{t=1}q({\bf{x}}_{t}|{\bf{x}}_{t-1}),\tag{1}\\
q({\bf{x}}_{t}|{\bf{x}}_{t-1})&=N({\bf{x}}_{t}; \sqrt{1-\beta_t }{\bf{x}}_{t-1}, \beta_t {\bf{I}}) \tag{2}
\end{align}$$
\(N\)は正規分布の分布関数を表します。
何となく難しそうに見えるかもしれませんがイメージとしては、画像\({\bf{x}}_{t-1}\)が与えられたときの画像\({\bf{x}}_{t}\)は、パラメータが\(\beta_t\)を使って表される(多変量)正規分布に従うということです。
ここで共分散はゼロとします。
(今ピンとこない方も、実際に実装しているところを見るとわかるかもしれません)
reverse prcessの確率過程
上記のforward processの分散\(\beta_t\)が小さい場合、reverse processもforward processと同じ関数形で表されることが知られています。
ですので、reverse processは以下のように定義されます。
$$\begin{align}
p_\theta({\bf{x}}_{0:T}):&=p_\theta({\bf{x}}_{T})\prod^T_{t=1}p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t}), \tag{3}\\
p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})&=N\left({\bf{x}}_{t-1}; \mu_\theta({\bf{x}}_t, t), \Sigma_\theta({\bf{x}}_t, t)\right) \tag{4}
\end{align}$$
つまり\(\beta_t\)を小さくとると、reverse processも正規分布に従うということです。
ただし、平均、分散はforward processとは異なります。
ここで出てくる\(\theta\)がニューラルネットワークのパラメータで、平均\(\mu_\theta\)・分散\(\Sigma_\theta\)をニューラルネットワークで学習するということになります。
なお、この論文では分散\(\Sigma_\theta\)は学習せず、あらかじめ固定してしまいます。
その後の論文ではタイムステップ\(t\)を減らしても学習をうまくいくようにするためには分散\(\Sigma_\theta\)も学習した方がよいという結果が出ますが、ここではいったん本論文に従い分散は決め打ちにしたいと思います。
損失関数
VAEのように変分下界を最大化することでノイズから画像を生成するreverse processのパラメータを求めるというのがDiffusionモデルです(変分下界についてはこちらの記事『【Tensorflowによる実装付き】Variational Auto-Encoder(VAE)を理解する』をご参照ください)。
ただし、上記の論文では、厳密な下界の最大化ではなく、下界の最大化から出発し様々な単純化を行うことで、以下のノイズを加えた画像からノイズを求めるという目的関数を提案しています。
$$L_\text{simple}(\theta)=\mathbb{E}_{{\bf{t}}, {\bf{x}}_0, {\bf{\epsilon}}}\left[\| \epsilon-\epsilon_\theta \left(\sqrt{\bar{\alpha}}{\bf{x}}_0
+\sqrt{1-\bar{\alpha}_t}\epsilon, t \right) \|^2\right]$$
少し補足しますと、
\begin{align}{\bf{x}}_t=\sqrt{\bar{\alpha}}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon \end{align}
が成立するので、目的関数は以下で表されます。
$$L_\text{simple}(\theta)=\mathbb{E}_{{\bf{t}}, {\bf{x}}_0, {\bf{\epsilon}}}\left[\| \epsilon-\epsilon_\theta \left({\bf{x}}_t, t \right) \|^2\right]$$
つまり、ノイズが加わった画像\({\bf{x}}_t\)と時点\(t\)という情報から、ノイズ\(\epsilon\)を予測するというニューラル・ネットワーク\(\epsilon_\theta\)を学習します。
非常にざっくりした説明ですが、とりあえず雰囲気をつかんでいただき、必要に応じて導出過程などの詳細を確認していただければと思います。
Diffusionモデルの実装
では、ここからDiffusionモデルを実装していきます。
まず、必要なモジュールをインポートしておきます。
import numpy as np from tqdm.auto import tqdm # PyTorch, 計算関係 import torch import torch.nn.functional as F # 描画用 from PIL import Image from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
補助関数
まず、配列から時点\(t\)に対応すする要素配列を取得する関数extract()を作成しておきます。
この関数は例えば\(\alpha_{0:T}\)という配列から任意の1時点\(t\)の値\(\alpha_{t}\)を抜き出す際などに使用します。
引数aという配列から引数tの時点の配列を抜き出します。
その際に、元の配列の形で返すためにx_shapeという引数を使っています。
def extract(a, t, x_shape): batch_size = t.shape[0] # バッチサイズ out = a.gather(-1, t.cpu()) # aの最後の次元 ⇒ timestepに対応するalphaを取ってくる return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device) # バッチサイズ x 1 x 1 x 1にreshape
学習フェーズ
上記で説明した通り、Diffusionモデルの学習は、元の画像にノイズを加え、そのノイズが加わった画像をインプットとして、ノイズを予測することで学習します。
元の画像にノイズを加えていくのはforward processになります。
ではforward processを実装していきましょう。
forward processの実装
forward processは、サンプルの画像からノイズだけの画像に移っていく過程で、\((1)\)式、\((2)\)式で表されました。
そして、\((1)\)式、\((2)\)式から\({\bf{x}}_0\)を与えた場合の任意の時点\(t\)の分布を求めると、以下のように表されます。
\begin{align}
q({\bf{x}}_t|{\bf{x}}_0)&=N({\bf{x}}_t; \sqrt{\bar{\alpha}_t}{\bf{x}}_0, (1-\bar{\alpha}_t){\bf{I}}) \tag{5} \\
\bar{\alpha}_t&=\prod^t_{s=1}\alpha_s \tag{6} \\
\alpha_t&=1-\beta_t \tag{7}
\end{align}
\((1)\)式だと任意の時点の\({\bf{x}}_t\)を求めるのためには逐次的に計算する必要がありましたが、\((5)\)式では1発で計算することが可能になります。
この\((5)\)式を実装していきます。
正規分布に従うので、平均と分散さえわかればサンプリングでき、平均・分散は\((5)\)式から以下で計算できます。
\begin{align}
&\text{平均 : }\sqrt{\bar{\alpha}_t}{\bf{x}}_0 \\
&\text{分散 : }(1-\bar{\alpha}_t){\bf{I}}
\end{align}
そして、\(\beta_t\) ⇒ \(\alpha_t\) ⇒ \(\bar{\alpha}_t\) ⇒ 平均・分散(標準偏差)と順に計算していきます。
ここで\(\beta_t\)の設定方法ですが、原論文では時点に対して線形に増えていくように設定されています。
def linear_beta_schedule(timesteps): beta_start = 0.0001 beta_end = 0.02 return torch.linspace(beta_start, beta_end, timesteps)
それ以外にもcos関数を使った方法も論文で提案されており、それについては、今後結果を比較したいと思います。
では、一旦線形関数で\(\beta\)が設定できたので、そこから\(\bar{\alpha}_t\)、そして平均・分散を計算するようにしていきましょう。
まず、\(\beta\)を計算します。
timesteps = 200 betas = linear_beta_schedule(timesteps=timesteps)
続いて、\(\alpha\)です。
alphas = 1. - betas
そして、\(\bar{\alpha}\)を計算します。
alphas_cumprod = torch.cumprod(alphas, axis=0)
平均・標準偏差を計算するため\(\sqrt{\bar{\alpha}_t}\)と\(1-\bar{\alpha}_t\)を計算しておきます。
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod) sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
では、最後に平均・標準偏差を計算して、時点\(t\)に対応する画像をサンプリングする関数q_sample()を作成します。
引数のx_startが\({\bf{x}}_0\)を表します。関数extract()は上で作成した\(t\)時点の値を抜き出す関数です。
def q_sample(x_start, t, noise=None):
"""
キレイな画像からノイズを加えた画像をサンプリングする.
"""
if noise is None: # 呼び出し元からノイズが渡されていなければここでで生成する.
noise = torch.randn_like(x_start) # 正規乱数
# t時点の平均計算用
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
# t時点の標準偏差計算用
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
# (5)式で計算
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
サンプリングして確認
実際に元の画像からノイズになっていく様子を確認してみましょう。
ドラクエの“りゅうおう”を表示してみましょう。
以下のような感じで元のデータを表示します。
data = '<<<データのパス>>>/りゅうおう.jpg' image = Image.open(data) image

ここで、PyTorchで処理するために画像データをテンソルに変換します。
その際に画像サイズを128x128に変換し、[0, 1]データを[-1, 1]に変換します。
image_size = 128
transform = Compose([
Resize(image_size), # サイズを小さくする
CenterCrop(image_size), # 128 x 170なので中心を取って128 x 128にする
ToTensor(), # テンソルに変換. これだけだと[0, 1]になっている
Lambda(lambda t: (t * 2) - 1) # [-1, 1]に変換
])
では、このtransformを使って元の画像をテンソルに変換しましょう。これをx_startとします。
x_start = transform(image).unsqueeze(0) # 0次元にバッチ用の次元を追加
この変換したデータをもとにノイズを加えていきますが、ノイズを加えた画像を描画するために画像データに変換するためのreverse_transformを作成します。
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2), # [-1, 1]を[0, 1]に変換
Lambda(lambda t: t.permute(1, 2, 0)), # CHW ⇒ HWC
Lambda(lambda t: t * 255.), # [0, 1] ⇒ [0, 255]
Lambda(lambda t: t.numpy().astype(np.uint8)), # 整数に変換
ToPILImage(), # PILの画像に変換
])
reverse_transformにテンソルに変換したx_startを渡すことで画像に変換されていることを確認します。
squeezeメソッドは、バッチに対応する1次元目を取り除くものです。
reverse_transform(x_start.squeeze())
以下のようにもとに戻っています。少し小さいサイズになっています。

では、元の画像にノイズを加えて表示する関数get_noisy_image()を作成してどのようにノイズが加えられていくかを見てみましょう。
画像x_startという元の画像とtという時点を渡すことで、関数q_sample()によりノイズが付加された画像を生成し、それを画像データに変換して返します。
def get_noisy_image(x_start, t): x_noisy = q_sample(x_start, t, sqrt_alphas_cumprod, sqrt_one_minus_alphas_cumprod) # キレイな画像にタイムステップを渡す noisy_image = reverse_transform(x_noisy.squeeze()) return noisy_image
以下では時点が50の画像を表示します。
t = torch.tensor([49]) noisy_image = get_noisy_image(x_start, t) noisy_image
これを\(t=1, 10, 50, 100, 200\)と表示すると(インデックスではt=0, 9, 49, 99, 199)以下のようになります。

きれいな画像にだんだんノイズが加わって、最後の時点200ではほぼにノイズだけの状態になっています。
正規乱数に従うノイズを加えているので当たり前なのですが、\((1)\)式、\((2)\)式のような確率過程からスタートし、reverse processを求めるというところがこのDiffusion Modelのポイントです。
そして、この逆のreverse processを求めることが学習の目的になります。

損失関数の実装
forward processが実装できたので、そこからreverse processのパラメータ\(\mu_\theta\)を求める必要があります。
(論文では\(\Sigma_\theta\)は確定的としているので\(\Sigma_\theta\)は学習しません)
ここで、平均\(\mu_\theta\)は、
\begin{align}
\mu_\theta({\bf{x}}_t,t)=\frac{1}{\sqrt{\alpha_t}}\left( {\bf{x}}_t -\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta({\bf{x}}_t, t) \right) \tag{8}
\end{align}
と表されます。
ですので、論文では\(\mu_\theta\)を学習するのではなく、\(\epsilon_\theta({\bf{x}}_t, t)\)を求めるように学習します。
(詳細は論文もしくはこちらの記事をご参照ください)
そして、いくつかの単純化を行うことにより、最終的な損失は以下の非常にシンプルな形で表されます。
\begin{align}
L_\text{simple}(\theta)=\mathbb{E}_{t, {\bf{x}}_0, \epsilon}\left[\| \epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon, t) \|^2 \right] \tag{9}
\end{align}
ここで、2項目の\(\epsilon_\theta(\sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon, t)\)は、ノイズのある画像\({\bf{x}}_t\)を使って表すと以下のように表されます。
$$\epsilon_\theta(\sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon, t)=\epsilon_\theta({\bf{x}}_t, t)$$
つまり、ノイズのある画像と時点\(t\)をインプットとして、ニューラルネットワークで処理をするというのが2項目の意味になります。
そして、それがノイズ\(\epsilon\)と近くなるように損失関数を設定しているので、ニューラルネットワークはノイズを含んだ画像からノイズを予測するモデルを学習することになります。
では、この\((9)\)式を実装します。
p_losses()という関数を作成します。
引数のdenoise_modelは次回作成するニューラルネットワークです(U-Netを使います)。
x_startは\({\bf{x}}_0\)を表しています。
def p_losses(denoise_model, x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start)
x_noisy = q_sample(x_start=x_start, t=t, noise=noise) # x_tを計算
predicted_noise = denoise_model(x_noisy, t) # モデルでノイズを予測
loss = F.l2_loss(noise, predicted_noise) # 損失を計算
return loss
ちなみに、Hugging FaceのブログではSmooth L1 Loss(Huber loss)というものを使っています。
基本的には以上でモデル\(\epsilon_\theta\)の学習が可能です。
では、続いてモデルが学習できたとして、そのモデルを使って画像を生成するコードを実装していきましょう。
画像の生成 - Reverse Process
reverse processは、ノイズから画像を生成するプロセスです。
ですので、ランダムなノイズを与えて、そこから実際に画像を生成することができます。
論文では\((4)\)式のreverse processの分散\(\Sigma_\theta\)を\(\sigma_t^2{\bf{I}}\)として定義し、以下のようにしています。
\begin{align}
p_\theta({\bf{x}}_{t-1}| {\bf{x}}_{t})&=N\left({\bf{x}}_{t-1}; \mu_\theta({\bf{x}}_t, t), \sigma_t^2{\bf{I}} \right) \tag{10}\\
\sigma_t^2&=\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_t \tag{11}
\end{align}
\((8)\)式と\((10)\)式、\((11)\)式より、\({\bf{x}}_t\)から\({\bf{x}}_{t-1}\)を求める式は以下になります。
\begin{align}
{\bf{x}}_{t-1}&=\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta({\bf{x}}_t, t)\right) +\sigma_t{\bf{z}} \tag{12} \\
\sigma_t^2&=\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_t \tag{13}\\
{\bf{z}}&\sim N(0,{\bf{I}})
\end{align}
\(\epsilon_\theta({\bf{x}}_t, t)\)はモデルで学習。
モデル\(\epsilon_\theta\)はまだここでは実装せず、次回にUNetを実装したいと思います。
では、まずは\(\sigma_t^2\)を計算します。
\(\bar{\alpha}_t\)と\(\bar{\alpha}_{t-1}\)が必要ですが、\(\bar{\alpha}_t\)は既に計算済みのため、\(\bar{\alpha}_{t-1}\)を計算します。
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
そして、\(\sigma_t^2=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_t\)を計算します。
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)
続いて、\(1/\sqrt{\alpha_t}\)を計算しておきます。
sqrt_recip_alphas = torch.sqrt(1.0 / alphas) # 標準偏差
では、reverse processで\({\bf{x}}_{t}\)から\({\bf{x}}_{t-1}\)を計算するコードを実装します。
modelは学習済みのノイズを予測するモデル\(\epsilon_\theta\)を表し、xは\({\bf{x}}_t\)を表します。
tは時点\(t\)を表していますが、バッチ処理用に配列になっています。
t_indexは配列ではなく時点を表すスカラーです。
@torch.no_grad()
def p_sample(model, x, t, t_index):
# beta_t
betas_t = extract(betas, t, x.shape)
# 1 - √\bar{α}_t
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
# 1 / √α_t
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# μ_Θをモデルで求める: model(x, t)
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
)
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape) # σ^2_tを計算
noise = torch.randn_like(x) # 正規乱数zをサンプリング
return model_mean + torch.sqrt(posterior_variance_t) * noise # x_{t-1}
上記の関数は\({\bf{x}}_t\)から\({\bf{x}}_{t-1}\)を求める関数でしたが、次にループで\({\bf{x}}_T\)から\({\bf{x}}_0\)を求める関数p_sample_loop()を作成します。
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
b = shape[0]
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), total=timesteps):
img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)
imgs.append(img.cupu().numpy())
return imgs
最後にp_sample_loopを呼び出し、実際に画像のサンプルを生成する関数を作成します。
@torch.no_grad() def sample(model, image_size, batch_size=16, channels=3): return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
以上で、Diffusionモデルのパーツの作成は終了です。
あとは、ニューラル・ネットワーク\(\epsilon_\theta\)があれば学習が可能です。
まとめ
今回はDiffusionモデルをPyTorchで実装するために、Diffusionモデルの部分を実装しました。
とりあえずは、forward processを正規分布で定義 ⇒ reverse processも正規分布になる ⇒ reverse processの平均・分散パラメータをニューラル・ネットワークで学習、というメカニズムを理解していただければと思います。
数式を解いた結果だけを載せているので、より詳細が気になる方は本サイトのブログ記事『【論文解説】Diffusion Modelを理解する』、原論文『Denoising Diffusion Probabilistic Models』などをご参照ください。
(まだ、導出過程を載せていない部分もあるので、おいおい載せていきたいとは思っていますが、とりあえずその部分はご自身で計算していただければと思います…)
あとは、ノイズを除去するモデル\(\epsilon_\theta\)と実際に学習・生成する部分の実装が必要になりますが、前者については次回にUNetを実装し、後者についてはその次に実装したいと思います。
では!!
