GLIDE や SR3 などといったモデルで使われており、最近よく見かけるようになった Diffusion Model の解説をしたいと思います。
diffusion model はもともと2015年に『Deep Unsupervised Learning using Nonequilibrium Thermodynamics』という論文で提案されています。
その後、今回紹介する『Denoising Diffusion Probabilistic Models』という論文が2020年に公開され、Denoising Diffusion Model として改良されました。
こちらの diffusion model は Denoising Diffusion Probabilistic Model から DDPM と表記されることもあります。
ということで、今回はこちらの論文をメインに解説したいと思います。
『Denoising Diffusion Probabilistic Models』
理解が浅い部分があるかもしれないので、間違いがあればご指摘ください!!
また、以下の記事では、PyTorch を使って Diffusion モデルを実装していますので、こちらもあわせて参考にしていただければと思います。
目次
Diffusion Model の概要
まずは、diffusion model のざっくりとした概要について説明したいと思います。
forward process と reverse process
diffusion model は、以下の図のように(1) forward process と(2) reverse process の2つの過程を考えます。
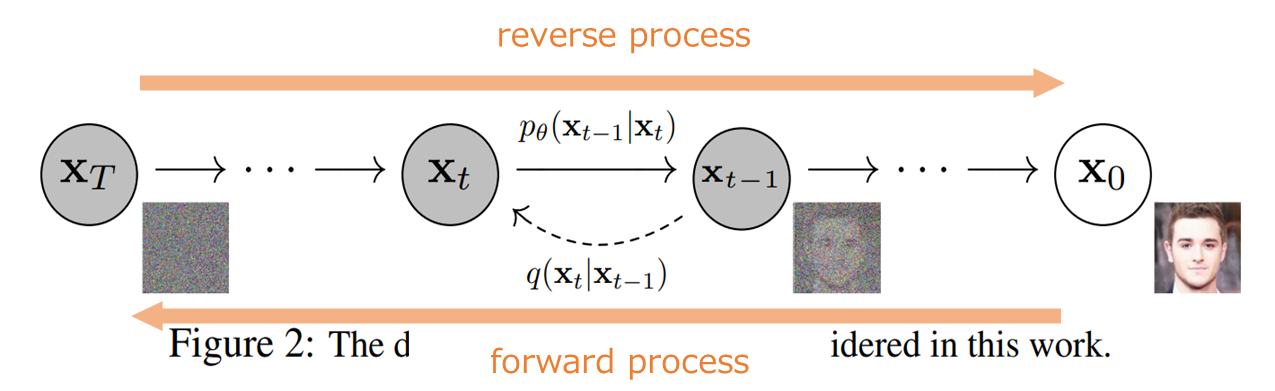
forward process は画像にノイズを加えていって、最終的にはノイズだけになる確率過程です。
一方の reverse process は forward process の逆で、ノイズから画像になっていく確率過程です。
つまり、画像にノイズを加えていって、最終的にノイズのみになる確率過程を考え、その逆をたどることでノイズから画像を生成することができる、というものです。
こちらはさらにざっくりイメージです。
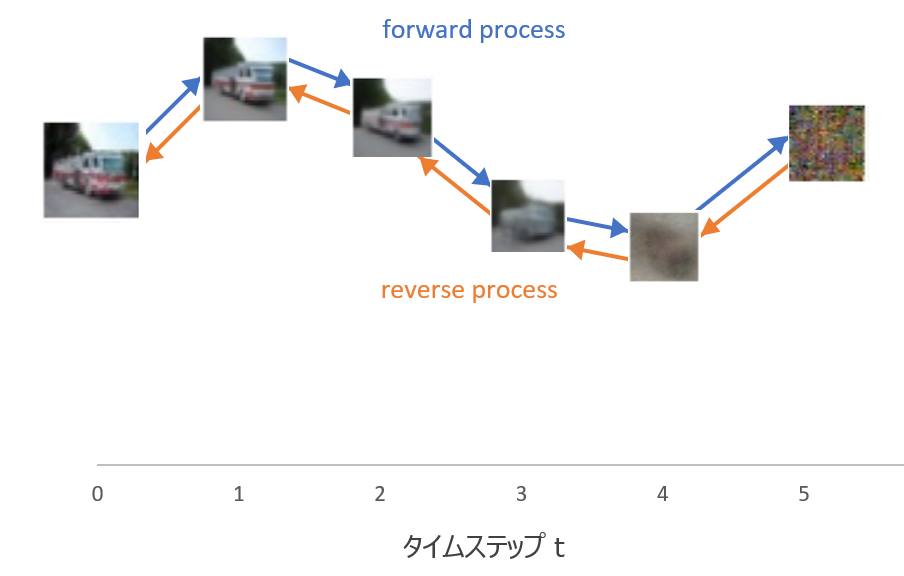
上記の図で言うと、forward process は \({\bf{x}}_0\) にノイズを加えて \({\bf{x}}_1\)、\({\bf{x}}_2\)、...となり、最終的に \({\bf{x}}_T\) というノイズだけになります。
reverse process はその逆をたどり、ノイズ \({\bf{x}}_T\) から画像 \({\bf{x}}_0\) を生成します。
\({\bf{x}}_T\) を平均ゼロ、分散1の標準正規分布とすることで、標準正規分布に従うノイズから画像を生成することができます。
こちらは、『Deep Unsupervised Learning using Nonequilibrium Thermodynamics』からの図ですが、一番上は forward process で \(t=0\) からノイズが加わって、\(t=T\) では完全なノイズになっています。
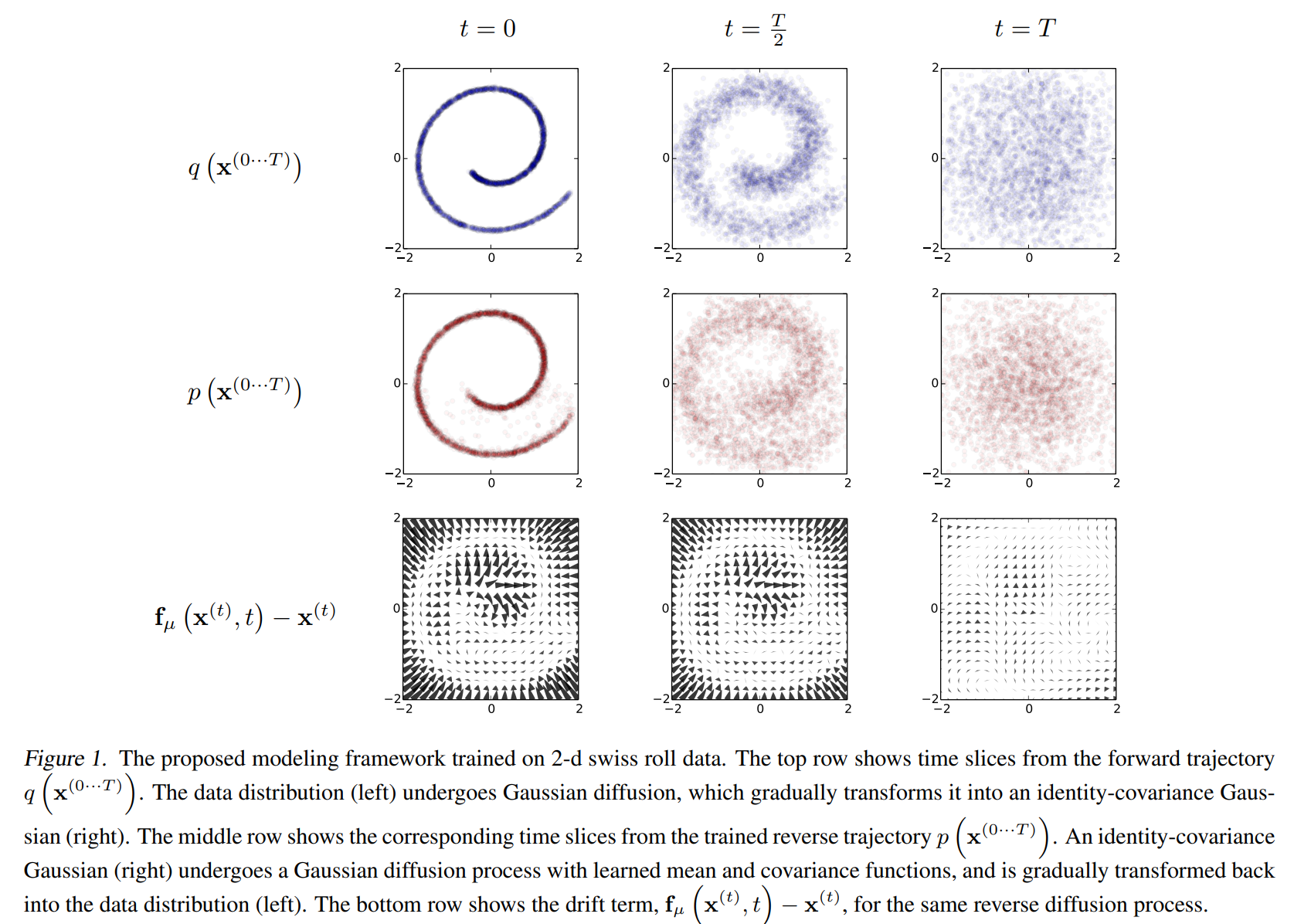
2段目は reverse process で、\(t=T\) からスタートし、\(t=0\) で多少ノイズは残るものの上段の \(t=0\) の図を再現できています。
また、一番下はノイズに当たります。
VAE との関連性
観測されるデータは \({\bf{x}}_0\) になり、それ以外の \({\bf{x}}_1, \cdots, {\bf{x}}_T\) は潜在変数と考えます。
ですので、diffusion model は VAE などと同じように潜在変数の存在する生成モデルということです。
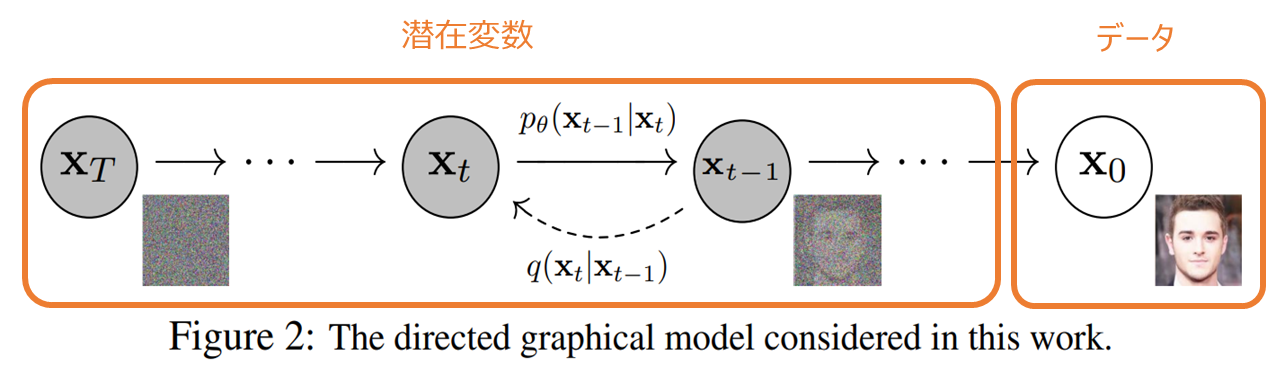
そのため、目的関数は基本的には VAE と同様に下界の最大化です。
基本的にはと言ったのは、最終的には下界を非常に単純化して計算される損失関数を最小化していきます。
diffusion model の仕組み
では、概要を把握したところで、詳細に入っていきたいと思います。
確率過程
forward process
まず、forward process (diffusion process とも言う)、つまり真の値にノイズが加わっていく過程は以下のマルコフ連鎖で定義されます。
$$\begin{align}
q_\theta({\bf{x}}_{1:T}|{\bf{x}}_{0}):&=\prod^T_{t=1}q({\bf{x}}_{t}|{\bf{x}}_{t-1}),\tag{1}\\
q({\bf{x}}_{t}|{\bf{x}}_{t-1})&=N({\bf{x}}_{t}; \sqrt{1-\beta_t }{\bf{x}}_{t-1}, \beta_t {\bf{I}}) \tag{2}
\end{align}$$
上記の式は以下の2点を表しています。
- 独立性もしくはマルコフ性(上段の式)
\({\bf{x}}_{0}\) というデータに対して、\({\bf{x}}_{1}, {\bf{x}}_{2}, \cdots\) という潜在変数が生成されますが、\({\bf{x}}_{t}\) の分布は \({\bf{x}}_{t-1}\ )の値にのみ依存します。 - 正規分布に従う(下段の式)
\(q({\bf{x}}_{t}|{\bf{x}}_{t-1})\) は平均 \(\sqrt{1-\beta_t {\bf{x}}_{t-1}}\)、分散 \(\beta_t {\bf{I}}\) の正規分布に従うということです。
ここで、\(\beta_t\) は各ステップごとに違ってきて、学習パラメータとすることも可能ですが、実験によると定数として決め打ちしてしまっても問題ないことがわかったとのことです。
ですので、forward process については、学習するパラメータはありません。
reverse process
続いて、reverse process です。
reverse は以下のように定義します。
$$\begin{align}
p_\theta({\bf{x}}_{0:T}):&=p_\theta({\bf{x}}_{T})\prod^T_{t=1}p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t}), \tag{3}\\
p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})&=N\left({\bf{x}}_{t-1}; \mu_\theta({\bf{x}}_t, t), \Sigma_\theta({\bf{x}}_t, t)\right) \tag{4}
\end{align}$$
forward process と同様に、\({\bf{x}}_{t-1}\) の分布は \({\bf{x}}_{t}\) の値にのみ依存し(マルコフ性)、\(p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})\) も正規分布に従うということになります。
VAE と同じように、この正規分布の平均・分散をニューラルネットワークで求めます(最終的には分散は固定値にし、平均を求める代わりに誤差を求める問題に置き換わります)。
forward process と reverse process の関係
ここで、forward process、reverse process ともに正規分布に従うという仮定を置いていますが、それは良いのでしょうか?
実は、forward process の分散が小さい場合、つまり拡散が小さい場合、その逆の過程である reverse process も同じ関数形を取ることがわかっています。
ですので、\(\beta_t\) を小さくとると、reverse process も同じ正規分布となることが保証されます。
目的関数
目的関数は、対数尤度 \(\log p_\theta({\bf{x}}_0)\) を最大化することを考えますが、VAE (Variational Auto-Encoder) で見たように、ニューラルネットワークを使った潜在変数が存在するような複雑なモデルで対数尤度を最大化するのは簡単ではありません。
そこで、VAE と同様に変分推論の考え方を利用し、変分下界 (Variational Lower Bound) を最大化します。
潜在変数を \({\bf{z}}\)、観測データを \({\bf{x}}\) とした場合、下界 \(\mathcal{L}\) は以下で表されます。
$$\begin{align}
\mathcal{L}:= \mathbb{E}_{q({{\bf{z}}|\bf{x}})}\left[\log \frac{p({\bf{x}}, {\bf{z}})} { q({\bf{z}}| {\bf{x}})} \right]
\end{align}$$
この下界は対数周辺尤度の下界になっています。
$$\begin{align}
\log p({\bf{x}}) \ge \mathcal{L}
\end{align}$$
対数尤度は求まらないけど、対数尤度はこれよりは大きいという下界であれば求められ、その下界を最大化することで対数尤度を最大化しましょう、というものです。
下界の計算方法の詳細についてはここでは省略しますので、こちらのVAEの記事をご参照ください。
では、これを diffusion process に当てはめましょう。
潜在変数は \({\bf{x}}_{1:T}\)、データは \({\bf{x}}_0\) なので、潜在変数とデータの同時分布は \({\bf{x}}_{0:T}\) で表されますので、
$$\begin{align}
\log p_\theta({\bf{x}}_0)&\ge \mathbb{E}_{q({{\bf{x}}_{1:T}|\bf{x}}_0)}\left[\log \frac{p_\theta({\bf{x}}_{0:T})} { q({\bf{x}}_{1:T}| {\bf{x}}_0)} \right]=:\mathcal{L}
\end{align}$$
となります。
ここでは一つのデータ\({\bf{x}}_0\)に対する周辺対数尤度を考えており、最終的にはデータに関して期待値 \(\mathbb{E}\) を取る必要があり、論文ではそのような表記になっていますのでご留意ください。
ここで、\((1)\)式と\((3)\)式を代入して変形すると、
$$\begin{align}
\mathcal{L}&=\mathbb{E}_{q({{\bf{x}}_{1:T}|\bf{x}}_0)}\left[\log \frac{p({\bf{x}}_T)\prod_{t=1}^T p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})} { \prod_{t=1}^T q({\bf{x}}_{t}| {\bf{x}}_{t-1})} \right] \\
&=\mathbb{E}_{q({{\bf{x}}_{1:T}|\bf{x}}_0)}\left[\log p({\bf{x}}_T) + \sum_{t\ge 1}\log \frac{p_\theta({\bf{x}}_{t-1}|p_\theta({\bf{x}}_t))}{q_\theta({\bf{x}}_{t}|q_\theta({\bf{x}}_{t-1}))} \right]
\end{align}$$
と表されます。
ここで、下界\ (\mathcal{L}\ )の最大化ではなく負の下界の最小化を考えるために
$$\begin{align}
L&=-\mathcal{L}\\
&=-\mathbb{E}_{q({{\bf{x}}_{1:T}|\bf{x}}_0)}\left[\log p({\bf{x}}_T) + \sum_{t\ge 1}\log \frac{p_\theta({\bf{x}}_{t-1}|p_\theta({\bf{x}}_t))}{q_\theta({\bf{x}}_{t}|q_\theta({\bf{x}}_{t-1}))} \right] \tag{5}
\end{align}$$
として考えていきます。
単純化した目的関数
これが下界を表す式になるので、これを最大化すればいいのですが、ここからゴリゴリ計算をしたり、単純化することにより非常にすっきりとしたシンプルな式に変形します。
最終形はこのような式になります(計算過程についてはこれから説明します)。
$$L_\text{simple}(\theta)=\mathbb{E}_{{\bf{t}}, {\bf{x}}_0, {\bf{\epsilon}}}\left[\| \epsilon-\epsilon_\theta \left(\sqrt{\bar{\alpha}}{\bf{x}}_0
+\sqrt{1-\bar{\alpha}_t}\epsilon, t \right) \|^2\right] \tag{6}$$
非常にシンプルな式になっていますね。
なお、この式はデータに関して平均を取った形の最終形です。
\(\epsilon_\theta\) がニューラルネットワークになっています。
ざっくりとした解釈としては、各タイムステップ \(t\)、データ \({\bf{x}}_0\) に対してノイズである乱数 \(\epsilon\) を振り、ノイズを加えた画像データとタイムステップ \(t\) をインプットとして、\(\epsilon\) を再構築するようなニューラルネットワークのパラメータ \(\theta\) を学習していきます。
アルゴリズム
イメージをつかむために先に学習アルゴリズムを軽く見てみましょう。
\({\bf{x}}_0\) をデータから取ってきて、タイムステップ \(t\) を1から \(T\) から一つ選びます。
そして、標準正規分布に従う \(\epsilon\) を振り、ニューラルネットワークで \(\epsilon_\theta\) を求め、\((6)\) 式の勾配を計算してパラメータを更新していきます。

学習が終了しパラメータ \(\theta\) が決まったあとにサンプリングする際には、reverse process を使います。
アルゴリズムは以下のように、\({\bf{x}}_T~N({\bf{0}}, {\bf{I}})\) で生成し、\(T\) から1まで学習した reverse process で \({\bf{x}}_0\) を求めていきます。

目的関数の単純化
では、ここからは一つのデータに対する下界である \((5)\) 式から単純化した損失関数 \((6)\) 式を導出していきたいと思います。
まず、\(q({\bf{x}}_t|{\bf{x}}_{0})\) を求めていきましょう。
これがわかれば、データ \({\bf{x}}_0\) が与えられた場合の \({\bf{x}}_t\) の分布がわかります。
\({\bf{x}}_{t-1}\) が与えられた場合、forward process \((2)\) 式から、
$${\bf{x}}_t=\sqrt{1-\beta_t}{\bf{x}}_{t-1}+\sqrt{\beta_{t}}\epsilon_{t} , \hspace{10pt} \epsilon~N({\bf{0}},{\bf{I}})$$
と表されます。
これを繰り返すと、
$$\begin{align}
{\bf{x}}_t&=\sqrt{1-\beta_t}{\bf{x}}_{t-1}+\sqrt{\beta_{t}}\epsilon_{t} \\
&=\sqrt{1-\beta_t}\left(\sqrt{1-\beta_{t-1}}{\bf{x}}_{t-2}+\sqrt{\beta_{t-1}}\epsilon_{t-1}\right)+\sqrt{\beta_{t}}\epsilon_{t}\\
&=\sqrt{1-\beta_t}\sqrt{1-\beta_{t-1}}{\bf{x}}_{t-2}+\sqrt{1-\beta_t}\sqrt{\beta_{t-1}}\epsilon_{t-1}+\sqrt{\beta_{t}}\epsilon_{t}\\
&=...\\
&={\bf{x}}_0\prod_{i=1}^t\sqrt{1-\beta_i}+\sum^t_{i=1}\left(\sqrt{\beta_i}
\prod_{j=i+1}^{t}\sqrt{1-\beta_j}\right)\epsilon_j
\end{align}$$
と表されます。
ここから、平均 \(\mu_t\) は、
$$\begin{align}
\mu_t=\prod_{i=1}^t \sqrt{1-\beta_i}{\bf{x}}_0
\end{align}$$
となります。
$$\begin{align}
\alpha_t&=1-\beta_t,\\
\bar{\alpha}_t&=\prod_{s=1}^t\alpha_s
\end{align}$$
とすると、
$$\begin{align}
\mu_t&=\prod_{i=1}^t \sqrt{\alpha_i}=\sqrt{\prod_{i=1}^t\alpha_i}=\sqrt{\bar{\alpha}_t}{\bf{x}}_0
\end{align}$$
となります。
分散については、
$$\begin{align}
\Sigma_t&=\sum_{i=1}^t\left(\sqrt{\beta_i}\prod_{j=i+1}^t\sqrt{1-\beta_j}\right)^2\\
&=\sum_{i=1}^t\left(\beta_i\prod_{j=i+1}^t(1-\beta_j)\right)\\
&=\sum_{i=1}^t\left((1-\alpha_i)\prod_{j=i+1}^t\alpha_j\right)\\
&=\sum_{i=1}^t\left(\prod^t_{j=i+1}\alpha_{j}-\prod^t_{j=i}\alpha_j \right)\\
&=\sum_{i=1}^t\left(\alpha_{i+1, t}-\alpha_{i,t}\right)\\
&=\alpha_{t+1,t}-\alpha_{1,t}\\
&=1-\prod^t_{i=1}\alpha_i\\
&=1-\bar{\alpha}_t
\end{align}$$
と表すことができます。
変形の途中では、
$$\alpha_{i,t}=\prod^t_{j=1}\alpha_j$$
としています。
以上より、
$$q({\bf{x}}_t|{\bf{x}}_0)=N\left({\bf{x}}_t; \sqrt{\bar{\alpha}_t}{\bf{x}}_0, (1-\bar{\alpha}_t){\bf{I}}\right) \tag{7}$$
が求まります。
この式により、データ \({\bf{x}}_0\) に対し、ステップ \(t\) における \({\bf{x}}_t\) を求めることができます。
この式はあとで出てきます。
次に、目的関数 \((5)\) 式を変形していきます。
\((5)\) 式で \(t=1\) のときだけ取り出すと
$$\begin{align}
\text{(5)式} &= -\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log p({\bf{x}}_T)+\sum_{t>1}\log\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t}|{\bf{x}}_{t-1})}
+ \log\frac{p_\theta({\bf{x}}_{0}|{\bf{x}}_1)} {q({\bf{x}}_{1}|{\bf{x}}_{0})} \right]
\end{align}$$
となります。
ここで、
$$\begin{align}
q({\bf{x}}_{t}|{\bf{x}}_{t-1})&=q({\bf{x}}_{t}|{\bf{x}}_{t-1}, {\bf{x}}_{0})\\
&=\frac{q({\bf{x}}_{t}, {\bf{x}}_{t-1}|{\bf{x}}_{0})}{q({\bf{x}}_{t-1}|{\bf{x}}_{0})}\\
&=q({\bf{x}}_{t-1}|{\bf{x}}_{t},{\bf{x}}_{0})\frac{q({\bf{x}}_{t}|{\bf{x}}_{0})}{q({\bf{x}}_{t-1}|{\bf{x}}_{0})}
\end{align}$$
という関係を使って変形すると、
$$\begin{align}
\text{(5)式} &=-\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log p({\bf{x}}_T)+
\sum_{t>1}\log\left(\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})}
\frac{q({\bf{x}}_{t-1}|{\bf{x}}_{0})}{q({\bf{x}}_{t}|{\bf{x}}_{0})}\right)
+ \log\frac{p_\theta({\bf{x}}_{0}|{\bf{x}}_1)} {q({\bf{x}}_{1}|{\bf{x}}_{0})} \right] \\
&=-\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log p({\bf{x}}_T)+
\sum_{t>1}\log\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})}
+\sum^T_{t>1} \left(\log q({\bf{x}}_{t-1}|{\bf{x}}_{0}) -\log q({\bf{x}}_{t}|{\bf{x}}_{0})\right)
+ \log\frac{p_\theta({\bf{x}}_{0}|{\bf{x}}_1)} {q({\bf{x}}_{1}|{\bf{x}}_{0})} \right] \\
&=-\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log\frac{ p({\bf{x}}_T)}{q({\bf{x}}_T|{\bf{x}}_0)}+
\sum_{t>1}\log\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})}
+ \log p_\theta({\bf{x}}_0|{\bf{x}}_1) \right] \\
&=D_\text{KL}\left(q({\bf{x}}_T|{\bf{x}}_0)\|p({\bf{x}}_T)\right)
+\sum_{t>1}\mathbb{E}_{q({\bf{x}}_{t}|{\bf{x}}_0)}\left[D_\text{KL}\left(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\| p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{0})\right) \right]\\
&\hspace{2pt}-\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log p_\theta({\bf{x}}_0|{\bf{x}}_1)\right] \tag{8}
\end{align}$$
と変形できます。
ここで、3行目は
$$\sum^T_{t>1} \left(\log q({\bf{x}}_{t-1}|{\bf{x}}_{0}) -\log q({\bf{x}}_{t}|{\bf{x}}_{0})\right)-\log q({\bf{x}}_1|{\bf{x}}_0)=-\log q({\bf{x}}_T|{\bf{x}}_0)$$
となることを使っています。
また、最後の行の2項目は、
$$\begin{align}
\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})}\right]&=
\int \log\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})}q({\bf{x}}_{1:T}|{\bf{x}}_{0})d{\bf{x}}_{1:T}\\
&=\int \log\frac{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)} {q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})}q({\bf{x}}_{t\neq t}|{\bf{x}}_{0},{\bf{x}}_{t})q({\bf{x}}_{t}|{\bf{x}}_{0})d{\bf{x}}_{1:T}\\
&=\int D_\text{KL}\left(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\| p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{0})\right)q({\bf{x}}_{t}|{\bf{x}}_{0})d{\bf{x}}_{t}\\
&=\mathbb{E}_{q({\bf{x}}_{t}|{\bf{x}}_0)}\left[D_\text{KL}\left(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\| p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{0})\right) \right]
\end{align}$$
としています。
なお、カルバック・ライブラー・ダイバージェンスは以下で表されますのでご参考まで。
$$D_\text{KL}(q|p)=\mathbb{E}_q\left[\log\frac{q(X)}{p(X)}\right]$$
そして、論文では上記の3つの項に分けています。
$$\begin{align}
L_T&=D_\text{KL}\left(q({\bf{x}}_T|{\bf{x}}_0)\|p({\bf{x}}_T)\right)\\
L_{t-1}&=\mathbb{E}_{q({\bf{x}}_{t}|{\bf{x}}_0)}\left[D_\text{KL}\left(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\| p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})\right)\right] \\
L_0&=\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log p_\theta({\bf{x}}_0|{\bf{x}}_1)\right]
\end{align}$$
こう置くことにより、
$$(5)式=L_T+\sum_{t>1}L_{t-1}-L_0 \tag{9}$$
と表されます。
\(L_T\) については、\(\theta\) が出てきていないのでニューラルネットワークは関係ありません。
そして、\(\beta_t\) を固定値とすると、パラメータがないので \(L_T\) については無視してよいとことになります。
ですので、\(L_{1:T-1}\) と \(L_0\) について見ていきましょう。
\(L_{1:T-1}\)
上述の通り、\(L_{t-1}\) は以下のように表されます。
$$L_{t-1}=\mathbb{E}_{q({\bf{x}}_{t}|{\bf{x}}_0)}\left[D_\text{KL}\left(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\| p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})\right)\right]$$
\(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\)と\(p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})\) のカルバック・ライブラー・ダイバージェンスです。
(5) 式を見ていただくと、\(D_\text{KL}\) にマイナスの符号がついているので (5) 式を最大化することは \(D_\text{KL}\) を最小化することと同義になります。
1st step
ここで、\(p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})\) は reverse process の確率過程で、
$$p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})=N\left({\bf{x}}_{t-1}; \mu_\theta({\bf{x}}_t, t), \Sigma_\theta({\bf{x}}_t, t)\right)$$
と定義されていました。
\(\mu_\theta\) と \(\Sigma_\theta\) はニューラルネットワークで求める必要がありますが、ここで \(\Sigma_\theta\) をニューラルネットワークで計算しない \(\sigma_t^2{\bf{I}}=\beta_t{\bf{I}}\) として、簡略化します。
つまり、forward process と同じ分散としています。
実験の結果では、この仮定をおいてもパフォーマンスへの影響はあまりなかったようです。
2nd step
つづいて、あとで使うために \(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\) を計算しておきます。
こちらは以下のように計算できます。
$$\begin{align}
q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})&=N\left({\bf{x}}_{t-1}; \tilde{\mu}_t({\bf{x}}_t, {\bf{x}}_0), \tilde{\beta}_t{\bf{I}}\right)
\end{align}$$
ここで、\(\tilde{\mu}_t\)と\(\tilde{\beta}_t\) は次で表されます。
$$\begin{align}
\tilde{\mu}_t({\bf{x}}_t, {\bf{x}}_0)&=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}{\bf{x}}_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}{\bf{x}}_t \tag{10}\\
\tilde{\beta}_t &= \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t \tag{11}
\end{align}$$
ちょっと大変そうなのでまだ計算していませんが、どこかのタイミングで確認して投稿したいと思います。
3rd step
この2つの式を使って、\(L_{t-1}\) を変形します。
まず、\(p(x)~N(\mu_p, \sigma^2_p)\)、\(q(x)~N(\mu_q, \sigma^2_q)\) の場合にその2つの分布の KL ダイバージェンスは、
$$\begin{align}
D_\text{KL}\left(q\|p\right)&=\int q(x)\log\frac{q(x)}{p(x)}dx \\
&=\log \frac{\sigma_p}{\sigma_q} +\frac{\sigma_q^2+(\mu_q-\mu_p)^2}{2\sigma_p^2}-\frac{1}{2} \\
&= \frac{(\mu_q-\mu_p)^2}{2\sigma_p^2}+C \tag{12}
\end{align}$$
と計算できることを使います。
\(C\) は \(\mu_p\) を含まない項がまとめられています。
この計算はあとで載せておきますが(初回の投稿では載せていないかもしれません)、頑張って計算すれば求まります。
そして、それぞれ \(\mu_p=\mu_\theta({\bf{x}}_t, t)\)、\(\sigma_p^2=\beta_t=\sigma_t^2\)、\(\mu_q=\tilde{\mu}({\bf{x}}_t, {\bf{x}}_0)\) なので、
$$\begin{align}
L_{t-1}&=\mathbb{E}_{q({\bf{x}}_{t}|{\bf{x}}_0)}\left[D_\text{KL}\left(q({\bf{x}}_{t-1}|{\bf{x}}_{t}, {\bf{x}}_{0})\| p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})\right)\right] \\
&= \mathbb{E}_{q({\bf{x}}_{t}|{\bf{x}}_0)}\left[\frac{1}{2\sigma^2_t}\| \tilde{\mu}({\bf{x}}_t, {\bf{x}}_0) - \mu_\theta({\bf{x}}_t, t)\|^2\right] + C \tag{13}
\end{align}$$
となります。
上記のカルバック・ライブラー・ダイバージェンスは、二つの正規分布の平均パラメータの2乗誤差に比例することがわかります。
すっきりしてきましたね。
4th step
上記の \(L_{t-1}\) を使って計算しても良いのですが、さらに単純化を行います。
前に求めた \((7)\) 式は、
$$q({\bf{x}}_t|{\bf{x}}_0)=N\left(\sqrt{\bar{\alpha}_t}{\bf{x}}_0, (1-\bar{\alpha}_t){\bf{I}}\right)$$
でした。
ここから、
$${\bf{x}}_t=\sqrt{\bar{\alpha}_t}{\bf{x}}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$$
と表されます。
なので、\((13)\) 式の \({\bf{x}}_0\)を\({\bf{x}}_t\) で表すようにすると、
$$L_{t-1}-C= \mathbb{E}_{{\bf{x}}_0, \epsilon}\left[\frac{1}{2\sigma^2_t}\left\| \tilde{\mu}\left({\bf{x}}_t, \frac{1}{\sqrt{\bar{\alpha}_t}}\left({\bf{x}}_t({\bf{x}}_0, \epsilon)-\sqrt{1-\bar{\alpha}_t}\epsilon\right)\right) - \mu_\theta({\bf{x}}_t, t)\right\|^2 \right]$$
となります。
\({\bf{x}}_t\)は\({\bf{x}}_0\) と \(\epsilon\) の関数になっています。
ここで、\(\tilde{\mu}\) に \((10)\) 式で表されるので、\((10)\) 式を使って変形すると、
$$L_{t-1}-C= \mathbb{E}_{{\bf{x}}_0, \epsilon}\left[\frac{1}{2\sigma^2_t}\left\| \frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t({\bf{x}}_0, \epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon\right)- \mu_\theta({\bf{x}}_t, t)\right\|^2 \right] \tag{14}$$
となります。
大変ではありますが、代入して計算するだけですので、途中式は記載しませんが(これもいつか掲載するかもしれません)、
$$\beta_t=1-\alpha_t$$
$$\bar{\alpha}_t=\prod_{s=1}^t\alpha_s \hspace{10pt} \Rightarrow \hspace{10pt} \frac{\bar{\alpha}_{t-1}}{\bar{\alpha}_{t}}=\frac{1}{\alpha_t}$$
といった関係を使えば求まります。
5th step
\((14)\) 式より、\(\mu_\theta\) は \(\tilde{\mu}_t({\bf{x}}_t, \epsilon)\) を変形した
$$\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t({\bf{x}}_0, \epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon\right)$$
を予測すればよいことになります。
ここから、関数 \(\mu_\theta\) が \((15)\) 式に近くなるためには、\({\bf{x}}_t\) がインプットなので既知であることから、
$$\mu_\theta({\bf{x}}_t, t)=\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t({\bf{x}}_0, \epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta({\bf{x}}_t, t))\right) \tag{15}$$
とすればよいと考えられます。
\(\epsilon_\theta({\bf{x}}_t, t)\) とすることで \(\epsilon\) を \({\bf{x}}_t\) と \(t\) をインプットとするパラメータが\(\theta\)の関数とします。
これで \(\mu_\theta\) が求まり、分散は \(\sigma^2_t\) と置いているので、reverse process の分布 \(p({\bf{x}}_{t-1}|{\bf{x}}_{t})\) が求まりました。
ですので、\({\bf{x}}_t\) が与えられたときの \({\bf{x}}_{t-1}\) は
$${\bf{x}}_{t-1}=\mu_\theta({\bf{x}}_{t},t) + \sigma_t {\bf{z}}, \hspace{10pt} z\sim N({\bf{0}}, {\bf{I}})$$
でサンプリングすることができます。
そして、\((15)\) 式を \((14)\) 式に代入して整理すると、
$$\frac{\beta_t^2}{2\sigma^2_t\alpha_t(1-\bar{\alpha}_t)}\left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t \right) \right\|^2 \tag{16}$$
と単純化することができます。
\((14)\) 式は \(\tilde{\mu}\) をニューラルネットワークで予測する問題でしたが、\((16)\) 式では \(\epsilon\) を予測する問題になりました。
どちらの方法でも良いのですが、あとで行う実験では \(\epsilon\) を予測する後者の問題を解く方が精度が良かったということです。
あとで、この式をもう少しだけ単純化し、それがさらに良い精度になったということです。
\(L_0\)
次に \(L_0\) を見ていきます。
\(L_0\) は
$$L_0=\mathbb{E}_{q({\bf{x}}_{1:T})|{\bf{x}}_0}\left[\log p_\theta({\bf{x}}_0|{\bf{x}}_1)\right]$$
です。
\({\bf{x}}_1\) から \({\bf{x}}_0\) を生成する、つまり潜在変数から画像を生成する部分に当たるのでデコーダの項になります。
デコーダですので、PixelCNN などをデコーダとして使うことも一つですが、ここではシンプルに正規分布の確率計算にしています。
インプットの \(\{0, \cdots, 255\}\) を \([-1,1]\) にスケーリングしているものと仮定しておきます。
$$\begin{align}
\log p_\theta({\bf{x}}_0|{\bf{x}}_1)&=\prod^D_{i=1}\int^{\delta_+(x_0^i)}_{\delta_-(x_0^i)}N(x;\mu_\theta^i({\bf{x}}_1,1),\sigma_1^2)dx
\end{align}$$
ここで、
$$\begin{align}
\delta_+(x_0^i)&=\left\{ \begin{array}{l, l}\infty & \hspace{10pt}\text{if }x=1\\ x+\frac{1}{255} & \hspace{10pt}\text{if }x<1 \end{array}\right.,
\delta_-(x_0^i)&=\left\{ \begin{array}{l, l}-\infty & \hspace{10pt}\text{if }x=-1\\ x-\frac{1}{255} & \hspace{10pt}\text{if }x>-1 \end{array}\right.
\end{align}$$
です。
\(D\) は \({\bf{x}}\) の次元です。
\(t=1\) なので正規分布の平均は \(\mu_\theta({\bf{x}}_1, 1)\) になっています。
これは単に分布関数 \(N\) を使って \((x-\frac{1}{255},x+\frac{1}{255})\) の区間で面積を計算し、(同時) 確率を求めているだけです。
いずれにせよ、さらに単純化した最終形ではこちらは使いません。
さらに単純化
以下の \((16)\) 式は、\(\epsilon\) をニューラルネットワークで予測した際の誤差をタイムステップに応じて重みづけしていることになります。
$$\frac{\beta_t^2}{2\sigma^2_t\alpha_t(1-\bar{\alpha}_t)}\left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t \right) \right\|^2$$
論文では、重みづけをしない形にして、
$$\left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t \right) \right\|^2$$
と単純化します。
実験の結果では、このように単純化した方が精度が改善していますので、あとで確認したいと思います。
そして、最終的な損失関数は、タイムステップ \(t\)、データ \({\bf{x}}_0\)、乱数 \(\epsilon\) で平均を取ります。
$$L_\text{simple}(\theta)=\mathbb{E}_{t,{\bf{x}}_0, \epsilon}\left[\left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t \right) \right\|^2\right] \tag{17}$$
以上で、この論文において最も精度が良かった損失関数を求めることができました。
\(t=1\) の場合が \(L_0\) に対応しますが、この単純化した損失関数では \(L_0\) の議論はまったく出てこず、\(t>1\) の場合と同様に計算します。
実験
タイムステップは \(T=1000\) とします。
ニューラルネットワークの部分は U-Net を使用します。
U-Net の論文はこちらです。
『U-Net: Convolutional Networks for Biomedical Image Segmentation』
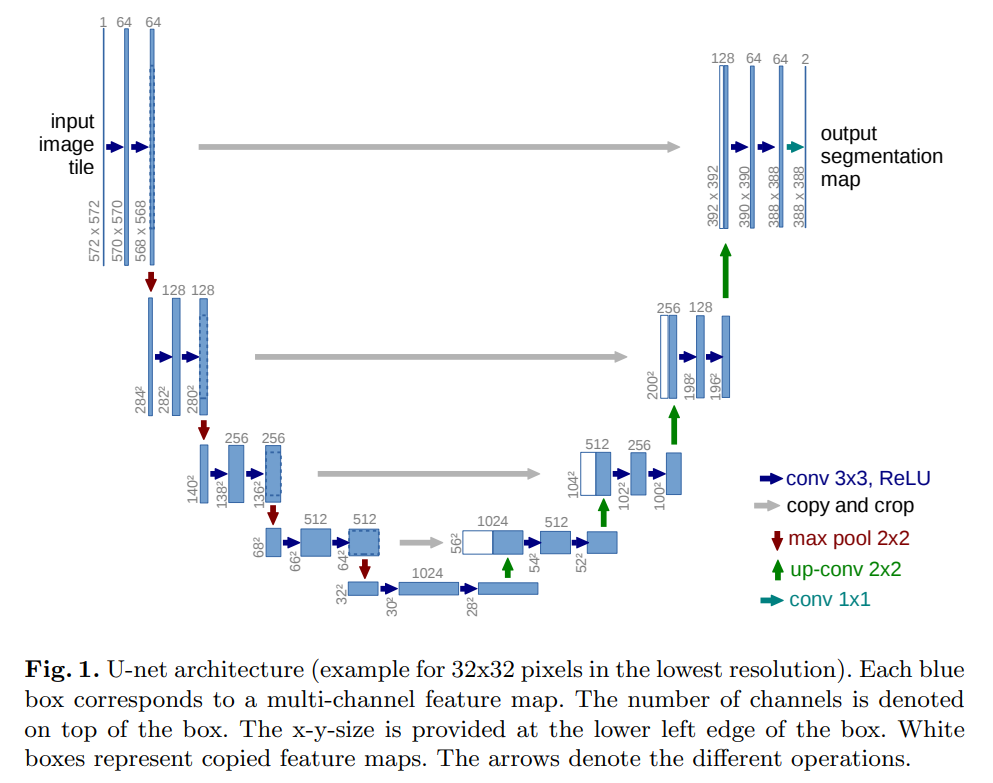
U-Net の詳しい説明は割愛しますが、上図のようにインプットを小さいサイズに圧縮し戻していくモデルです。
その際に同じサイズ同士でスキップ・コネクションにより連結するという特徴があります。
U-Net については、こちらの記事で実装していますので参考にしてみてください ⇒ 『DiffusionモデルをPyTorchで実装する② ~ U-Net編』。
(Cousera の GAN コースでも解説されています。 ⇒ 【Cousera講座レビュー】DeepLearning.ai『Generative Adversarial Networks(GANs)』)
さらに Transformer で使われていた sin 関数を使った position embedding を使用し、self-attention を使ったモデルとします。
そして、\(\beta_1=10^{-4}\)、\(\beta_T=0.02\)としています。
この \(\beta\) を十分に小さくすることで、forward process と reverse process が同じ関数形で近似できます。
結果
では実験結果を見ていきましょう。
CIFAR10での精度
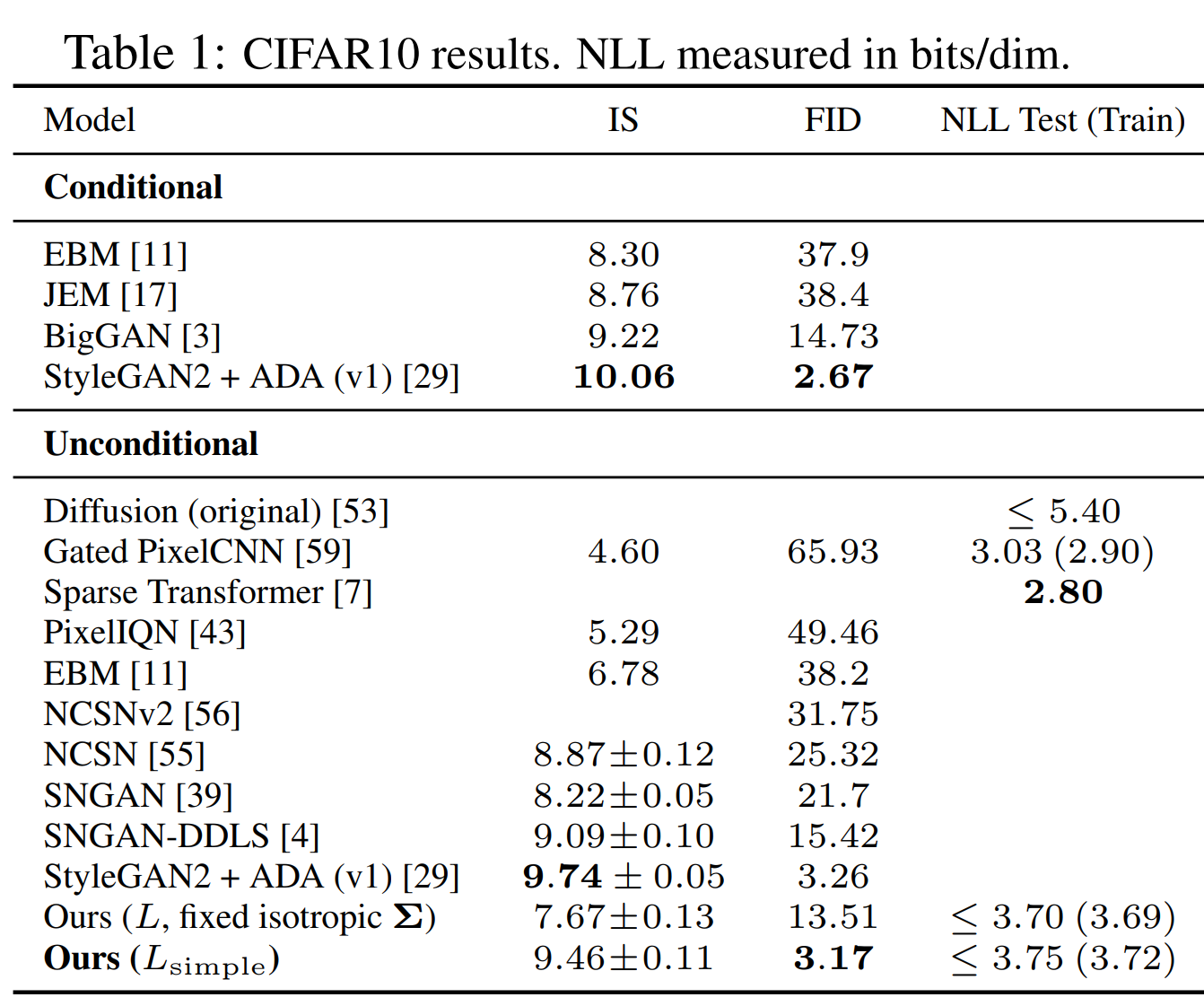
CIFAR10 データセットを使った結果です。
\(L_\text{simple}\) を損失関数とした場合において、IS (Inception スコア) は StyleGAN には及びませんが、FID に関しては StyleGAN を上回っており、非常に良い結果となっています。
ちなみに、Inception スコアは高ければ良い指標、FID は低ければ良い指標になります。
それぞれの詳細は『Inception Scoreを理解する』と『Frechet Inception Distanceを理解する』をご参照ください。
ラベルを指定して生成する Conditional と比較しても一番ではありませんが悪くない結果です。
生成された画像
以下は LSUN データセットで学習して、生成された画像です。
非常にキレイですね。

損失関数の比較
続いて、損失関数を単純化する影響について見ていきます。
結果は以下のようになっています。
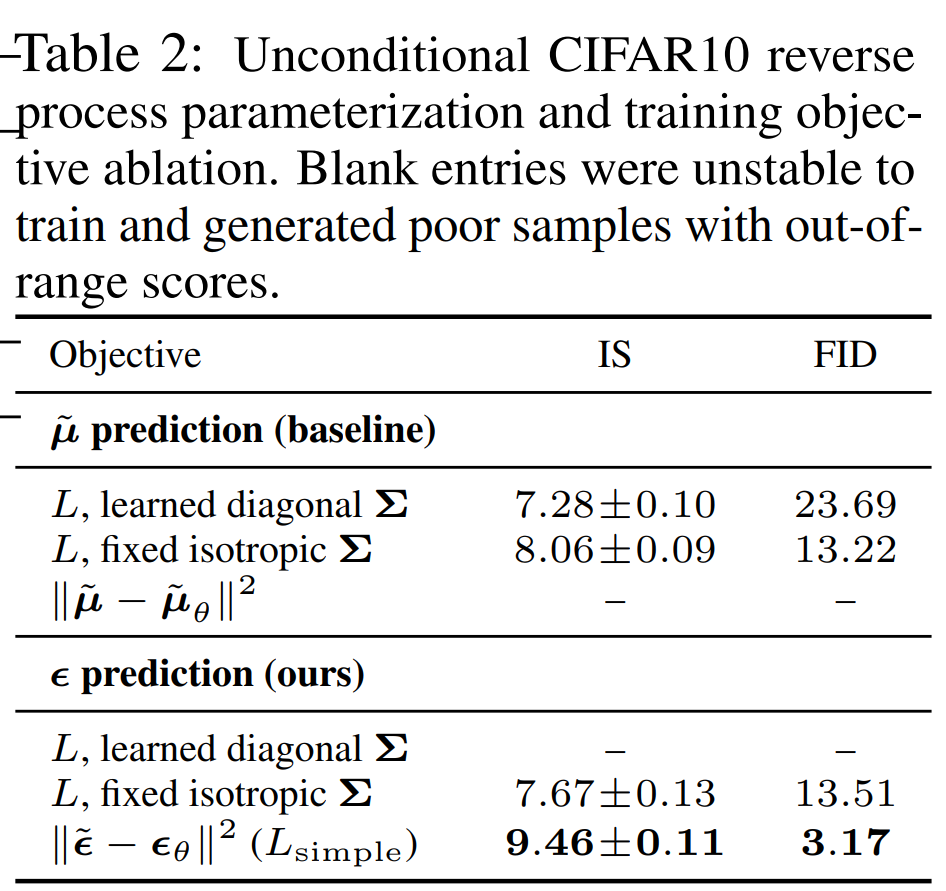
まず、\(\mu\)を予測した場合だと不安定だったため結果が記載されていません。
一方で \(\epsilon\) を予測した場合の一番単純化した \((17)\) 式を使った場合が一番精度が良くなっていることがわかります。
他にも \(\Sigma\) を学習させて場合もありますが、学習させない場合の方が結果が良くなっていることがわかります。
画像の生成過程
次に reverse process において生成される過程 \({\bf{x}}_t\) を見てみましょう。
以下のように、初めはランダムなノイズですが (一番左)、タイムステップが進むごとにだんだんとぼんやりした全体像が見えてきて、最後には詳細が鮮明になってきています。

潜在変数の共有
次に、同じ \({\bf{x}}_t\) から生成される画像を比較します。

Share x1000 とある一番左の4つの画像がありますが、これはその4つのうち右下の \({\bf{x}}_{1000}\) を共有して生成された画像です。
ですので、同じノイズから生成されているので、まったく違う画像が生成されています。
一方で Share x750 とある左から二番目の画像は同じ \({\bf{x}}_{750}\) から生成された画像です。
若干違うものの、すべてサングラスをかけているということが共通しています。
さらに500、250となるにつれ、同じような画像が生成されます。
潜在変数の補間
他にも以下のようにそれぞれのステップで潜在変数を画像を補間した場合に生成される画像を見ることができます。
ステップが1000に近いほどバラバラの画像になり、小さいステップで補間するほど具体的になり、あまり小さいステップだと無理やり補間してしまい、不自然な画像になってしまいます。

まとめ
今回は Diffusion モデルを見てきました。
まだ計算過程を記載しきれていない箇所や(解くのも大変ですが、式を書いていくのはさらに大変なので…)、確認しきれていないところがあるので、その辺りはおいおい記載していきたいと思います。
では、次は GLIDE や SR3 といった Diffusion モデルを見ていきたいと思います!!

