GELU(Gaussian Error Linear Units)は、OpenAI GPTやBERTで使われている活性化関数(activation)です。
BERTの論文で出てきても、「何かしらの活性化関数を使ってるんだなー」、とか「関数形だけ確認しておこう」となることが多いかもしれません。
それでも実務上は十分かもしれませんが、一度ぐらいは見ておいて損はないと思いますので、論文に沿って考え方や実験の結果を確認していきたいと思います。
https://arxiv.org/abs/1606.08415
GELUの関数形
結論から言うと、GELUの関数形は以下で定義されます。
$$\text{GELU}(x)=x\Phi(x)$$
\(\Phi(\cdot)\)は標準正規分布の分布関数です。
どうしてこうしたのか?は後でご紹介したいと思います。
また、誤差関数(\(\text{erf}(\cdot)\))を使って書くと、
$$ \text{GELU}(x)=x\cdot\frac{1}{2}\left[1+\text{erf}\left(x/\sqrt{2}\right)\right] $$
で表されます。
標準正規分布の分布関数や誤差関数は解析的に計算できないので、これを近似することにより、
$$\text{GELU}(x)\simeq 0.5x\left(1+\tanh\left[\sqrt{2/\pi}\left(x+0.044715x^3\right)\right]\right)$$
や
$$\text{GELU}(x)\simeq x\sigma(1.702x)$$
とすることも可能です。
\(\sigma(\cdot)\)はシグモイド関数です。
図で比較するとGELUは青線のような形で、ReLUが0以下で0を取り、0超で傾きが1になるのに対し、GELUはReLUを滑らかにしたような形になっています。
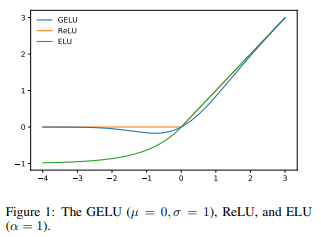
GELUの考え方
では、どうしてこのような関数形になったかを見ていきたいと思います。
大きな考え方としては、ReLU、ドロップアウト、ゾーンアウトの考え方を組み合わせたものです。
まずReLUですが、ReLUはインプットが0以上であれば1を掛けて、0未満であれば0を掛けたもので、以下のように表されます。
$$\text{ReLU}(x)=\max\{0, x\}=x{\bf{1}}_{x\ge 0}(x)$$
\({\bf{1}}_{x\ge 0}(\cdot)\)はindicator functionです。
つまり、ReLUはインプットの値によって確定的に0もしくは1を掛けるものです。
ドロップアウトはインプットの値には依らず、確率的にインプットにゼロを掛けるもの、ゾーンアウトはRNNにおいて確率的にインプットに1を掛けるようなものになります。
GELUではこれらの考え方を合わせて、インプットの値に応じて、確率的に0または1を掛けます。
そして、ドロップアウトでは一般にドロップアウト率というのを0.5や0.3などと決めて0を掛けますが、GeLUでは、インプットの値に依存するようにしたいので、その確率に正規分布の分布関数を使います。
つまり、\(\Phi(\cdot)\)を標準正規分布の分布関数とすると、\(\Phi(x)\)の確率でインプットに0を掛け(0にするのと同じ)、\(1-\Phi(x)\)の確率でインプットに1を掛けます。そして、その期待値をアウトプットにします。
したがって、GELUは
$$\text{GELU}(x)=\Phi(x)\times Ix + \left(1-\Phi(x)\right)\times0x=x\Phi(x)$$
と表されることになります。
少し「なるほど」という気がしますね。
これがGELUの考え方になり、ReLUに確率的な要素を持ち込むことにより、ReLUを滑らかにするという効果があります。
なお、必ずしも標準正規分布にする必要はなく、平均・分散をハイパーパラメータとすることも可能ですが、論文では標準正規分布を使用しています。
実験
ここでは、ReLU、ELUとGELUで収束の違いについて見ていきます。
論文では、色々なデータセットで試していますが、MNISTデータセットを使った結果のみをご紹介させていただきます。
ちなみに、ELUは、以下のような関数形で、\(\alpha\)はパラメータになりますが、\(\alpha=1\)としています。
$$\begin{align}
\text{ELU}(x) = \left\{\begin{array}{ll}x&\text{if } x> 0\\ \alpha \left(\exp\left(x\right)-1\right)&\text{if } x\le 0 \end{array}\right.
\end{align}$$
MNISTデータセットの結果
こちらが、MNISTデータセットで画像を分類した場合です。
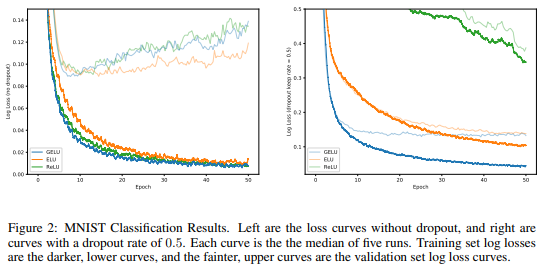
左がドロップアウトなし、右がドロップアウトありです。そして、濃い線が学習データセットで、青線がGELUです。
ドロップアウトなしの場合(左図)
学習データセットの結果(濃い線)を見ると、GELUが一番速く学習が進んでいることがわかります。その次にReLUが速いですね。
テストデータ(薄い線)については、一見、ん?となってしまいますが、すべてオーバーフィッティングしており、学習が速い分、GELUとReLUが早くオーバーフィッティングしてきています。
ただ、7~8エポックぐらいでおけるGELUの結果が一番ロスが小さくなっています。
ドロップアウトありの場合(右図)
テストデータセットで見ても圧倒的にGELUが早く収束しています。
GELUだと20エポックぐらいまででテストデータセットのlossは収束していますが、ELUでは同等のlossになるのに40から50エポックかかっており、2倍以上の収束スピードとなります。
これは大きいですね。
また、インプットにノイズを加えてノイズに対する頑健性を確認しています。
以下の通り、ノイズを大きくしていっても、GELUは相対的にテストデータセットのlossの増加が小さくなっていることがわかります。
つまり、ノイズに対して頑健であることが示唆されています。
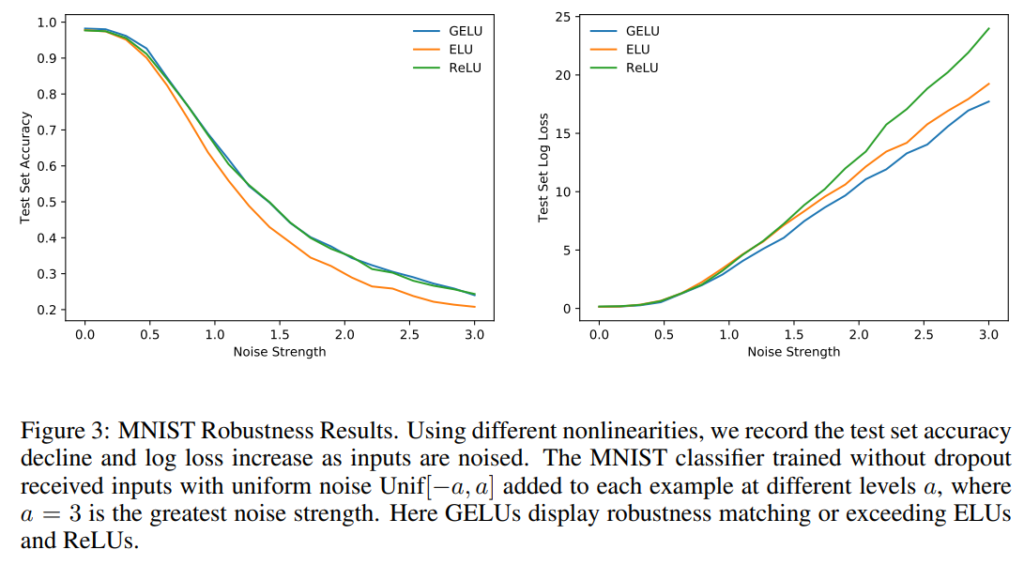
もう少し深く見てみましょう
GELUとReLU、ELUの関係
基本的に論文では標準正規分布を使ってGELUを定義していましたが、別に標準正規分布である必要はありません。
GELUで使う分布を平均0、分散が\(\sigma^2\)の正規分布としたとしましょう。
これを\(\text{GELU} _{\sigma^2}(x) \)と表します。
そして、このGELUで\(\sigma^2\)をゼロに近づけていくととReLUと一致します。
なぜなら、\(\sigma^2\)をゼロに近づけていくと以下のように、\(\mu=0\)の正規分布は0以上で1、0未満で0を取るindicator function \({\bf{1}}_{x>0}(x)\)に近づいていき、\(x\Phi_{\mu=0, \sigma^2}(x)\)がReLUの定義である\(x{\bf{1}}_{x\ge 0}(x)\)に近づくからです。
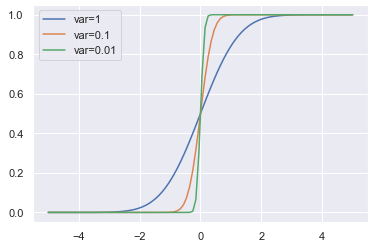
ELUの関係については、\(\alpha=1/\pi\)のときにELUでは、負の領域で\(xP(C\le x), C~\text{Cauchy}(0, 1)\)と標準コーシー分布に漸近し、正の領域で\(1/\pi\)だけ下にずらすと同様に\(xP(C\le x)\)に漸近するとのことです。
GELUとReLU、ELUの違い
一方で、GELUとReLU、ELUの大きな違いは、以下です。
- ReLU、ELUは正の領域で直線だが、GELUについては、正の領域でも曲率がある。
- GELUは単調増加ではない。
- GELUは確率的な要素を加味している。
これらの違いがよい影響を与えていると考えられます。
まとめ
ということで今回は、OpenAI GPTやBERTで使われている活性化関数GELUについてざっと見てきました。
何となく使っていることが多いかもしれませんが、よく見ると定式化に当たって色々考慮されていたようですね。
他にも実験結果はありますが概ね同様の結果ですので、ご興味のある方は論文を読んでいただければと思います。
OpenAI GPTやBERTについてはこちらをご参照ください。

