条件付き確率場(Conditional Random Fields; CRF)を使った品詞タグ付け

今回は“条件付き確率場(Conditional Random Fields; CRF)”を使った品詞タグ付けについて解説したいと思います。

条件付き確率場は、例えば単語列xが与えられたときに、品詞ラベル列yなどの系列を予測するためのモデルです。

MeCabでは形態素解析にこのCRFを使っており、固有表現抽出でもよく使われている手法ですので、式変形は多少ややこしい部分もありますが、是非一度目を通していただければと思います。

今回は主に以下の本を参考にしています。
数式をしっかりと書いているので、数式が苦手でない人にはオススメです。

リンク

1 条件付き確率場(Conditional Random Fileds; CRF)とは
2 ラベルの推定
3 条件付き確率場の学習
4 前向き後ろ向きアルゴリズム
5 パラメータの更新
6 アンダーフローの問題
7 まとめ
- 7.1 参考文献

条件付き確率場(Conditional Random Fileds; CRF)とは

条件付き確率場は、入力${\bf{x}}$に対して品詞ラベルの系列${\bf{y}}$が出力される条件付き確率$P({\bf{y}}|{\bf{x}})$を計算するモデルです。

そして、その条件付き確率が以下のように与えられます(対数線形モデル)。

$$\begin{align}
P({\bf{y}}|{\bf{x}})&=\frac{\exp(h({\bf{x}}, {\bf{y}}))}{Z}\\
&=\frac{\exp({\bf{w}}\cdot\phi({\bf{x}}, {\bf{y}}))}{Z}\\
\end{align}$$

${\bf{w}}$は$K$次元のパラメータ・ベクトルです。

また、$\phi(\cdot)$は素性関数と呼ばれるもので、例えば$k$番目の素性を

$$\begin{align}
\phi_k({\bf{x}},{\bf{y}})=\left\{\begin{array}{ll}1&t-1\text{番目の品詞が名詞かつ}t\text{番目の品詞が動詞} \\ 0&\text{それ以外}\end{array} \right.
\end{align}$$

というように0または1で表現します。

この素性関数は目的に合うようにモデル構築時に設計します。

そして、そういった素性を$K$個並べた$K$次元のベクトルが$\phi({\bf{x}}, {\bf{y}})\in \mathbb{R}^K$です。

$Z$は$\sum_{{\bf{y}}\in \mathcal{Y}({\bf{x}})}P({\bf{y}}|{\bf{x}})=1$となるようにする正規化項で、

$$Z:=\sum_{{\bf{y}}\in\mathcal{Y}({\bf{x}})}\exp({\bf{w}}\cdot\phi({\bf{x}}, {\bf{y}}))$$

です。

ディープラーニングなどでよく出てくるsoftmax関数を思い浮かべればよいかもしれません。

なお、${\bf{y}}\in \mathcal{Y}({\bf{x}})$は、入力単語列${\bf{x}}$に対して与えられる品詞ラベル列のすべての組合せ(厳密には順列)を表します。

条件付き確率場の仮定

条件付き確率場では、これを単純化して1階のマルコフ性と素性関数の線形性を仮定します。

これにより計算を高速化することが可能です。

すなわち、

$$\begin{align}
\phi({\bf{x}}, {\bf{y}})=\sum_{t}\phi_t({\bf{x}}, y_{t-1}, y_t)
\end{align}$$

とすることにより、条件付き確率を

$$\begin{align}
P({\bf{y}}|{\bf{x}})=\frac{\exp(\sum_{t}{\bf{w}}\cdot\phi_t({\bf{x}}, y_{t-1}, y_t))}{Z}\\
\end{align}$$

で表します。

つまり、$t$番目の素性はインプットとなる単語全体と$t$番目、$t-1$番目のラベルだけで決まり、それの和を素性とするというものです。

ですので、$t$番目のラベルは$t-2$番目以前の単語のラベルとは無関係であるという仮定を置いており、その仮定を満たすような素性を設計しなければなりません。

モデルは以上になります。

ラベルの推定

まずは、パラメータ${\bf{w}}$がわかっているとして、最適なラベルの推定方法を見ていきます。

最適なラベル列は、

$$\begin{align}
\widehat{{\bf{y}}} &= \arg\max_{\bf{y}} P({\bf{y}}|{\bf{x}})\\
&=\arg\max_{\bf{y}} \frac{\exp({\bf{w}}\cdot\phi({\bf{x}}, {\bf{y}}))}{Z}\\
&=\arg\max_{\bf{y}} {\bf{w}}\cdot\phi({\bf{x}}, {\bf{y}})\\
&=\arg\max_{\bf{y}} \sum_{t} {\bf{w}}\cdot \phi_t({\bf{x}}, y_{t-1}, y_t)
\end{align}$$

で求めることができます。

つまり、$\sum_{t} {\bf{w}}\cdot \phi_t({\bf{x}}, y_{t-1}, y_t)$が最大になるようなラベル列${\bf{y}}$が最適なラベルの系列になります。

ここで重要なのは、上記の1階のマルコフ性と素性関数の線形性の仮定により、$\phi$が$y_t$と$y_{t-1}$にしか依存しなくなっているところです。

それにより、ビタビアルゴリズムを使うことによって、すべての${\bf{y}}$の組合せを計算するのではなく前から順番に計算するだけで済み、効率よく$\widehat{{\bf{y}}}$を求めることができます。

ビタビアルゴリズムについてはこちらの記事をご参照だくさい。

: 品詞タグ付け(part-of-speech tagging)を理解する - ビタビアルゴリズム
『品詞タグ付け(part-of-speech tagging)を理解する』では、隠れマルコフモデルを使って、単語列xが与えられたときに品詞ラベル列がyとなる確率の求め方を解説しました。まだ、このまま ...

条件付き確率場の学習

さきほどはパラメータベクトル${\bf{w}}$がわかっているものとしました。

ここでは、${\bf{w}}$の求め方、つまり条件付き確率場の学習方法を見ていきましょう。

考え方は非常にシンプルで、各サンプルの対数尤度を最大化します。

実際には、マイナスを付けたものを最小化するという問題に置き換えます。

$i$番目のサンプルの対数尤度(にマイナスを付けたもの)は、

$$\begin{align}
\mathcal{L}_i({\bf{w}}|{\bf{x}}^{(i)}, {\bf{y}}^{(i)}) &= -\log P({\bf{y}}^{(i)}|{\bf{x}}^{(i)})\\
&= -{\bf{w}}\cdot\phi({\bf{x}}^{(i)}, {\bf{y}}^{(i)}) + \log(Z)
\end{align}$$

と表されます。

$N$を学習サンプル数とすると、全体の目的関数は、

$$\mathcal{L}({\bf{w}}|{\bf{x}}, {\bf{y}})=\sum_{i=1}^{N}\mathcal{L}_i({\bf{w}}|{\bf{x}}^{(i)}, {\bf{y}}^{(i)})$$

で計算できます。

この目的関数を最小化するためには勾配が必要ですが、この時のサンプル$i$から計算される勾配は、

$$\begin{align}
\frac{\partial \mathcal{L}_i}{\partial {\bf{w}}} &= -\phi({\bf{x}}^{(i)}, {\bf{y}}^{(i)}) + \sum_{{\bf{y}}\in\mathcal{Y}({\bf{x}}_i)} \phi({\bf{x}}, {\bf{y}})P({\bf{y}}|{\bf{x}})
\end{align}$$

になります。全体の目的関数に対する勾配は各サンプルの勾配の和を取ればよいだけです。

ここで、1項目は問題ありませんが、2項目はすべての${\bf{y}}$の組合せについて計算しなければなりません。

そこで、少し変形して(ここから$i$の添え字は省略します)、

$$\begin{align}
\sum_{{\bf{y}}\in\mathcal{Y}({\bf{x}})} \phi({\bf{x}}, {\bf{y}})P({\bf{y}}|{\bf{x}})&=\sum_{{\bf{y}}\in\mathcal{Y}({\bf{x}})} \sum_{t=1}^{T+1}\phi_t({\bf{x}}, y_t, y_{t-1})P({\bf{y}}|{\bf{x}})\\
&=\sum_{{\bf{y}}\in\mathcal{Y}({\bf{x}})}\phi_1({\bf{x}}, y_1, y_0)P({\bf{y}}|{\bf{x}}) +\cdots + \sum_{{\bf{y}}\in\mathcal{Y}({\bf{x}})}\phi_{T+1}({\bf{x}}, y_{T+1}, y_T)P({\bf{y}}|{\bf{x}}) \\
&=\sum_{y_1,y_0}\phi_1({\bf{x}}, y_1, y_0)P(y_1, y_0|{\bf{x}}) +\cdots \\
&+ \sum_{y_{T+1}, y_T}\phi_{T+1}({\bf{x}}, y_{T+1}, y_T)P(y_{T+1}, y_T|{\bf{x}}) \\
&= \sum_{t=1}^{T+1}\sum_{y_t, y_{t-1}}P(y_{t}, y_{t-1})\phi_t({\bf{x}}, y_t, y_{t-1})
\end{align}$$

と表します。

ここで、単語列${\bf{x}}$は長さ$T$とし、$t=0$というのはBOS、$t=T+1$はEOSに対応する単語の位置を表すものとします。

つまり、$y_0=\text{BOS}$、$y_{T+1}=\text{EOS}$となります。

また、$\sum_{y_t, y_{t-1}}$は$y_t$と$y_{t-1}$に関して、すべての取り得る組合せの和を取ることを意味しています。

これにより、各$t$について$\sum_{y_t, y_{t-1}}P(y_{t}, y_{t-1})\phi_t({\bf{x}}, y_t, y_{t-1})$を計算していけばよいことになります。

あとは、$P(y_t, y_{t-1})$を効率よく計算できればよいのですが、ここで、動的計画法の一種である前向き後ろ向きアルゴリズム(Baum-welch algorithm)を用いて効率よく計算する方法をご紹介します。

前向き後ろ向きアルゴリズム

まず、表記を簡単にするために

$$\psi_t(y_t, y_{t-1}):=\exp({\bf{w}}\cdot\phi_t({\bf{x}}, y_t, y_{t-1}))$$

とします。

すると、

$$\begin{align}
P({\bf{y}}|{\bf{x}})&=\frac{\exp({\bf{w}}\cdot\phi({\bf{x}}, {\bf{y}}))}{Z}\\
&=\frac{\exp({\bf{w}}\cdot\prod_{t=1}^{T+1}\phi_t({\bf{x}}, y_{t}, y_{t-1}))}{Z}\\
&=\frac{1}{Z}\prod_{t=1}^{T+1}\psi_t(y_t, y_{t-1})
\end{align}$$

と表されます。

ここから$P(y_t, y_{t-1}|{\bf{x}})$を計算します。

$P(y_t, y_{t-1}|{\bf{x}})$は周辺確率になるので、$y_t$、$y_{t-1}$以外の組合せで確率を合計することにより求めることが可能です。

$$\begin{align}
P(y_t, y_{t-1}|{\bf{x}})&=\sum_{{\bf{y}}_{0:t-2}}\sum_{{\bf{y}}_{t+1:T+1}}P({\bf{y}}|{\bf{x}})
\end{align}$$

$\sum_{{\bf{y}}_{0:t-2}}$は0番目から$t-2$番目までのラベルをすべての組み合わせについて合計するということで、$\sum_{{\bf{y}}_{t+1:T+1}}$は$t+1$番目から$T+1$番目までのラベルをすべての組み合わせについて合計するということです。

もう少し変形すると、

$$\begin{align}
P(y_t, y_{t-1}|{\bf{x}})&=\sum_{{\bf{y}}_{0:t-2}}\sum_{{\bf{y}}_{t+1:T+1}}P({\bf{y}}|{\bf{x}})\\
&=\frac{1}{Z}\sum_{{\bf{y}}_{0:t-2}}\sum_{{\bf{y}}_{t+1:T+1}}\prod_{t'=1}^{T+1}\psi_t(y_{t'}, y_{t'-1})\\
&=\frac{\psi(y_{t}, y_{t-1})}{Z}\sum_{{\bf{y}}_{0:t-2}}\sum_{{\bf{y}}_{t+1:T+1}}\prod_{t'=1}^{T+1,t'\neq t}\psi_t(y_{t'}, y_{t'-1})\\
&=\frac{\psi(y_{t}, y_{t-1})}{Z}\left(\sum_{{\bf{y}}_{0:t-2}}\prod_{t'=1}^{t-1}\psi_t(y_{t'}, y_{t'-1})\right)\left(\sum_{{\bf{y}}_{t+1:T+1}}\prod_{t'=t+1}^{T+1}\psi_t(y_{t'}, y_{t'-1})\right)\\
\end{align}$$

と変形できます。

1行目から2行目は、単純に$\psi_t(y_{t}, y_{t-1})$をくくりだしただけで、2行目から3行目は$\prod_{t'=1}^{T+1,t'\neq t}\psi(y_{t'}, y_{t'-1})$の部分を2つに分けています。

そして、

$$\begin{align}
\alpha(y_t, t)&:=\sum_{{\bf{y}}_{0:t-1}}\prod_{t'=1}^{t}\psi_t(y_{t'}, y_{t'-1})\\
\beta(y_t, t)&:=\sum_{{\bf{y}}_{t+1:T+1}}\prod_{t'=t+1}^{T+1}\psi_t(y_{t'}, y_{t'-1})
\end{align}$$

と置くと、

$$\begin{align}
P(y_t, y_{t-1}|{\bf{x}})&=\frac{\psi_t(y_t, y_{t-1})}{Z}\alpha(y_{t-1}, t-1)\beta(y_t, t)
\end{align}$$

と表されます。

あとは、$\alpha$、$\beta$、$Z$を高速に計算できればよいので、これらを効率的に計算していく方法を見ていきます。

前向きアルゴリズム

まずは、$\alpha$の計算方法です。

もとのままだと、$\alpha(y_{t}, t)$は0から$t-1$までのラベルについて、すべての組み合わせを考慮しなくてはいけません。

単語数、品詞ラベル数が増えると指数的に計算量が増えてしまいますので、ビタビアルゴリズムのように毎回いちから計算するのではなく、途中までの計算結果を使って計算します。

具体的には、

$$\begin{align}
\alpha(y_t, t)&=\sum_{{\bf{y}}_{0:t-1}}\prod_{t'=1}^{t}\psi_{t'}(y_{t'}, y_{t'-1})\\
&=\sum_{{\bf{y}}_{0:t-1}}\left[\psi_{t}(y_{t}, y_{t-1})\prod_{t'=1}^{t-1}\psi_{t'}(y_{t'}, y_{t'-1})\right]\\
&=\sum_{y_{t-1}}\left[\psi_{t}(y_{t}, y_{t-1})\sum_{{\bf{y}}_{0:t-2}}\prod_{t'=1}^{t-1}\psi_{t'}(y_{t'}, y_{t'-1})\right]\\
&=\sum_{y_{t-1}}\psi_{t}(y_{t}, y_{t-1})\alpha(y_{t-1}, t-1)
\end{align}$$

と変形できます。

ここで、$\alpha(y_0, 0)=1$とします。

つまり、$\alpha(y_{t-1}, t-1)$がわかっているとすると、いちから$\alpha(y_t, t)$を計算しなくても、$\alpha(y_{t-1}, t-1)$を使って計算することができ、いちからすべての${\bf{y}}$の組み合わせを計算する必要がないということです。

イメージ図は以下のようになります。

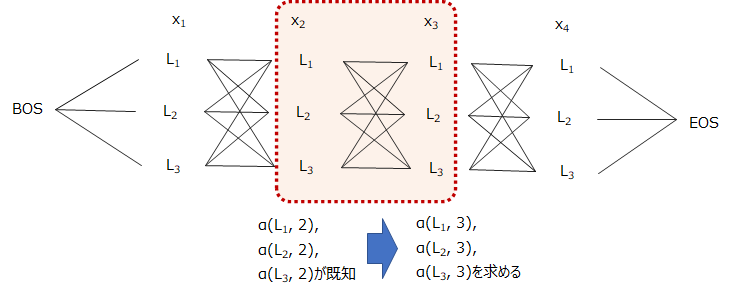
前から順番に後ろに向かって計算していき、最後にEOSまで行きつくので、前向きアルゴリズムと呼びます。

後ろ向きアルゴリズム

次は、$\beta(y_t, t)$についても同じように変形していきます。

$$\begin{align}
\beta(y_t, t)&=\sum_{{\bf{y}}_{t+1:T+1}}\prod_{t'=t+1}^{T+1}\psi_{t'}(y_{t'}, y_{t'-1})\\
&=\sum_{{\bf{y}}_{t+1:T+1}}\left[\psi_{t+1}(y_{t+1}, y_{t})\prod_{t'=t+2}^{T+1}\psi_{t'}(y_{t'}, y_{t'-1})\right]\\
&=\sum_{y_{t+1}}\left[\psi_{t+1}(y_{t+1}, y_{t})\sum_{{\bf{y}}_{t+2:T+1}}\prod_{t'=t+2}^{T+1}\psi_{t'}(y_{t'}, y_{t'-1})\right]\\
&=\sum_{y_{t+1}}\psi_{t+1}(y_{t+1}, y_{t})\beta(y_{t+1}, t+1)
\end{align}$$

となります。

$\beta(y_{T+1}, T+1))=1$とします。

イメージ図は以下のようになります。

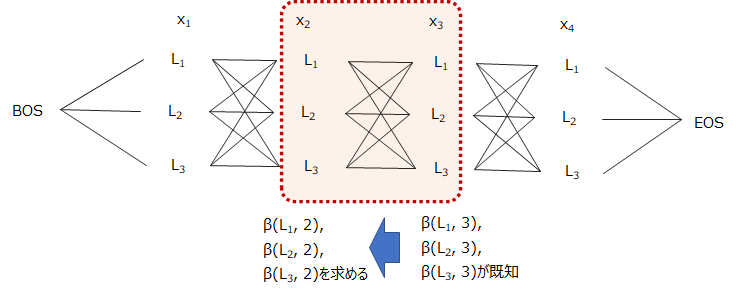
後ろから前に向かって順番に計算していき、最後にBOSに行きつくので、後ろ向きアルゴリズムと呼ばれます。

$Z$の計算

これは単純に

$$Z=\alpha(y_{T+1}, T)$$

で計算することができます。

パラメータの更新

以上で、$P(y_t,y_{t-1}|{\bf{x}})$を計算するためのパーツがそろいました。

これで勾配を求めることができますので、あとは勾配をもとにパラメータを更新します。

パラメータの更新は、

$${\bf{w}}' = {\bf{w}} - \eta \frac{\partial\mathcal{L}}{\partial{\bf{w}}}$$

で行います。

$\eta$はあらかじめ設定する学習率になります。

アンダーフローの問題

ただこのままでは、$\alpha$、$\beta$の計算で、積が繰り返されていくことから、オーバーフロー・アンダーフローが発生します。

そこで、ひとつの対応方法は、対数を取ることです。

$\alpha$、$\beta$ではなく、$\widetilde{\alpha}=\log(\alpha)$、$\widetilde{\beta}=\log(\beta)$を計算することで、

$$\begin{align}
\log(\alpha(y_t, t))&=\log(\sum_{y_{t-1}}\psi_t(y_t, y_{t-1})\alpha(y_{t-1}, t-1))\\
&=\log(\sum_{y_{t-1}}\psi_t(y_t, y_{t-1})\exp(\log(\alpha(y_{t-1}, t-1))))
\end{align}$$

から、

$$\begin{align}
\widetilde{\alpha}(y_t, t))&=\log(\sum_{y_{t-1}}\psi_t(y_t, y_{t-1})\exp(\widetilde{\alpha}(y_{t-1}, t-1))))
\end{align}$$

となります。

同様に$\log(\beta)$についても、

$$\begin{align}
\widetilde{\beta}(y_t, t))&=\log(\sum_{y_{t+1}}\psi_t(y_t, y_{t+1})\exp(\widetilde{\beta}(y_{t+1}, t+1))))
\end{align}$$

と表されます。

さらに、$\log(\sum_i\exp(x_i))$という形はlogsumexpという計算手法を適用することで、アンダーフローが起こらないようにうまく計算することができます。

こちらの詳細はここでは省略しますが、興味ある方はインターネットや下記の参考文献にも載っていますので調べてみてください。