今回は、文章生成やSeq2Seqモデルを使った機械翻訳などでよく使われるビームサーチ(Beam Search)について解説したいと思います。
より理解しやすくするために、以下の3つを手法を順番に説明していきます。
- Greedy Search(貪欲法)
- Exhaustive Search(しらみつぶし探索)
- Beam Search(ビームサーチ)
まず、以下はLSTMを使った文章生成の例です。

文章生成においては、このようにそれまでの出力した単語をもとに次の単語を順番に予測していきます。
具体的には、\(t\)時点の単語\(y_t\)を予測するのに、それまでの単語\(y_1, y_2, \cdots, y_{t-1}\)とコンテキスト・ベクトル\({\bf{c}}\)を使って予測します。
この際に、ボキャブラリー\(\mathcal{V}\)から1つ単語を選ぶという作業を行います。
そして、<EOS>というダミーの単語が選択されたら、そこで文章生成が終了となります。
文章中の単語数が\(T\)であれば、ボキャブラリー数を\(|\mathcal{V}|\)で表すと、本来単語の列の候補は\(|\mathcal{V}|^T\)通りあり、そこから1つのパターンを抜き出すという作業になります。
例えば、ボキャブラリー数が10個という非常に少ない場合でも、10単語の文章を生成すると、その候補は1010通りなので100億通りの組み合わせがあります。
そして、実際のボキャブラリー数は数万といったオーダーになることが多いです。
どのような観点で多数の組合せの中から一つの文章を選ぶかというと、コンテキストベクトルで条件づけて、もっとも確率が高くなるような単語列を出力します。
式で表すと、
$$\begin{align}
p(y_1, \cdots, y_T|{\bf{c}})=\prod^T_{t=1}P(y_t|y_1, y_{t-1}, {\bf{c}})
\end{align}$$
を最大化するような単語列\({\bf{y}}\)を求める必要があります。
上式の求め方の代表例が上記の3つの方法です。
それではこの3つの方法を順番に見ていきましょう。
Greedy Search(貪欲法)
では、上記の1つのパターンを抜き出す方法の1つ目です。
Greedy Searchでは、\(t\)番目の単語は、条件付き確率がもっとも高くなるような単語を選びます。
$$y_t = \arg\max_{y\in\mathcal{V}} P(y_t|y_1,\cdots, y_{t-1},c)$$
t=1から順番にこの条件付き確率が高くなる単語を選んでいき、<EOS>が選ばれた時点で文章生成を終了します。
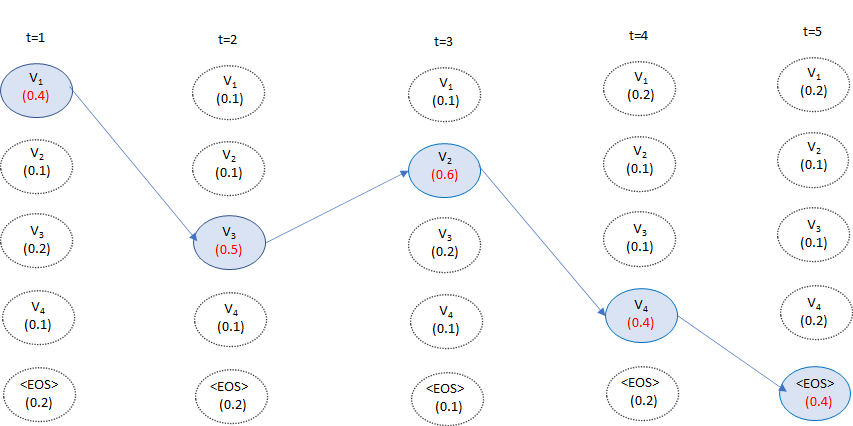
ここで注意したいのは、あくまで各時点で最適な単語を選んできているのですが、必ずしも文章として最適であるというわけではない、ということです。
イメージとしては、各周辺確率が最大になるように選んできていることになります。
ただし、計算量は小さく\(|\mathcal{V}|\)個の中から1つ選ぶ作業を\(T\)回行うので、\(O(|\mathcal{V}|\times T)\)となります。
Exhaustive Search(しらみつぶし探索)
Exhaustive Searchでは、すべてのパターンを計算して最良の単語列を求めます。
つまり、直接
$$\begin{align}
\arg\max_{y_1, \cdots, y_T}p(y_1, \cdots, y_T|{\bf{c}})
\end{align}$$
を求めていることになります。
この方法は正確ですが、計算量が\(O(|\mathcal{V}|^T)\)となるので、非常に計算量が多くなります。
単語数が10,000個とかある中で、20単語の文章を生成するだけでも、10,00020通りを計算しないといけないので、現実的ではありません。
Beam Search(ビームサーチ)
では、本題のBeam Searchです。
こちらは、Greedy SearchとExhaustive Searchの中間のようなもので、正確性と計算量のトレードオフを考慮した方法です。
Greedy Searchは、各時点で1つ候補となる単語を選んでいましたが、Beam Searchでは候補となる単語を複数選びます。
この候補数をビームサイズと言い、\(k\)で表します。
つまり、\(k\)を1にした場合がGreedy Searchで、\(k\)をボキャブラリー全体の数にした場合がExhaustive Searchになります。
ですので、計算量は\(O(k\times |\mathcal{V}| \times T)\)となり、Greedy Searchよりは\(k\)倍計算量が多くなりますが、Exhaustive Searchよりははるかに計算量を減らすことが可能です。
具体的な方法
では、具体的な方法を説明します。
まず、一つ目の単語をモデルが予測する確率にもとづいて選びます。
Greedy Searchでは一つでしたが、Beam Searchではビームサイズの\(k\)個を選びます。
ですので、予測確率(スコア)が高い上位\(k\)個を選びます。
例としてボキャブラリー数が5、ビームサイズが3の場合を考えてみましょう。
LSTMなどのモデルが出力するt=1における予測確率が高いV1、V3、V5を選びます。

Greedy Searchでは、この時点で1つだけが選ばれており、Exhaustive Searchでは5個が選ばれていることになります。
次に、t=2においてt=1がV1、V3、V5のときの条件付き確率\(P(y|y_1=V_1, {\bf{c}})\)、\(P(y|y_1=V_3, {\bf{c}})\)、\(P(y|y_1=V_5, {\bf{c}})\)をそれぞれ計算します。
ボキャブラリー数は5ですので、5×3の15通りを計算します。
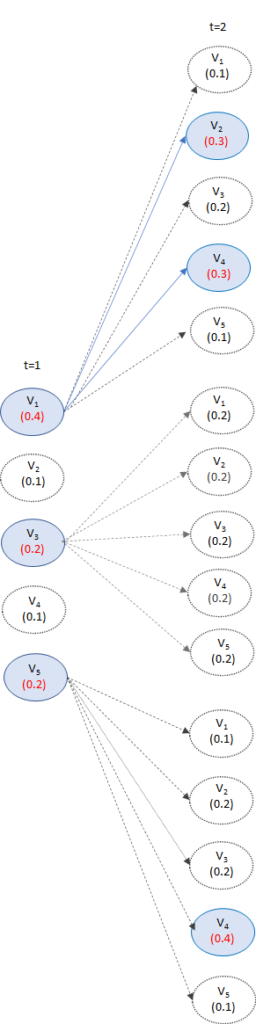
そしてその中で、その中でスコアが高い3パターンを選びます。
もしかすると、上の図のように、t=1についてはV3のパターンが消え、V1とV5のみのパターンが残ることもあります。
同様にt=3でも、t=2で残った候補から続く最適な単語列を3つ選びます。
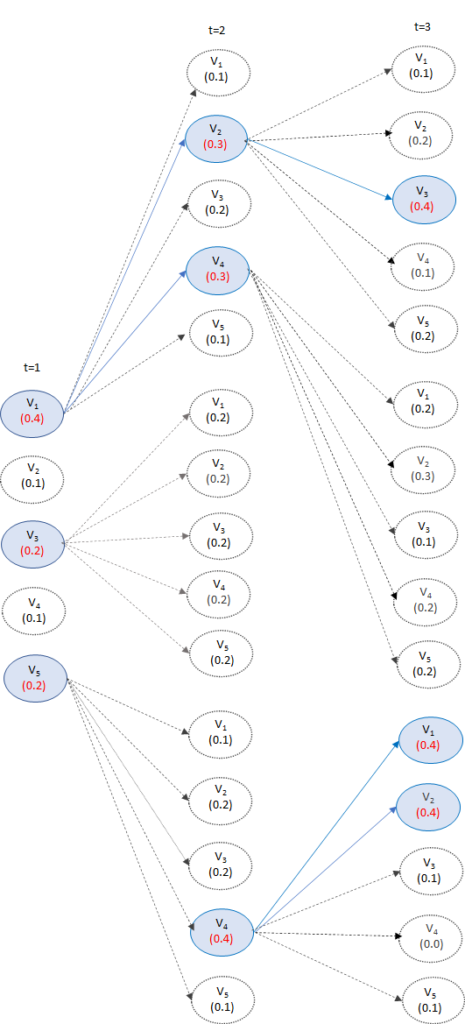
そして、これを繰り返して<eos>が選ばれるまで続けます。
これにより、どの時点でも常にビームサイズ分の候補だけが残っている状態になり、妥当な文章だけを残しながら、計算量を減らすことができます。
以上が、Beam Searchの説明になります。
まとめ
今回はBeam Searchについて解説しました。
時点時点で最適なものを選ぶGreedy Searchとすべての組合せを計算して最良の系列を選ぶExhaustive Searchの間で、計算量を現実的なレベルにしながら、より良い文章を生成するためのものです。
皆さんもLSTMやTransformerなどを使って文章生成用のアルゴリズムを作成した際は、Beam Searchも最後に組み込んで、より良い文章を作成してみては如何でしょうか。
では、また!