さて今回は、いつもと趣向を変えて、COVID-19のデータを使って、Plotlyで可視化・分析をしてみたいと思います。
ただ、分析を深くやるというよりは、Plotlyを使ってどのように分析するか、どのようなグラフを作成するか、という内容がメインです。
ですので、予測するために人流データなどの特徴量は使っていません。
もしCOVID-19やその予測について興味がある方は他のサイトをご参照ください。
モチベーションとしては、最近(2021年7月)はコロナの新規陽性者数が多いものの、高齢者のワクチン接種が進んでいるので、重傷者数が増えないのかなと思いますが(皆様もそうかと思いますが)、それを確認したいというものです。
ですので、現時点における陽性者数と重傷者数の関係を理解し、今後の重傷者の推移を理解する上で参考にしたいと思い、軽く分析してみました。
もちろん色々思いはありますが、コロナ対策がどうとか、東京の人口を考えたらとか、政治的な話は一切しませんし、個人的な意見は出しませんので、あくまで数値を見ていくというものです。
plotlyを使った分析
とりあえず、東京都のHPから陽性者数と重傷者数を取ってきて、データフレームを作成しました。
まずは必要なパッケージをインポートします。
import plotly.graph_objects as go import plotly.express as px from plotly.subplots import make_subplots import pandas as pd import datetime
データはこのようになっています。
| 日付 | 陽性者数 | 入院患者数 | 重症者数 |
|---|---|---|---|
| 2020-01-20 | 0 | NaN | NaN |
| 2020-01-21 | 0 | NaN | NaN |
| 2020-01-22 | 0 | NaN | NaN |
| 2020-01-23 | 0 | NaN | NaN |
| 2020-01-24 | 1 | NaN | NaN |
| ... | ... | ... | ... |
| 2021-07-04 | 518 | 1640.0 | 51.0 |
| 2021-07-05 | 342 | 1674.0 | 57.0 |
| 2021-07-06 | 593 | 1677.0 | 63.0 |
| 2021-07-07 | 920 | 1673.0 | 62.0 |
| 2021-07-08 | 896 | 1782.0 | 60.0 |
データを眺める
では、とりあえず、陽性者数と重傷者数を重ねてプロットしてみましょう。
2軸のプロットを使います。
fig = go.Figure()
fig.add_trace(go.Scatter(x=df['日付'],
y=df['陽性者数'],
name='陽性者数',
yaxis='y')
)
fig.add_trace(go.Scatter(x=df['日付'],
y=df['重症者数'],
name='重症者数',
yaxis='y2')
)
fig.update_layout(yaxis1=dict(side='left'),
yaxis2=dict(side='right',
overlaying='y',
showgrid=False))
重ねてプロットしたのは、陽性者数と重傷者数の推移のラグなどを見たかったからです。
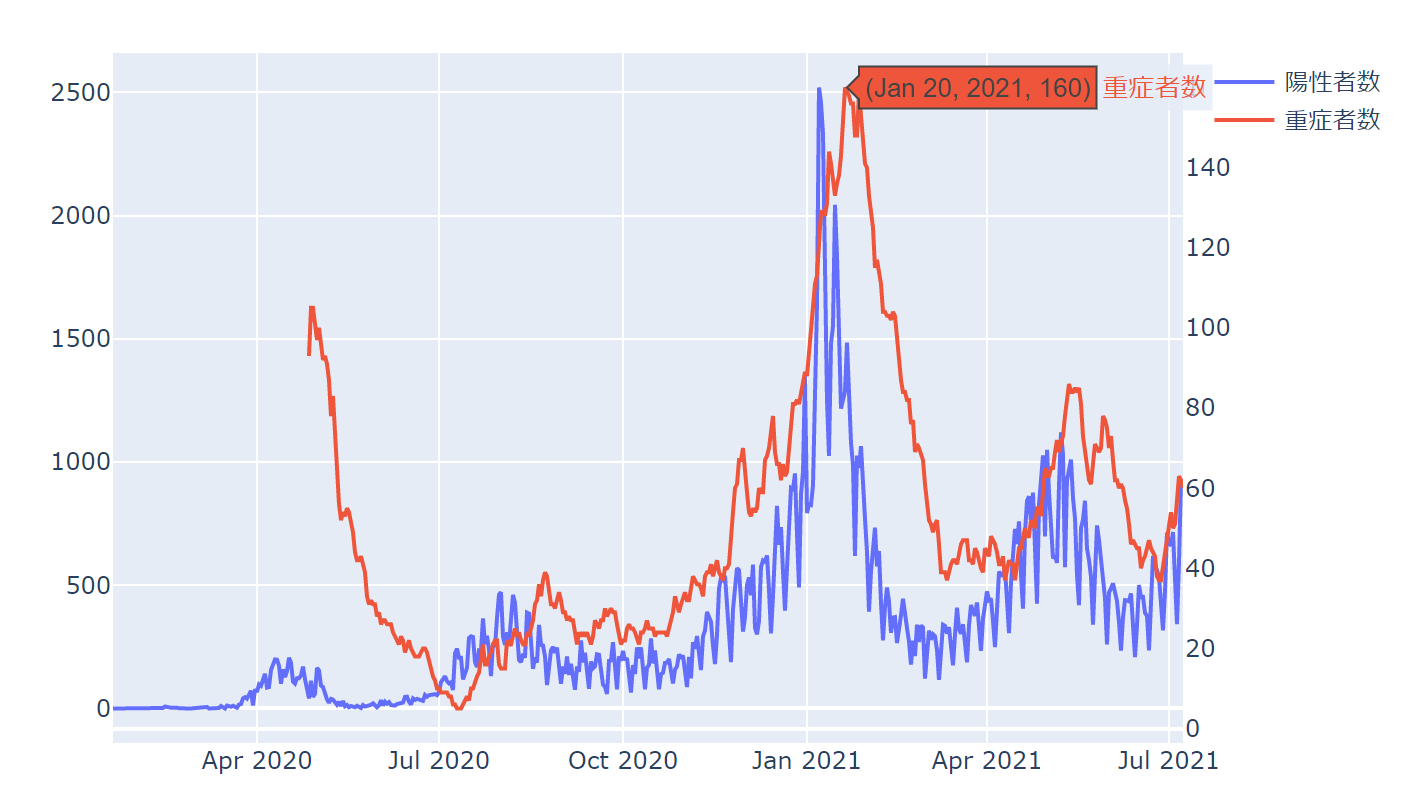
この段階では、まだ見やすくしたりといったことはせず、雑にグラフを作成してデータを確認します。
plotlyのようなインタラクティブなグラフを使ういいところは、カーソルを当てたときに数値などの詳細情報を見ることができるところです。
2021年1月20日に重症者数が160人で重症者数のピークになっています。
では、このグラフを人に見せる場合はどうしましょう。
例えば、無駄なグリッド線などを取り除き、参考となる緊急事態宣言の期間を入れ、カーソルを当てたときのテキストを整えます。
各線の説明については凡例ではなく、直接グラフに「陽性者数」、「重傷者数」と記載するようにします。
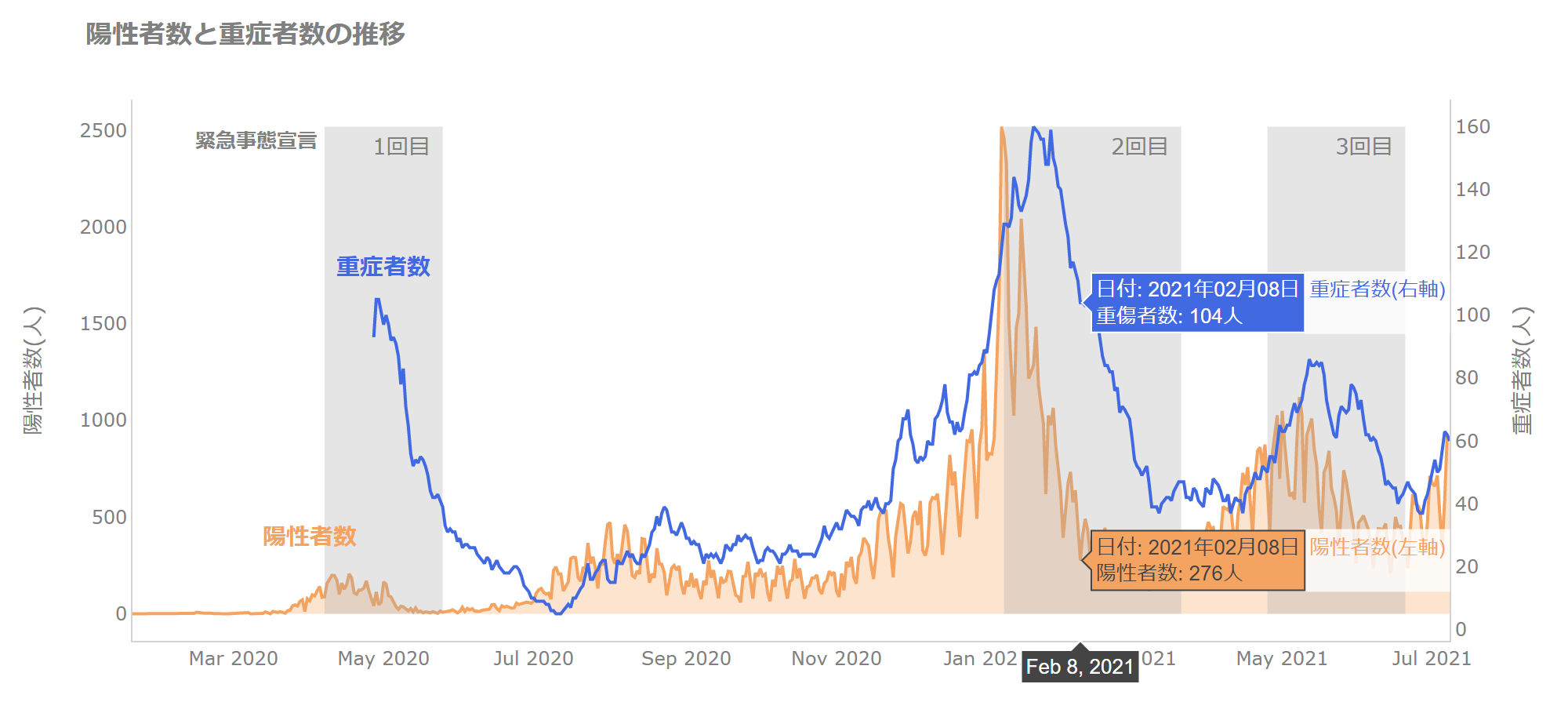
緊急事態宣言により新規陽性者数、重傷者数が減っていくのがわかります。
ただし、報道でもあるように宣言期間の後半については下げ止まるようですね。
ちなみに、凡例にすると下図のようになりますが、2軸のグラフを使っているということもあり、色んなところに目をやる必要があって、認知負荷が高くなるのがわかりますね。
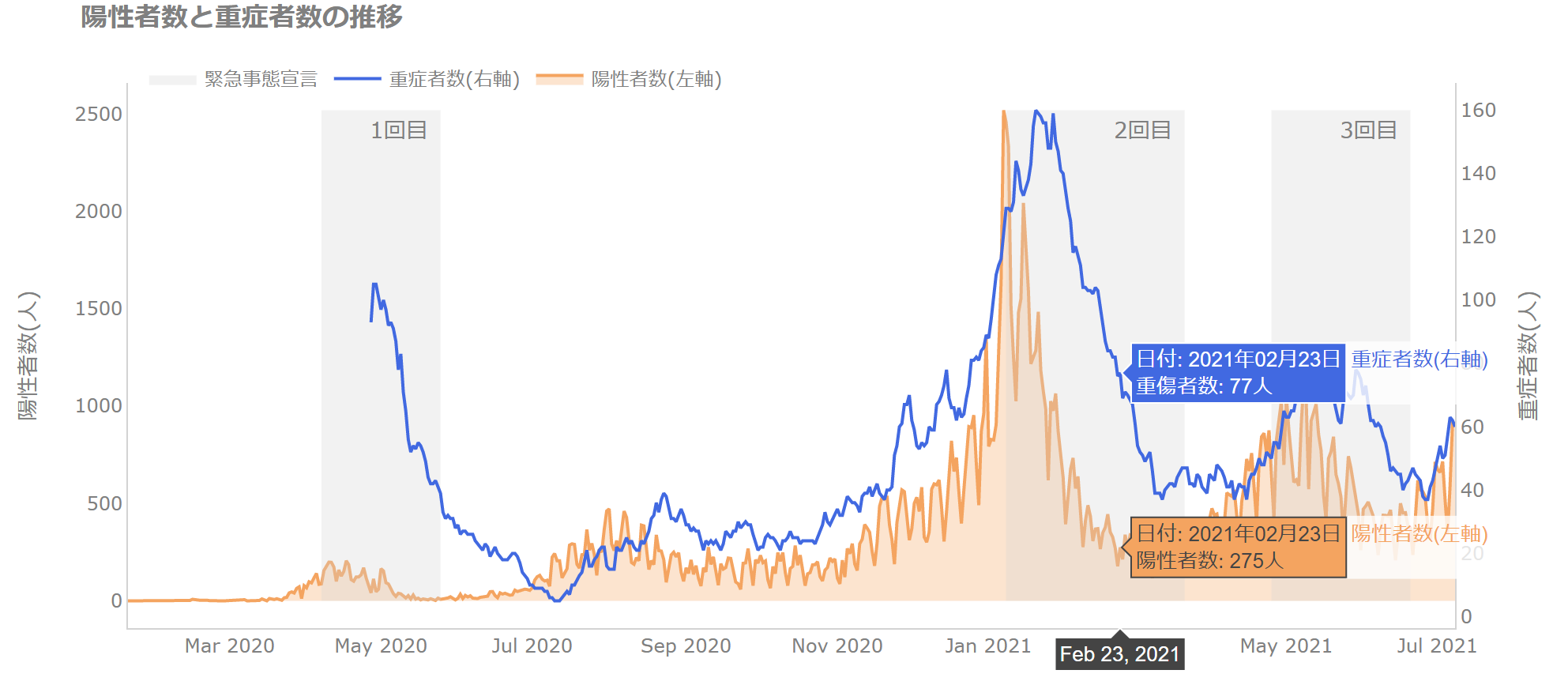
分析に関してもっと掘り下げるのであれば人流データなどを見れば、「宣言当初は人流が減っているけど途中から増加し始める」などの原因がわかるかもしれません(今さら感がありますがやってみたくなりますね)。
上記のグラフを作るためのコードも載せておきます。
少し大変ですので、自分が見るためだけであればここまでする必要はありません。
しかし、お客さんなどに見せる場合は、相手の認知負荷を下げるというのは非常に重要です。
まず、緊急事態宣言の期間を塗りつぶすための関数です。
from dateutil.relativedelta import relativedelta
def plot_state_of_emergency_term(fig, start_date, end_date, value, color, text, showlegend):
fig.add_trace(go.Scatter(x=[start_date]*2,
y=[0, value],
mode='lines',
line_width=0,
showlegend=False,
yaxis='y1')
)
fig.add_trace(go.Scatter(x=[end_date]*2,
y=[0, max_value],
mode='lines',
line_width=0,
fillcolor=color,
fill='tonexty',
showlegend=showlegend,
name='緊急事態宣言',
yaxis='y1')
)
fig.add_annotation(text=text,
align='left',
showarrow=False,
x=end_date-relativedelta(days=17),
y=max_value*0.96,
font=dict(color='grey',
size=14)
)
次に実際の描画部分です。
fig = go.Figure()
# 陽性者数のプロット
fig.add_trace(go.Scatter(x=df['日付'],
y=df['陽性者数'],
name='陽性者数(左軸)',
line_color='rgb(244, 164, 96)',
line_width=2,
fillcolor='rgba(244, 164, 96, 0.3)',
fill='tozeroy',
hovertemplate='日付: %{x|%Y年%m月%d日}<br>陽性者数: %{y}人',
yaxis='y')
)
# 重症者数のプロット
fig.add_trace(go.Scatter(x=df['日付'],
y=df['重症者数'],
name='重症者数(右軸)',
line_color='royalblue',
line_width=2,
hovertemplate='日付: %{x|%Y年%m月%d日}<br>重傷者数: %{y}人',
yaxis='y2')
)
# 緊急事態宣言1回目
plot_state_of_emergency_term(fig,
state_of_emergency_1_start,
state_of_emergency_1_end,
max_value,
'rgba(169, 169, 169, 0.3)',
'1回目',
showlegend=False,
)
# 緊急事態宣言2回目
plot_state_of_emergency_term(fig,
state_of_emergency_2_start,
state_of_emergency_2_end,
max_value,
'rgba(169, 169, 169, 0.3)',
'2回目',
showlegend=False,
)
# 緊急事態宣言3回目
plot_state_of_emergency_term(fig,
state_of_emergency_3_start,
state_of_emergency_3_end,
max_value,
'rgba(169, 169, 169, 0.3)',
'3回目',
showlegend=True,
)
fig.update_layout(yaxis1=dict(title='陽性者数(人)',
side='left'),
yaxis2=dict(title='重症者数(人)',
side='right',
overlaying='y',
showgrid=False),
hovermode="x"
)
fig.update_layout(title=dict(text='<b>陽性者数と重症者数の推移',
y=0.9),
showlegend=False,
plot_bgcolor='white',
font_color='grey',
width=1000,
)
fig.update_xaxes(showline=True,
linecolor='lightgrey',
linewidth=1,
color='grey')
fig.update_yaxes(showline=True,
linecolor='lightgrey',
linewidth=1,
color='grey')
fig.add_annotation(text='<b>重症者数',
showarrow=False,
font=dict(color='royalblue',
size=15),
x=datetime.date(2020, 5, 1),
y=1800)
fig.add_annotation(text='<b>陽性者数',
showarrow=False,
font=dict(color='rgb(244, 164, 96)',
size=15),
x=datetime.date(2020, 4, 1),
y=400)
fig.add_annotation(text='<b>緊急事態宣言',
showarrow=False,
font=dict(color='grey',
size=13),
x=datetime.date(2020, 3, 10),
y=2450)
2軸のプロットは避けたいという場合には、以下のようにするのも一つです。
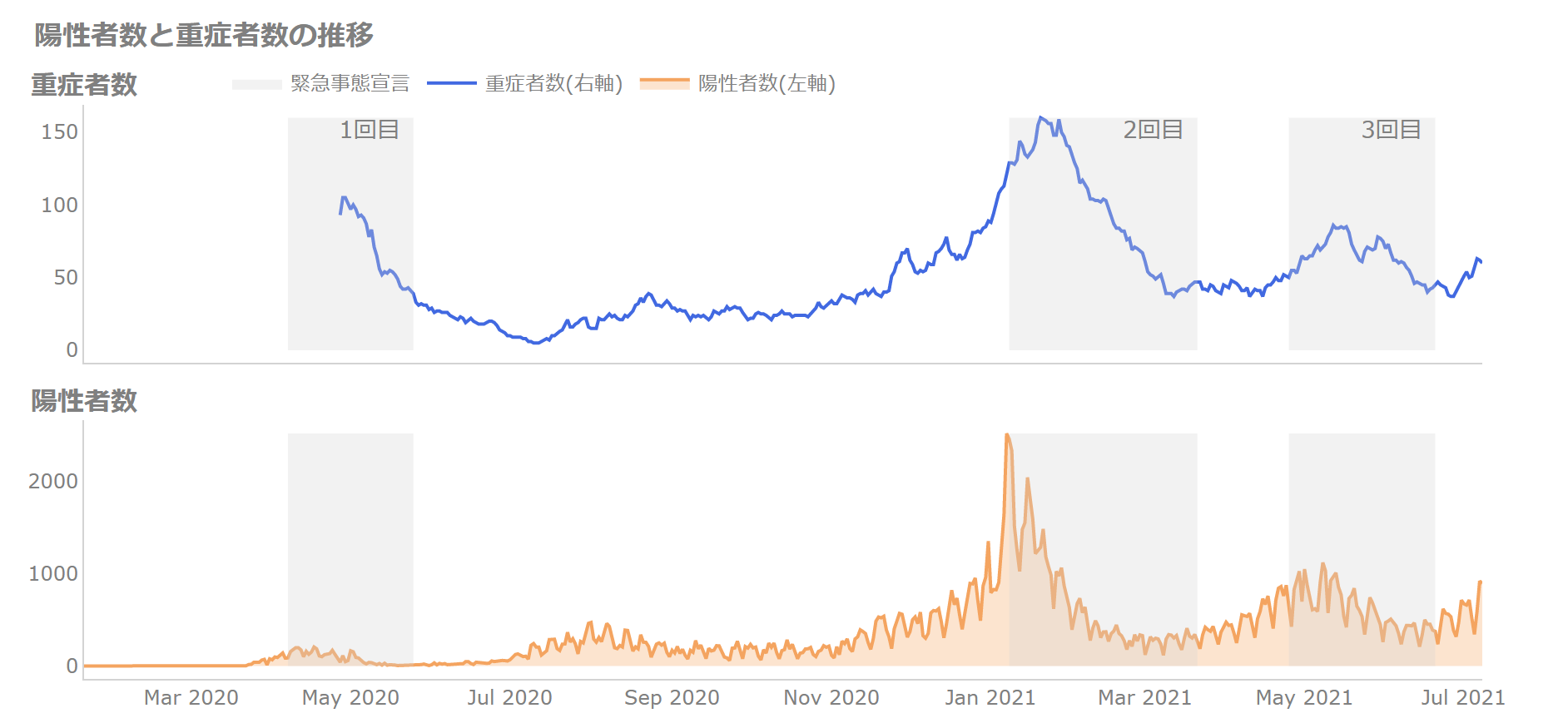
2軸のプロットは、どっちがどっちの軸かわかりにくい、左右を確認しないといけないという問題があるので、避けたいというのがあります(詳細はこちらで解説しています「【データ可視化】作ってはいけないグラフ6つ」)。
しかしながら、ラグがどれぐらいあるか?を見たい場合は前者の方が良いですね。
いずれにせよ、陽性者と重傷者の増減に明らかにラグがあることがわかりました(初めっからわかってるわ!というツッコミがありそうですが)。
コードはこちらです。
from dateutil.relativedelta import relativedelta
def plot_state_of_emergency_term_subplots(fig, start_date, end_date, value, color, text, showlegend, row, col):
fig.add_trace(go.Scatter(x=[start_date]*2,
y=[0, value],
mode='lines',
line_width=0,
showlegend=False,
),
row=row,
col=col
)
fig.add_trace(go.Scatter(x=[end_date]*2,
y=[0, value],
mode='lines',
line_width=0,
fillcolor=color,
fill='tonexty',
showlegend=showlegend,
name='緊急事態宣言',
),
row=row,
col=col
)
if row == 1:
fig.add_annotation(text=text,
align='left',
showarrow=False,
x=end_date-relativedelta(days=17),
y=value*0.95,
font=dict(color='grey',
size=14)
)
fig = make_subplots(rows=2, cols=1, shared_xaxes=True, subplot_titles=['<b>重症者数', '<b>陽性者数'],
vertical_spacing=0.1)
# 陽性者数のプロット
fig.add_trace(go.Scatter(x=df['日付'],
y=df['陽性者数'],
name='陽性者数(左軸)',
line_color='rgb(244, 164, 96)',
line_width=2,
fillcolor='rgba(244, 164, 96, 0.3)',
fill='tozeroy',
hovertemplate='日付: %{x|%Y年%m月%d日}<br>陽性者数: %{y}人',
),
row=2, col=1
)
# 重症者数のプロット
fig.add_trace(go.Scatter(x=df['日付'],
y=df['重症者数'],
name='重症者数(右軸)',
line_color='royalblue',
line_width=2,
hovertemplate='日付: %{x|%Y年%m月%d日}<br>重傷者数: %{y}人',
),
row=1, col=1
)
# 緊急事態宣言1回目
plot_state_of_emergency_term_subplots(fig,
state_of_emergency_1_start,
state_of_emergency_1_end,
max_value,
'rgba(211, 211, 211, 0.3)',
'1回目',
showlegend=False,
row=2, col=1
)
# 緊急事態宣言2回目
plot_state_of_emergency_term_subplots(fig,
state_of_emergency_2_start,
state_of_emergency_2_end,
max_value,
'rgba(211, 211, 211, 0.3)',
'2回目',
showlegend=False,
row=2, col=1
)
# 緊急事態宣言3回目
plot_state_of_emergency_term_subplots(fig,
state_of_emergency_3_start,
state_of_emergency_3_end,
max_value,
'rgba(211, 211, 211, 0.3)',
'3回目',
showlegend=False,
row=2, col=1)
# 緊急事態宣言1回目
plot_state_of_emergency_term_subplots(fig,
state_of_emergency_1_start,
state_of_emergency_1_end,
max_value_2,
'rgba(211, 211, 211, 0.3)',
'1回目',
showlegend=False,
row=1, col=1
)
# 緊急事態宣言2回目
plot_state_of_emergency_term_subplots(fig,
state_of_emergency_2_start,
state_of_emergency_2_end,
max_value_2,
'rgba(211, 211, 211, 0.3)',
'2回目',
showlegend=False,
row=1, col=1
)
# 緊急事態宣言3回目
plot_state_of_emergency_term_subplots(fig,
state_of_emergency_3_start,
state_of_emergency_3_end,
max_value_2,
'rgba(211, 211, 211, 0.3)',
'3回目',
showlegend=True,
row=1, col=1)
fig.update_layout(title=dict(text='<b>陽性者数と重症者数の推移',
y=0.9),
plot_bgcolor='white',
font_color='grey',
legend=dict(x=0.1,
y=1.08,
orientation='h'),
hovermode='x',
width=1000,
)
fig.update_xaxes(showline=True,
linecolor='lightgrey',
linewidth=1,
color='grey')
fig.update_yaxes(showline=True,
linecolor='lightgrey',
linewidth=1,
color='grey')
fig.layout.annotations[0].x = 0
fig.layout.annotations[1].x = 0
fig.show()
あと、やはり曜日による変動がありますね。
それを除くために、1週間ごとの陽性者合計と、重傷者の平均に変換しましょう。
すると以下のようになります。
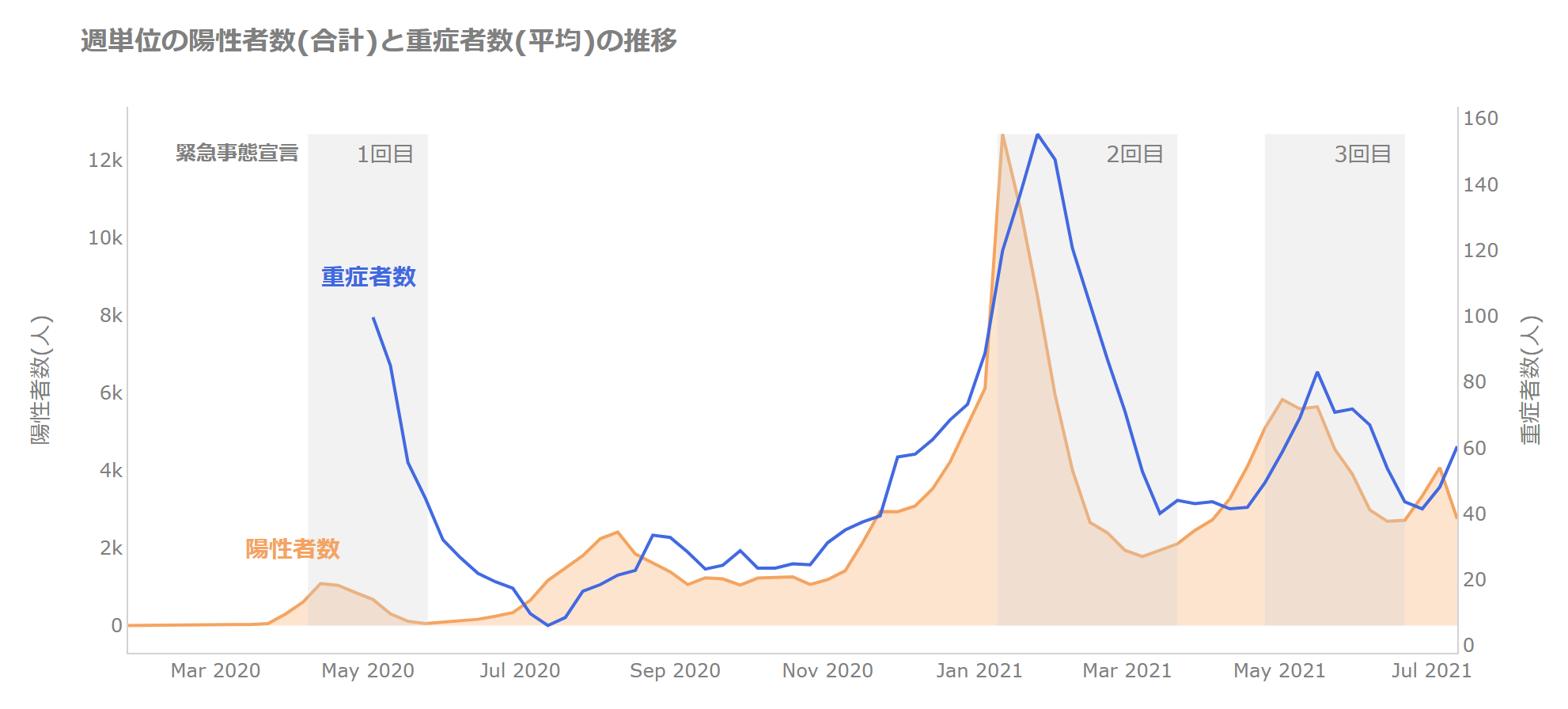
では、差について見ていきましょう。
2軸のプロットを使わないバージョンでは、以下のようになっています。
なかなか差になるとパッとはわかりにくいかもしれませんね。
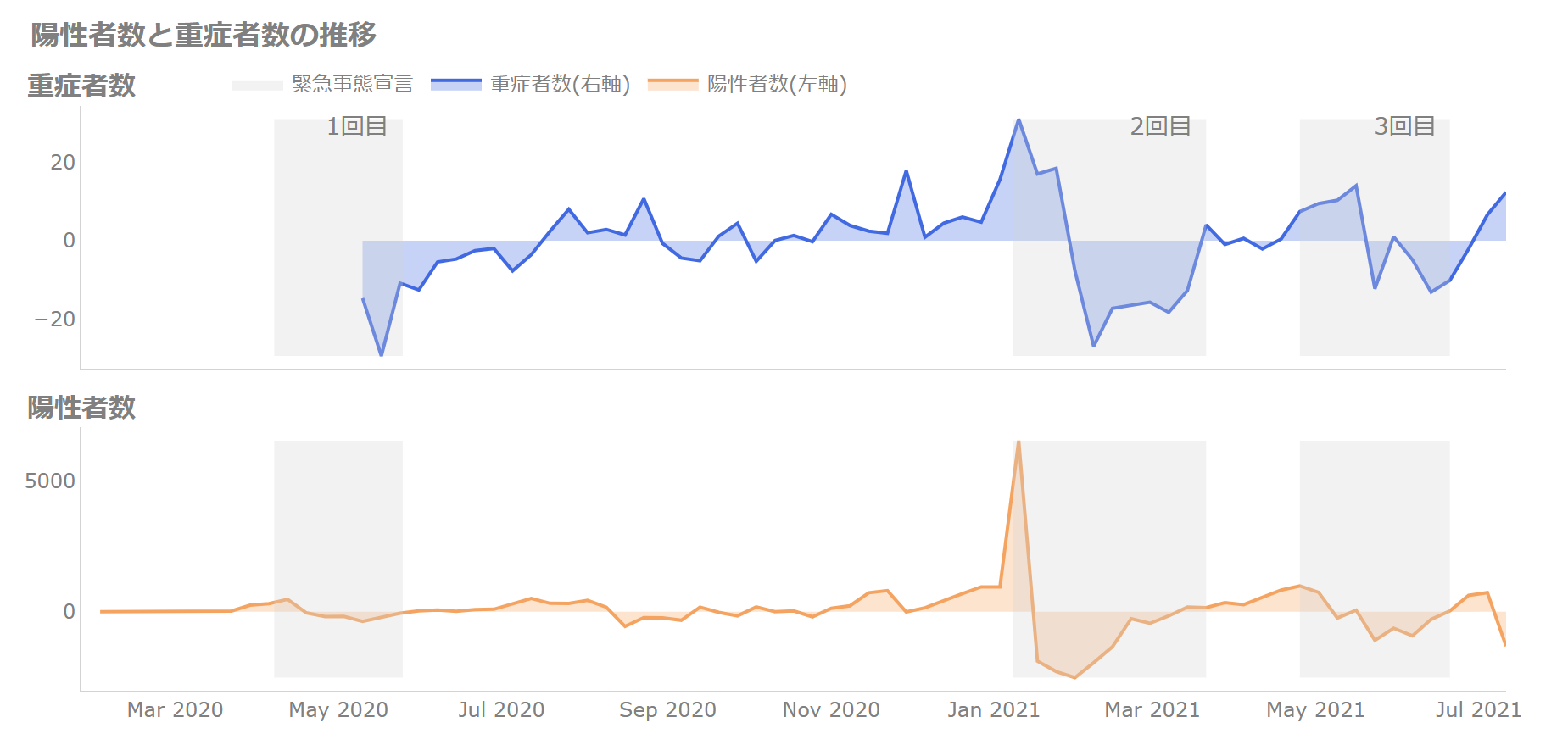
統計量の見る
では、ラグを取って相関係数を計算してみましょう。
それにより、陽性者数の増減と重傷者数の増減にどれぐらいのラグがあるか何となくわかりますね。
ラグと相関係数の関係は以下のようになりました。
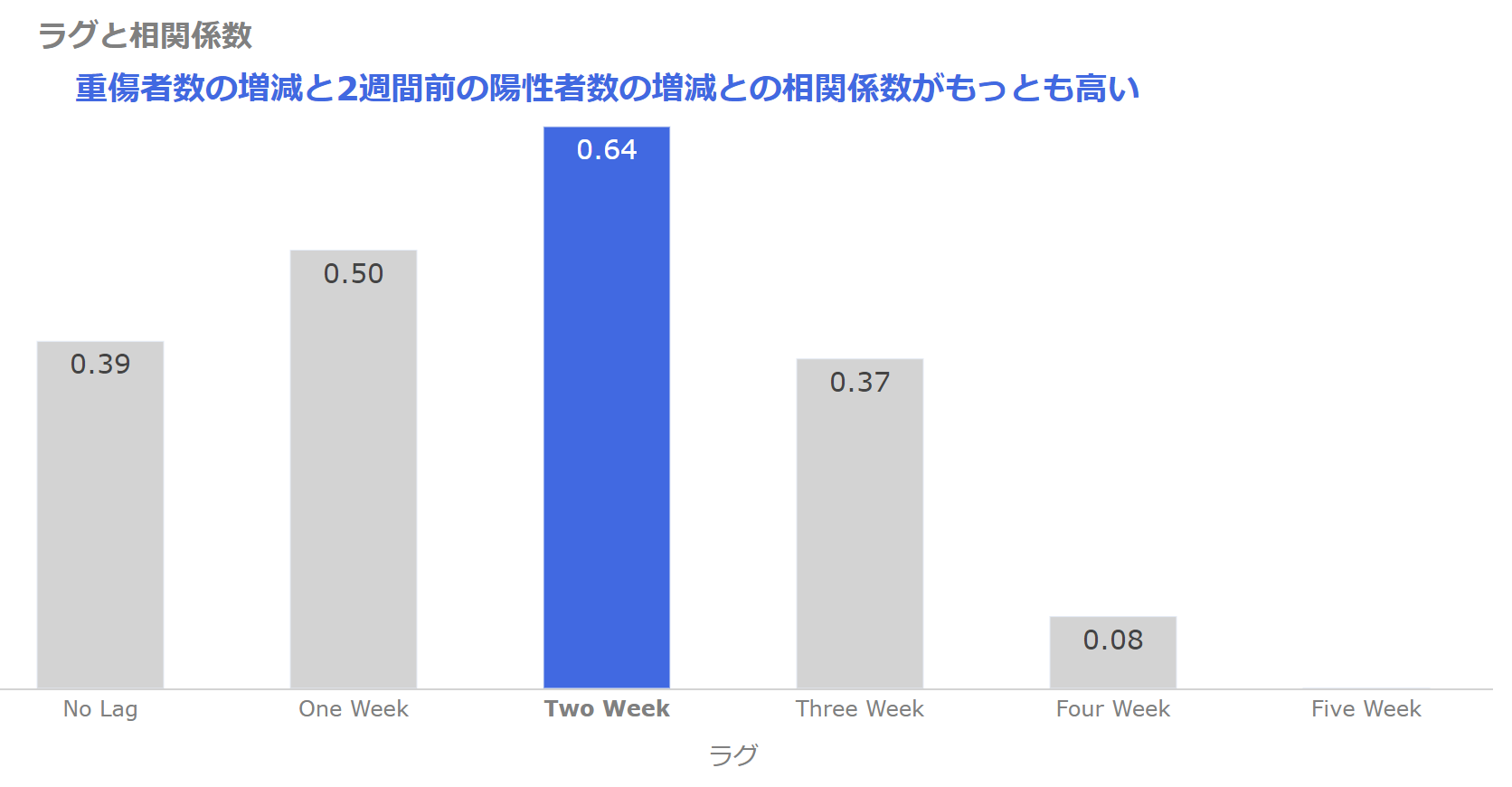
重要なポイントは相関係数の値と、相関係数が一番大きくなっているところなので、数値をグラフに直接表示し、Two Weekのところを色を変えて強調します。
また、図に直接コメントを描くことで、伝えたい内容がすぐにわかります。
2週間のラグを取った場合の相関係数が一番高くなってますね。
ラグがゼロの場合も相関係数が高くなっていますが、陽性者数や重傷者数が増加し始めると、当分の間増加する、もしくは減少し始めると当分の間減少する、というトレンドがあるからですね。
さらに差の差を取るとトレンドが取り除けて、ラグがない場合などの相関係数が小さくなります。
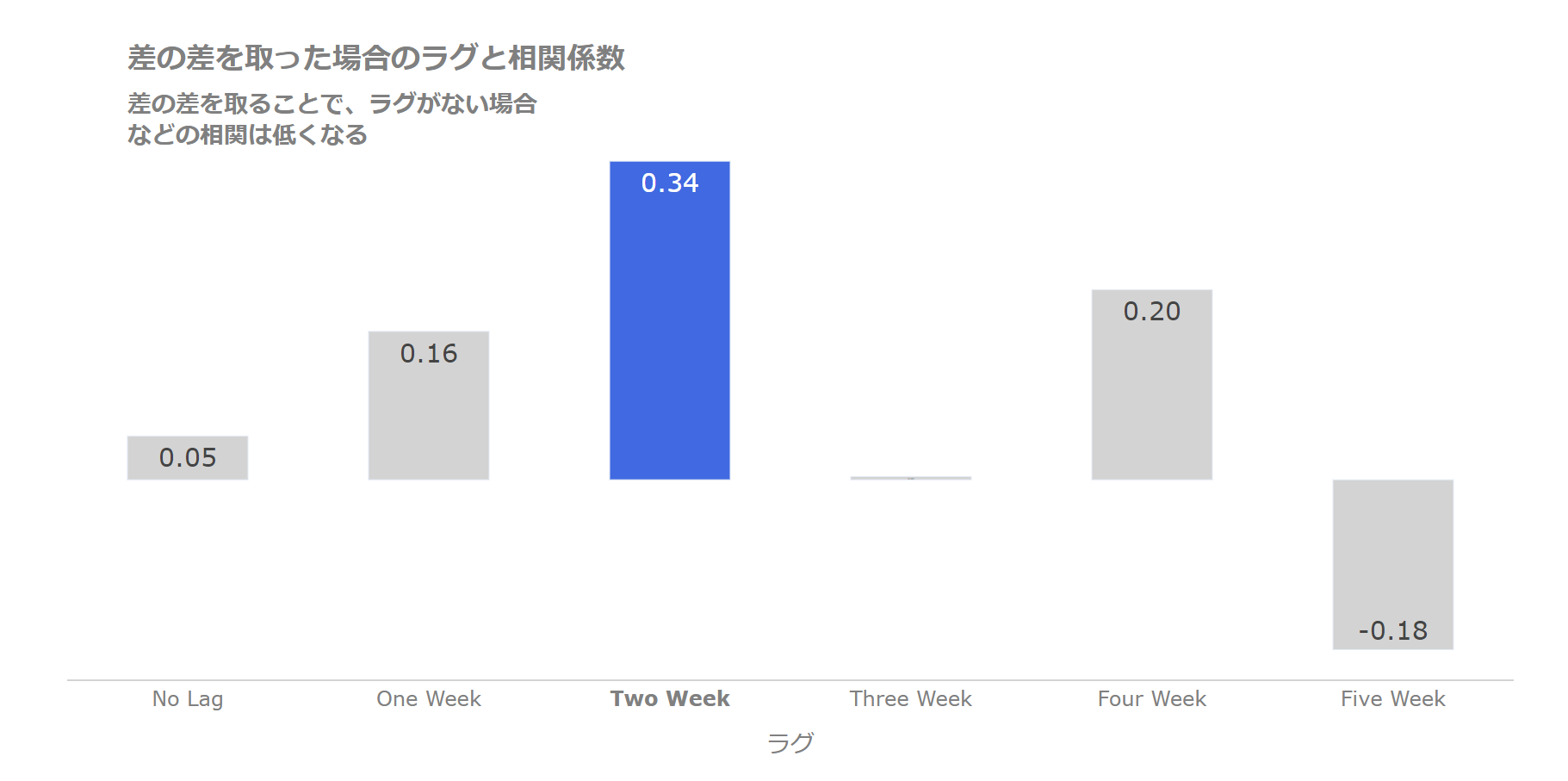
いずれにせよ、2週間前の陽性者の増減との相関がもっとも高くなっています。
では、ここで散布図を描いて、実際のデータを見てみましょう。
重要なのは、相関係数などの集約された統計量だけを見るのではなく、かならずデータ自体を見ると言うことです。
ここは自分でデータを確認するだけなので、いったん雑に見てみましょう。
fig = make_subplots(rows=2, cols=3, shared_xaxes='all', shared_yaxes='all',
subplot_titles=['no lag', 'one week', 'two week', 'three week', 'four week', 'five week'])
for i, column_name in enumerate(column_names):
row, col = divmod(i, 3)
row += 1
col += 1
fig.add_trace(go.Scatter(x=df_week_diff['陽性者数'],
y=df_week_diff[column_name],
mode='markers',
marker_color='royalblue',
text=df_week_diff.index),
col=col, row=row
)
fig.update_layout(showlegend=False)
fig.update_xaxes(title='陽性者数増減', col=1, row=2)
fig.update_xaxes(title='陽性者数増減', col=2, row=2)
fig.update_xaxes(title='陽性者数増減', col=3, row=2)
fig.update_yaxes(title='重症者数増減', col=1, row=1)
fig.update_yaxes(title='重症者数増減', col=1, row=2)
fig.show()
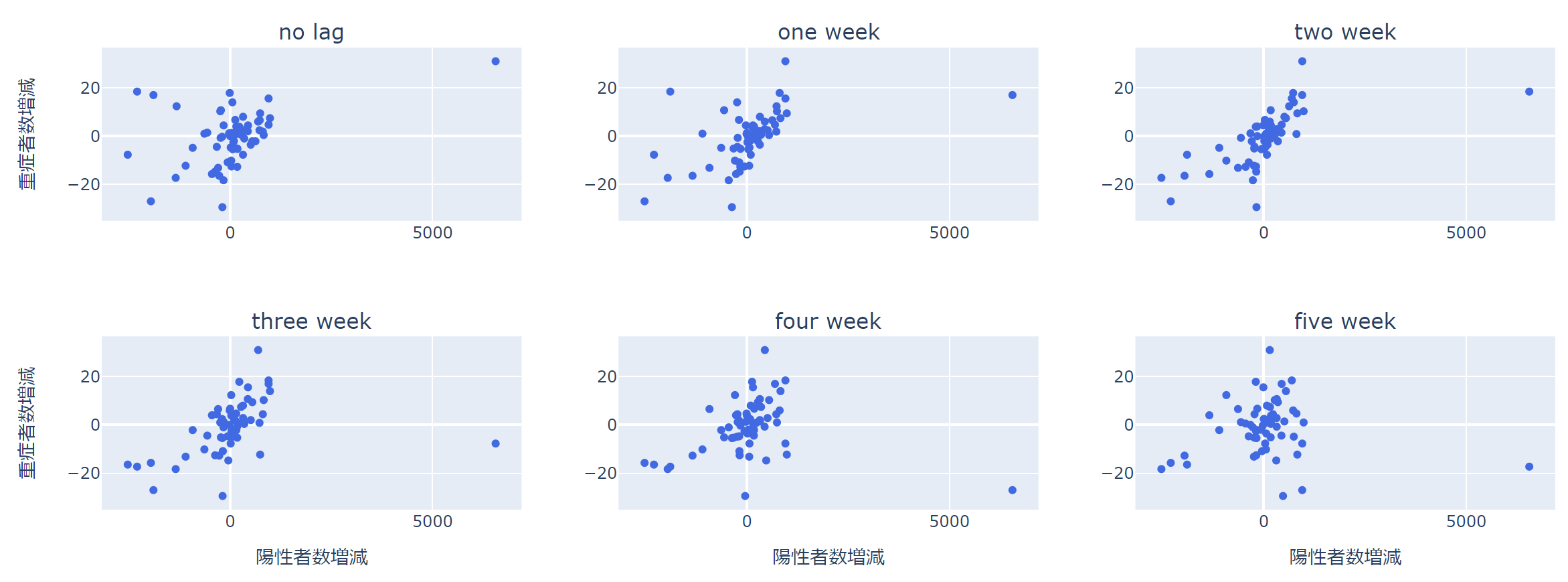
大きく外れた値がありますね。
どんな時期なのか確認しましょう。
textに日付を渡しておくことで、カーソルを当てれば日付を確認することができます。
ここでは、書式はキレイにしていませんが、2021年1月10日ということはわかります。
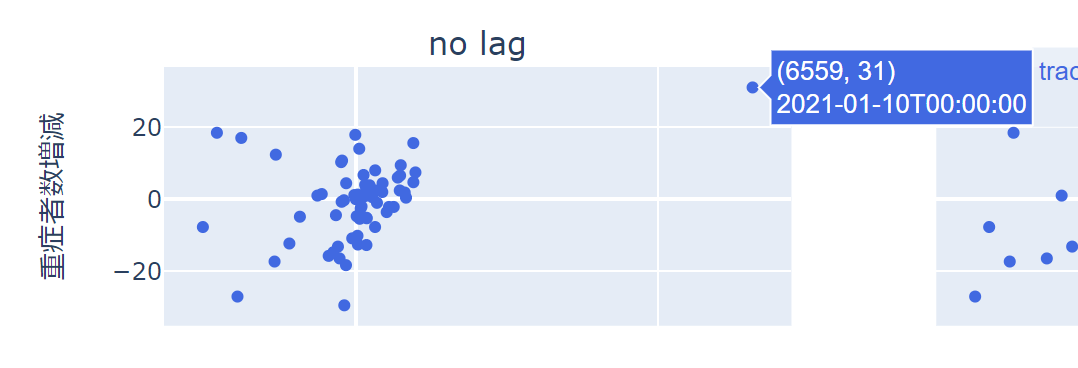
2回目の緊急事態宣言の陽性者数が大幅に増えた時期ですね。
では、これを除いて見てみましょう。
インタラクティブな散布図で嬉しいのは、注目したい部分を拡大したり、除きたい部分を簡単に取り除けることです。
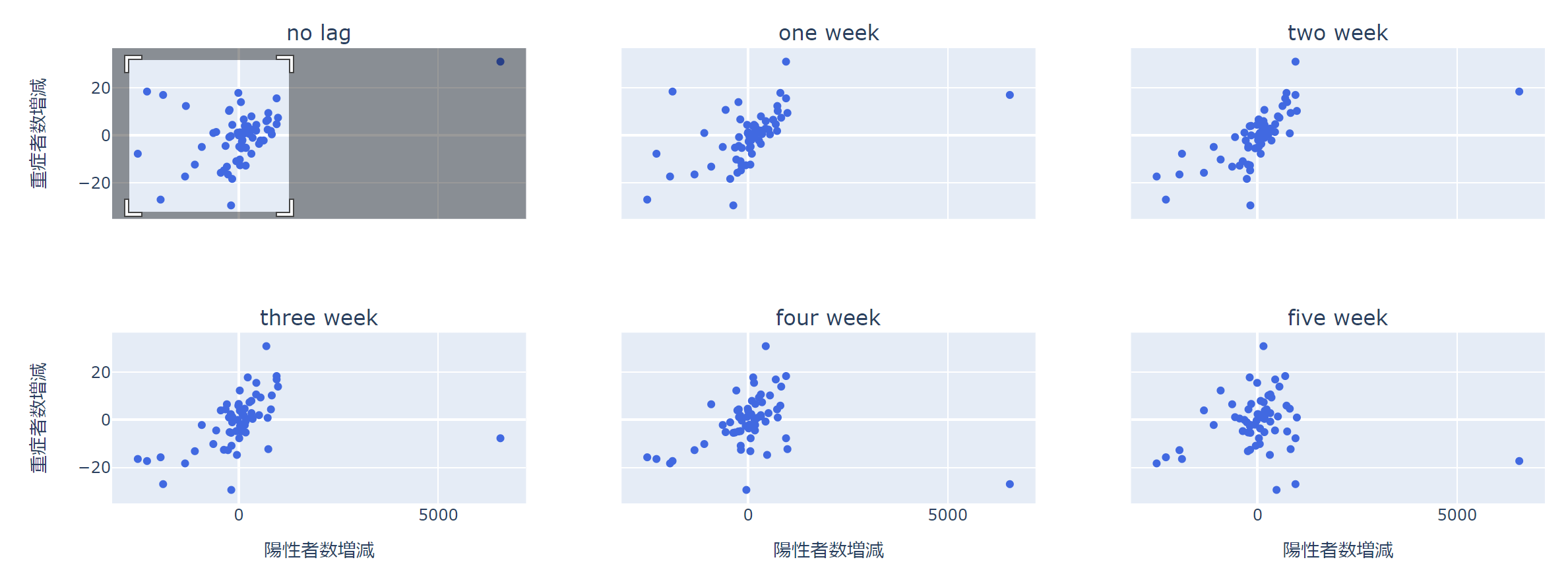
すると、shared_xaxes、shared_yaxesを"all"に設定していることから、すべてのサブプロットについて、範囲が同時に変わります。
ラグなしの左上の図では、1点を除くとだいぶ違った見た目になります。
相関係数は1点や数点の影響で大きく出たり小さく出たりすることがあるので、かならず散布図で分布を確認しましょう。
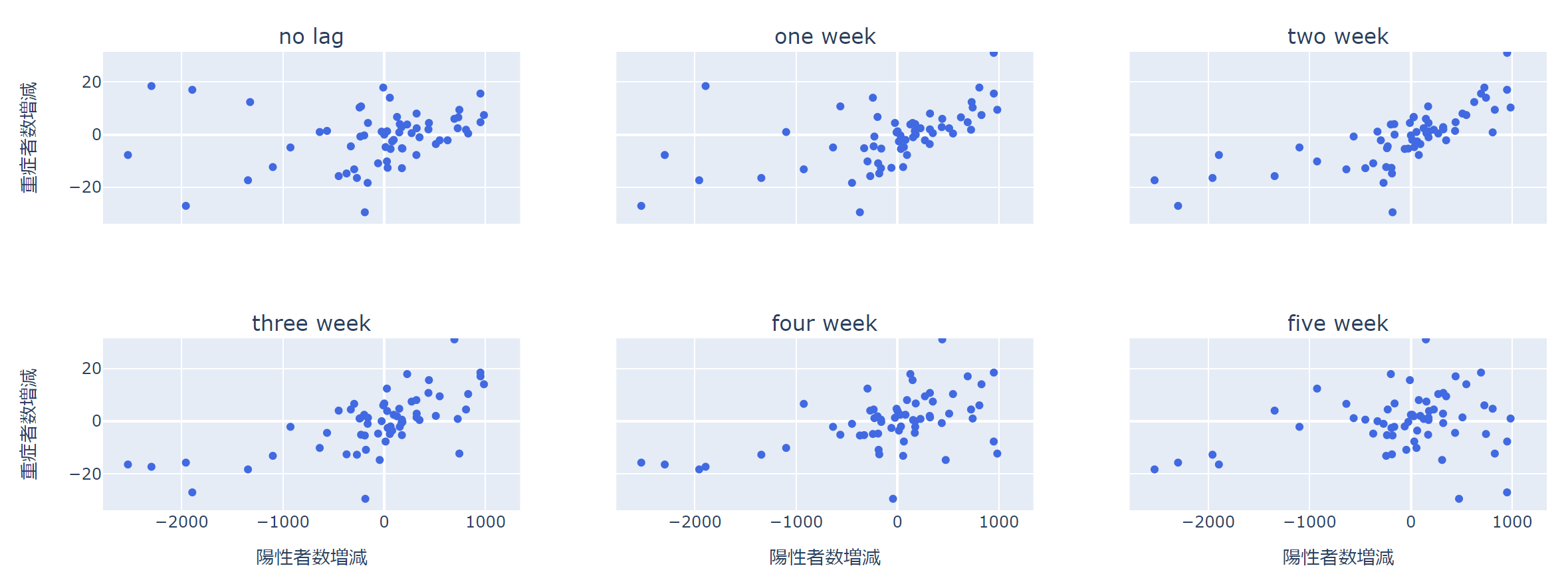
ということで、これから行う回帰については2021年1月10日の週は除いて行います。
回帰モデルの作成
では、簡単に回帰モデルを作成しましょう。
statsmodelsのapiをインポートします(sklearnを使ってもいいです)。
import statsmodels.api as sm
説明変数と目的変数をセットします。
x = df_week_diff.dropna(subset=['陽性者数', 'shift_2w'])['陽性者数'] X = sm.add_constant(x) y = df_week_diff.dropna(subset=['陽性者数', 'shift_2w'])['shift_2w']
ここでは一応、切片項も入れておきます。
ただ、切片項が有意になってしまうと、陽性者数が増減しないのに重傷者数が増減することになるので、モデルとしてはよくありませんね。
では、回帰をしましょう。
model = sm.OLS(y, X) results = model.fit() print(results.summary())
結果は以下の通りです。
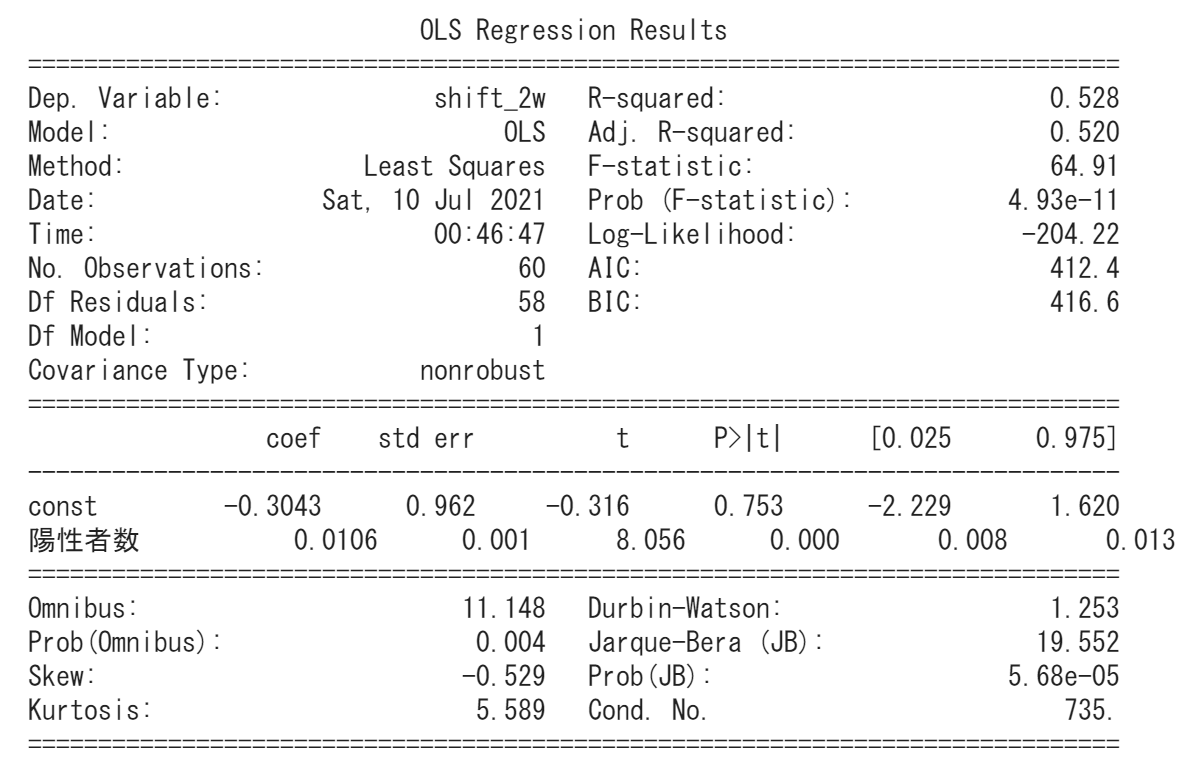
と言っても、これではわかりませんので、係数関係をまとめました。
| 係数 | 標準誤差 | t値 | p値 | |
|---|---|---|---|---|
| 切片 | -0.3043 | 0.962 | -0.316 | 0.753 |
| 陽性者数増減 | 0.0106 | 0.001 | 8.056 | 0.008 |
切片項については、係数が-0.3ですがp値が75.3%ということで有意ではなさそうですね。
常識と合っている結果ですね。
ちなみに、決定係数は0.535となっています。
ということで、切片を抜いて回帰しましょう。
結果は以下のようになります。
| 係数 | 標準誤差 | t値 | p値 | |
|---|---|---|---|---|
| 陽性者数増減 | 0.0106 | 0.001 | 8.205 | 0.000 |
p値が0.0%なので十分有意なようですね。
係数は0.0106ということで、1週間の新規陽性者数が前週比100人増えると1人重傷者が増えるという結果になります。
1週間で前週より5000人の新規陽性者が増えた場合(前週比なので+5000人はかなり急激な増加になります)、53人重傷者が増えることになります。
個人的な思いはありますが、それが多いか少ないかは読者の皆様にお任せします(笑)
一応、非線形になっているように見えるので、陽性者数増減の2乗の項も入れて、重回帰をしてみましょう。
| 係数 | 標準誤差 | t値 | p値 | |
|---|---|---|---|---|
| 陽性者数増減 | 0.0143 | 0.002 | 8.072 | 0.000 |
| 陽性者数増減**2 | 2.79E-06 | 9.73E-07 | 2.864 | 0.006 |
ともに係数は有意なようです。
自由度調整済み重決定係数は0.577です。
グラフにするとこのようになります(コードは次の図のときに記載します)。
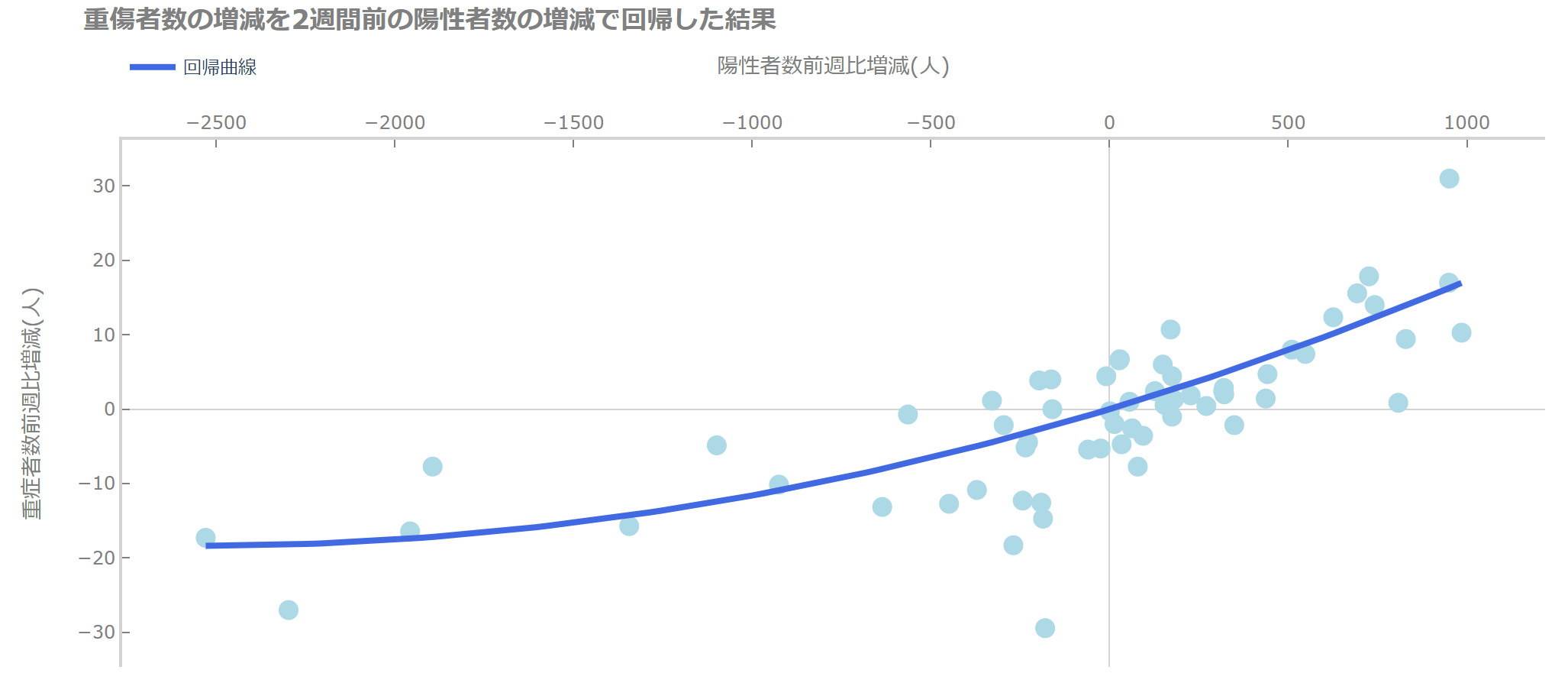
では、少し気になっている最近は高齢者のワクチン接種が進んできたので新規陽性者数が増えても重傷者数がそれほど増えないのではないか?という素朴な疑問を確認してみましょう。
期間を2021年3月より前と後で分けて、前半部分のデータで先ほどと同じように重回帰を行います。
そして、グラフを使って傾向を見比べてみましょう。
まず、こちらで重回帰を行います。
x_1st = X.loc[:'2021-3-31'] y_1st = y.loc[:'2021-3-31'] x_2nd = X.loc['2021-4-01':] y_2nd = y.loc['2021-4-01':] model = sm.OLS(y_1st, x_1st) results = model.fit() print(results.summary())
では、グラフを作成しましょう。
念のためですが、回帰した結果を表示するためのデータはこのように作成しています。
x_lin = np.linspace(X['陽性者数'].min(), X['陽性者数'].max(), 100) x_lin = x_lin.reshape(-1, 1) x_lin = np.concatenate([x_lin, x_lin ** 2], axis=1) predicted = results.predict(x_lin)
では、結果を見てみましょう。
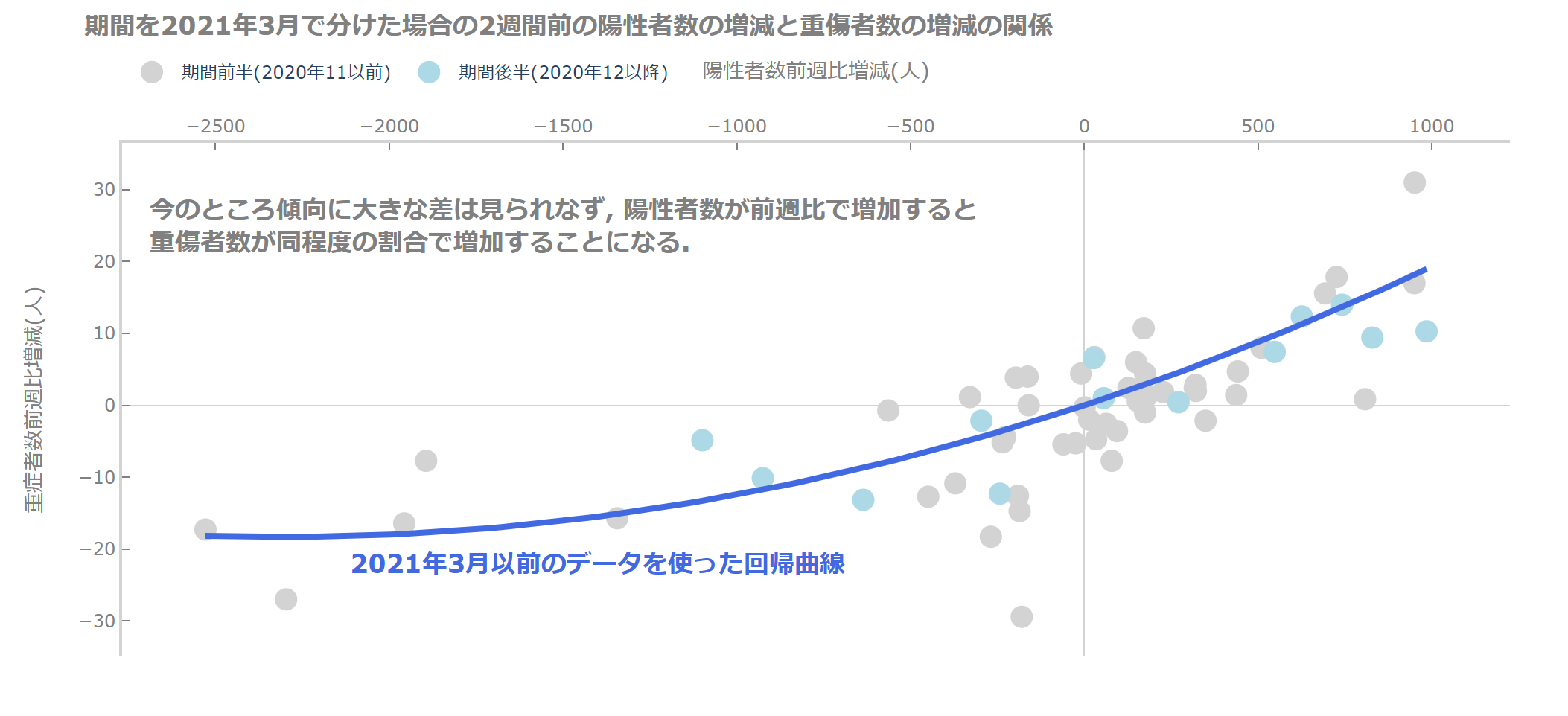
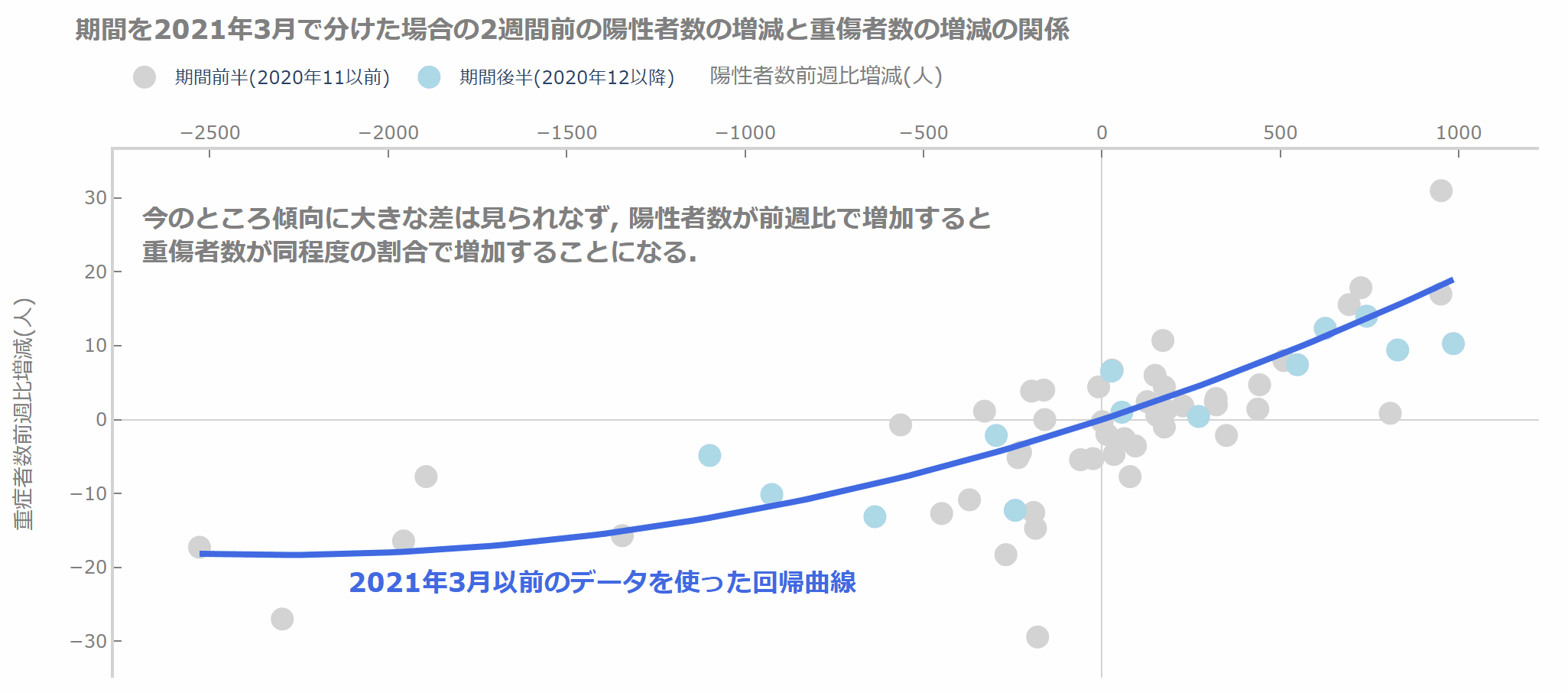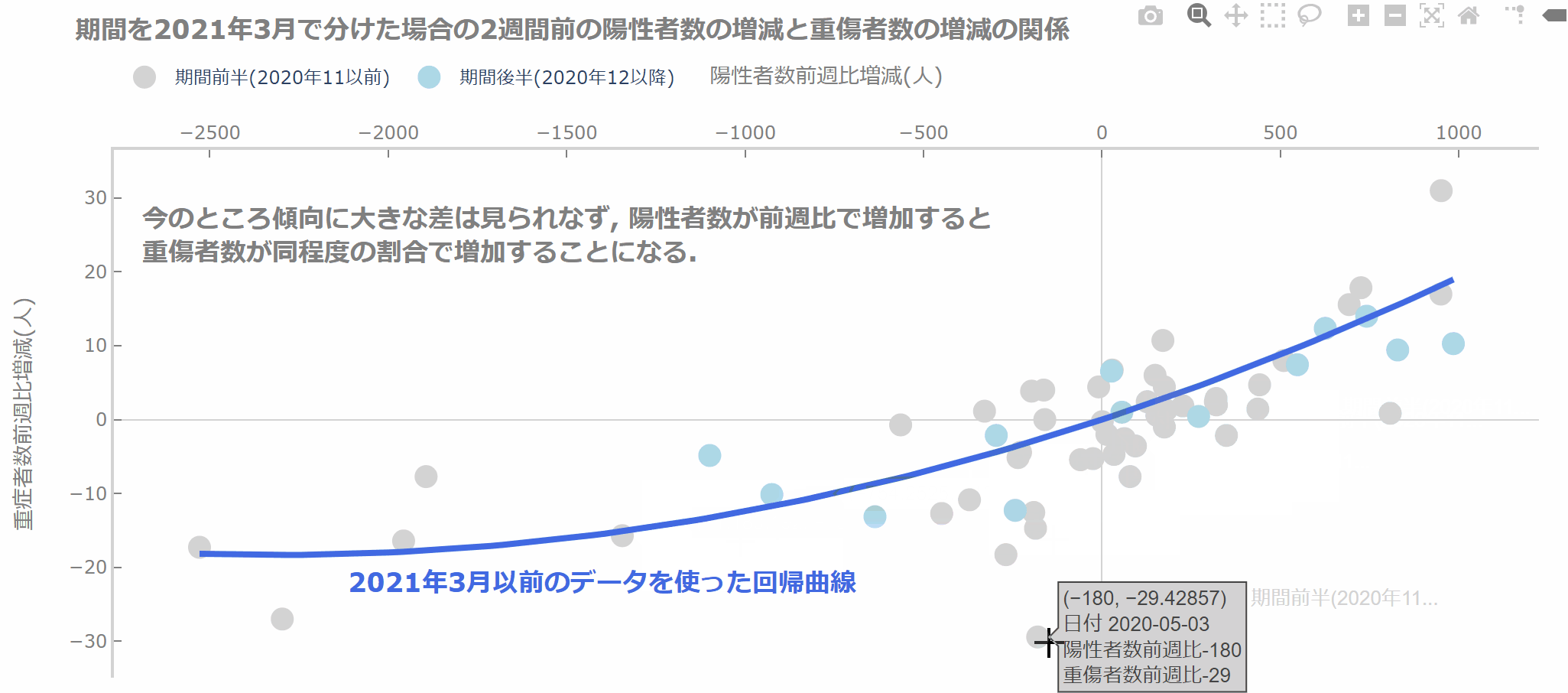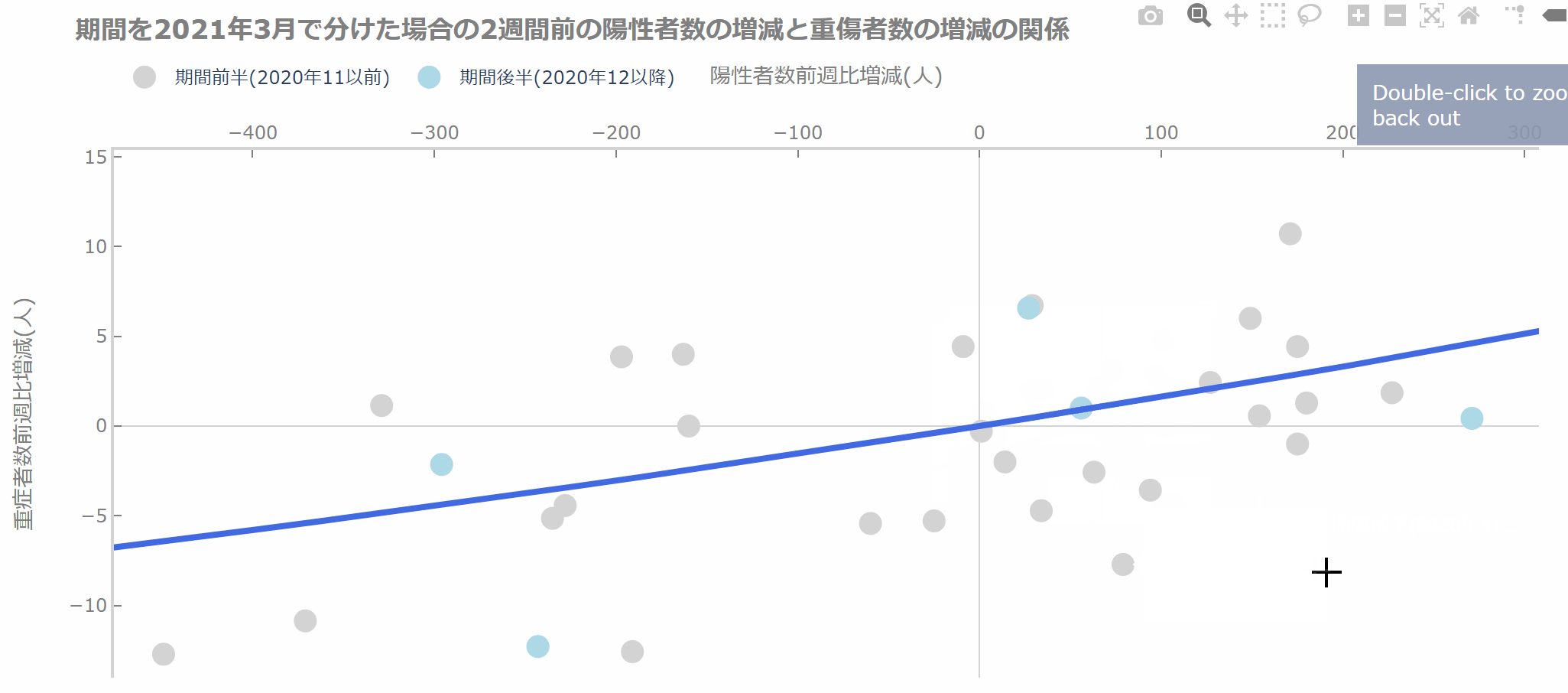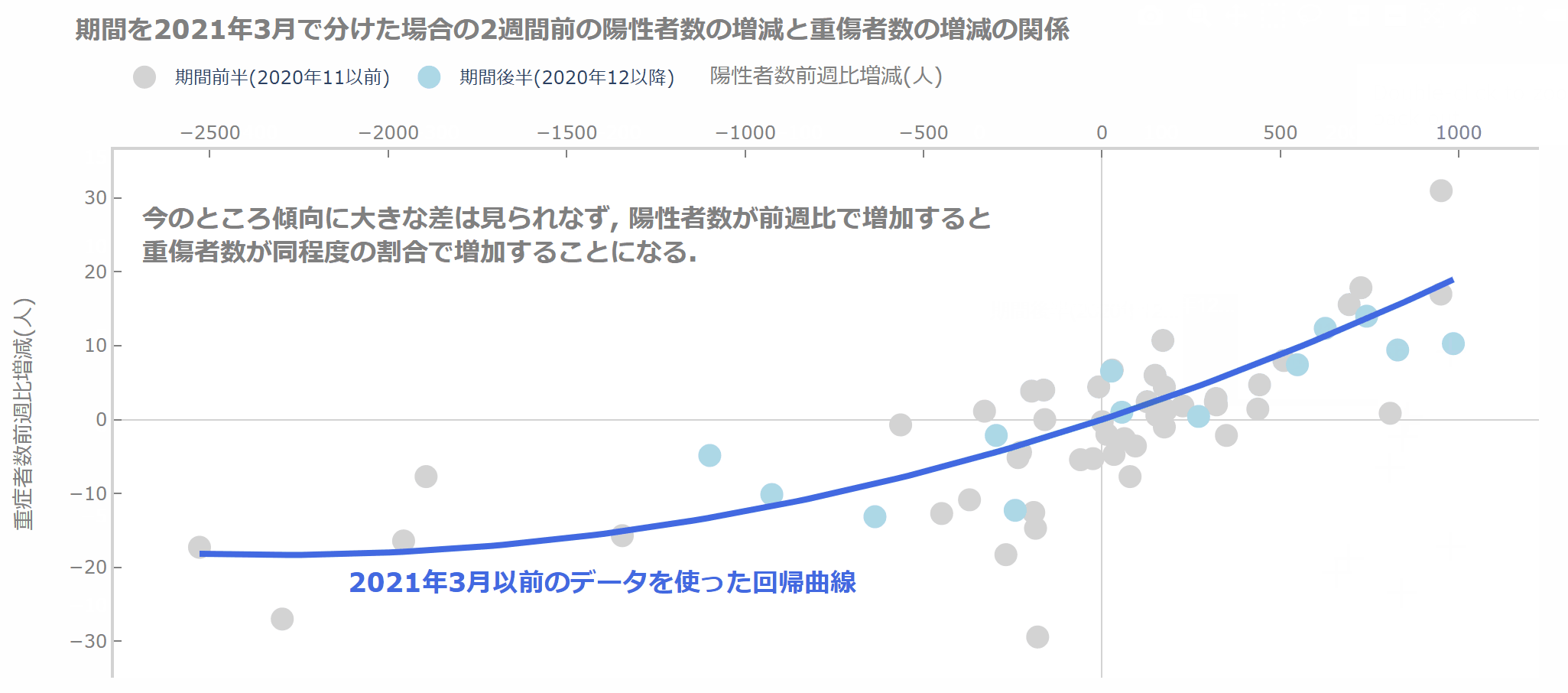
今のところ、2021年3月以前とそれ以降で傾向はそれほど変わりませんね。
これから変わってくるのかもしれません(と期待しています)。
汚いですが、一応コードも載せておきます。
fig = go.Figure()
text = [f'日付{idx: %Y-%m-%d}<br>陽性者数前週比{int(x["陽性者数"]):+d}<br>'+
f'重傷者数前週比{int(y["shift_2w"]):+d}' for (idx, x), (_, y) in zip(x_1st.iterrows(), y_1st.iterrows())]
fig.add_trace(go.Scatter(x=x_1st['陽性者数'],
y=y_1st['shift_2w'],
mode='markers',
name='期間前半(2020年11以前)',
marker=dict(color='lightgrey',
size=15),
text=text
))
text = [f'日付{idx: %Y-%m-%d}<br>陽性者数前週比{int(x["陽性者数"]):+d}<br>'+
f'重傷者数前週比{int(y["shift_2w"]):+d}' for (idx, x), (_, y) in zip(x_2nd.iterrows(), y_2nd.iterrows())]
fig.add_trace(go.Scatter(x=x_2nd['陽性者数'],
y=y_2nd['shift_2w'],
mode='markers',
name='期間後半(2020年12以降)',
marker=dict(color='lightblue',
size=15),
text=text
))
fig.add_trace(go.Scatter(x=x_lin[:, 0],
y=predicted,
mode='lines',
line_color='royalblue',
line_width=4,
name='回帰曲線',
showlegend=False
))
fig.update_layout(title=dict(text='<b>期間を2021年3月で分けた場合の2週間前の陽性者数の増減と重傷者数の増減の関係',
font_color='grey',
font_size=17,
y=0.97
),
plot_bgcolor='white',
showlegend=True,
legend=dict(orientation='h',
x=0,
y=1.18)
)
fig.update_xaxes(title=dict(text='陽性者数前週比増減(人)',
),
showline=True,
linewidth=2,
linecolor='lightgrey',
color='grey',
side='top',
zeroline=True,
zerolinewidth=1,
zerolinecolor='lightgrey',
tickson='boundaries',
ticks='inside',
ticklen=5)
fig.update_yaxes(title='重症者数前週比増減(人)',
showline=True,
linewidth=2,
linecolor='lightgrey',
color='grey',
zeroline=True,
zerolinewidth=1,
zerolinecolor='lightgrey',
tickson='boundaries',
ticks='inside',
ticklen=5
)
fig.add_annotation(text='<b>今のところ傾向に大きな差は見られなず, 陽性者数が前週比で増加すると<br>重傷者数が同程度の割合で増加することになる.',
showarrow=False,
align='left',
x=-1500,
y=25,
font=dict(size=17,
color='grey'))
fig.add_annotation(text='<b>2021年3月以前のデータを使った回帰曲線',
showarrow=False,
align='left',
x=-1400,
y=-22,
font=dict(size=17,
color='royalblue'))
fig.show()
インタラクティブに動かしている様子はこちらです。
まとめ
今回の分析はこれぐらいにしておきましょう。
ちゃんとやろうと思えば分布の比較のための検定をしたりとか色々ありますが、ここでの主題はあくまでもplotlyを使ったデータの可視化、分析方法のご紹介なので、これぐらいにしておきましょう。
まだまだ気になる方は、簡単にデータは取ってこれるのでやってみてください。
その際は、せっかくなのでplotlyを使っていただけると嬉しいです。
あと、個人的には楽しくてやりすぎてしまう傾向がありますが、あまりレイアウトを設定するのに時間を掛けるのもよくないので、皆さまはほどほどにしましょう。
ここでは、詳しいコードの説明はしていませんので、以下の投稿を参考にしていただければと思います。
では、また違ったデータで遊んでみたいと思います!



